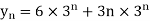Unit - 2
Z-Transforms
Q1) Find the z-transform of the signal x(n) = sin w0n u(n) and find ROC.
A1) X(z) = 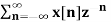
X(z) = 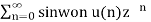
= 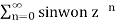 sin
sin 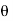 = ej
= ej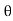 - e-j
- e-j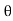 / 2j
/ 2j
= 1/2j 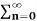 (ejw0n – e –jwon )z-n
(ejw0n – e –jwon )z-n
= 1/2j 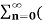 ejwon z-1) n -
ejwon z-1) n - 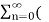 e-jw0z-1) n
e-jw0z-1) n
1/2j[ 1/1-ejw0z-1 – 1/1-e-jw0z-1]
= sin w0 z-1/ 1-2cos(wo)z-1 + z-2 ROC |z| >1
Q2) Find the z-transform of the sequence x(n) = a n-1 u(n-1)
A2) We know that x(n) = an u(n) is
X(z) = 1/1/az-1
By using time shifting property we have Z{ x(n-k)} = z-k X(z)
Therefore
Z{an-1 u(n-1)} = z-1/ 1-az-1 = 1/z-a. ROC |z| > |a|
Q3) Find the z-transform of the sequence x(n) = an cos nπ/2
A3) Z{ cos w0n} = 1- (cos w0) z-1/ 1 –(2 cos w0) z-1 + z-2
Since w0=π/2
Z{ cos π/2 n u(n)} = 1/1 + z-2
Using exponential sequence property
Z{ an x(n) } = X(a-1 z)
Z{ an cos nπ/2} = 1/1+(a-1z)-2 = 1/ 1 + a2/z2 = z2/ a2 + z2
Q4) Find the z transform of the sequence x(n) = n u(n)
A4) The z-transform of unit step sequence is given by
Z{u(n)} = z/z-1
Z{ n u(n)} = -z d/dz (z/z-1)
= z/(z-1)2
Q5) If x(n) = x1(n) * x2(n) where x1(n) = (1/3)n u(n) and x2(n) = (1/5)n u(n). Find X(z) by using convolution property.
A5) X1(z) = 1/ 1- (1/3)z-1 X2(z) = 1/1- (1/5) z-1
X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1
Using z-transform find the convolution of two sequences.
x1(n) = {1,2,-1,0,3} x2(n) = { 1,2,-1}
Z{ x1(n) * x2(n)} = X1(z) . X2(z)
X1(z) = 1 + 2z-1 – z-2 + 3 z-4
X2(z) = 1 + 2z-1 – z-2
(1 + 2z-1 – z-2 + 3 z-4 ) (1 + 2z-1 – z-2 )
= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6
Q6) Determine the z-transform of the signal x(n ) = rn (sin w0n ) u(n)
A6) Z{(sin w0n ) u(n)} = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2
Z{an x(n)} = X(a-1 z)
Therefore
Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2
= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2
Q7) Determine the signal x(n) whose z-transform is given by X(z) = log(1- az-1).
A7) X(z)= log(1-az-1)
Differentiating both side we get
d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1
-z d/dz { X(z)} = -az-1/1-az-1
= -az-1[ 1/1-az-1]
= -a Z[ a n-1 u(n-1)] -------- (1)
From differentiation property
Z{ n x(n)} = -z d/dz [ X(z)] ------- (2)
Comparing (1) and (2) we get
n x(n) = -a [ a n-1 u(n-1)]
Or x(n) = -a [a n-1 u(n-1)]/n
Q8) Determine the z-transform of the signal x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)
A8) x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)
=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)
We know that
Z[(1/3) n u(n)] = z/ z-1/3
Using time-shifting property
Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3
Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]
=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2
Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]
= z(z+1/3)/(z-1/3)2
= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4
= z(z+1/3)/(z-1/3)3
X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]
= z2/(z-1/3)3
Q9) Find the z-transform for the sequence x[n] = 2 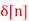 + 3
+ 3 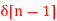 + 5
+ 5 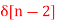 + 2
+ 2 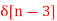
A9)
X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3
Q10) Find the z-transform and ROC of the signal x(n) = an u(n)
A10) X(z) = 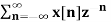
= 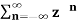 an u(n) -----(1) u(n) = 0 for n<0
an u(n) -----(1) u(n) = 0 for n<0
1 for n≥0
= 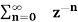 an ------- (2)
an ------- (2)
= 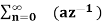 n ------- (3)
n ------- (3)
This is a geometric series of infinite length that is
a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1
Then from equation (3) it converges when |az-1| < 1 or |z| >|a|
Therefore
X(z) = 1/ 1-az-1: ROC |z| > |a|
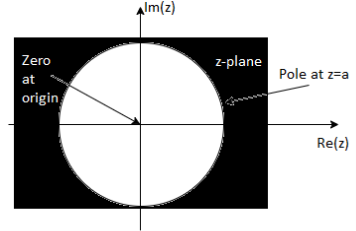
Fig: ROC |z|>|a|
Q11) Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC
A11) X(z) = 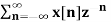
X(z) = 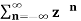 bn u(-n-1) u(-n-1) =0 for n ≥0
bn u(-n-1) u(-n-1) =0 for n ≥0
= 1 for n ≤ -1
= 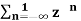 bn =
bn = 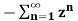 b-1 =
b-1 =
= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1 |z| < |b|
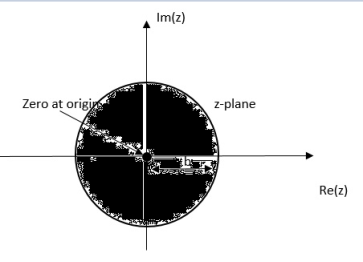
Fig: ROC |z|<|b|
Q12) Find the z-transform of x(n) = an u(n) – bn u(-n-1)
A12) X(z) = 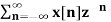
= 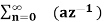 n +
n + 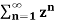 b-1
b-1
= z/z-a + z/z-b ROC |a| < |z| < |b|
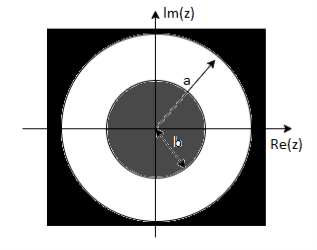
Fig: ROC |a| < |z| < |b|
|b|< |a|
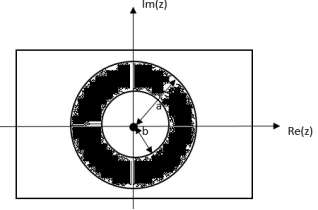
Fig: ROC |b|< |a|
|b| >|a|
Q13) Find the partial fraction method of X(z) = ¼ z-1
(1 – ½ z-1)(1-1/4 z-1)
A13)
X(z) = A + B
Z (1-1/2z-1) (1 – ¼ z-1)
By solving A= 1 and B=-1
Therefore,
X(z) = z - z
z-1/2 z-1/4
x(n) = (1/2) n u(n) – (1/4) n u(n)
Q14) Find the system transfer function H(z) and unit sample response h(n) of the system whose difference equation is below having y(n) as output of system and x(n) as system input?
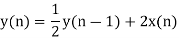
A14)
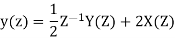
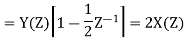
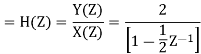
The systems poles lie at Z = ½ and Z=0
H(z)= 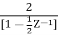
The IZT of above equation gives
H(n) = 2 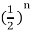 U(n)
U(n)
Q15) Determine Y(z), n≥0 for equation shown below?
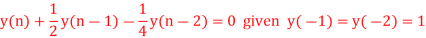
A15) Taking Z-transform of above equation we get
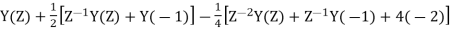 =0
=0
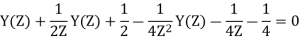
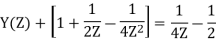
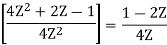
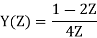
Q16) To find the response of the system s(n+2)−3s(n+1)+2s(n)=δ(n) when all the initial conditions are zero.
A16)
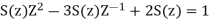
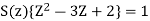
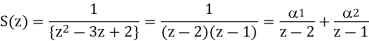
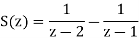
Taking the invese Z-transform of tha above equation, we get
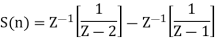
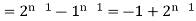
Q17) A DSP system is described by the following differential equation with zero initial condition:

a. Determine the impulse response y(n) due to the impulse sequence x(n) = (n).
b. Determine system response y(n) due to the unit step function excitation, where u(n) = 1 for n 0
A17)
a) By Z transform of above equation we get
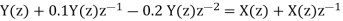
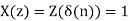
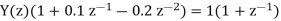
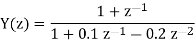
We multiply the numerator and denominator by z2
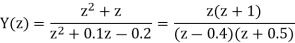
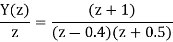
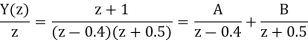
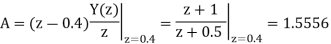
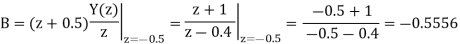
Therefore 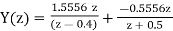
The impulse response of the system will be
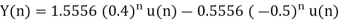
b) The input is step unit function x(n) =u(n)
The z-transform will be
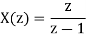
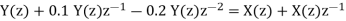
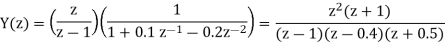
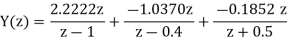
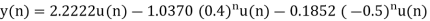
Q18) Solve the difference equation when the initial condition is y (-1) =1
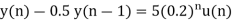
A18) Taking z-transform we get
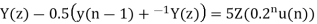
From given initial conditions we have
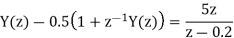
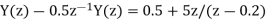
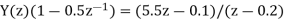
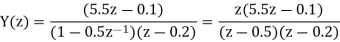
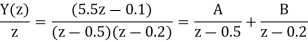
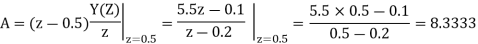
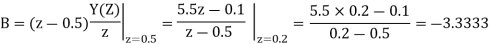
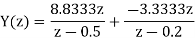
Taking IZT we get
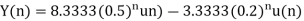
Q19) Find y(n) if
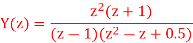
A19) Using partial fraction method we get
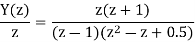
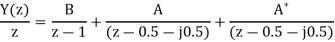
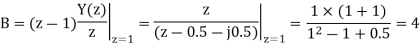
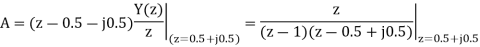
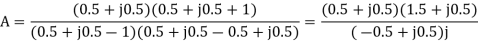
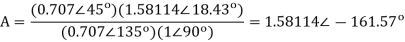
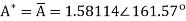
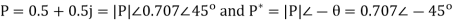
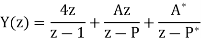
The IZT now is given by following equation
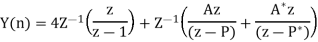

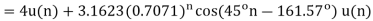
Q20)
(a) Obtain the z-transform of 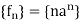
(b) Solve
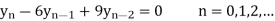

A20)
(a) 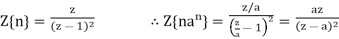 where we have used the property
where we have used the property
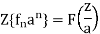
(b) Taking the z-transform of the difference equation and inserting the initial conditions:
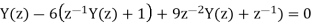
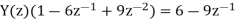
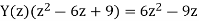
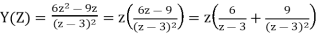 in partial fractions
in partial fractions
From which, using the result (a) on the second term