Unit - 2

Linear Applications of IC Op-Amps

Q1) Design a non-inverting active low pass filter circuit that has a gain of ten at low frequencies, a high-frequency cut-off or corner frequency of 175Hz and an input impedance of 20KΩ.

A1) The voltage gain of the non-inverting amplifier is given as

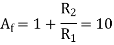
Now assume the value of R1 to be 1KΩ and calculate the value R2 from the above equation.

Hence for a voltage gain of 10, values of R1 and R2 are 1KΩ and 9KΩ respectively. Gain in dB is given as 20LogA = 20Log10 = 20dB

Now we are given with the cut-off frequency value as 175Hz and input impedance value as 20KΩ. By substituting these values in the equation and value of C can be calculated as follows.

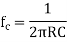
Q2) Assume Rs1 = Rs2 = 15KΩ and capacitor C1 = C2 = 100nF. The gain resistors are R1=1KΩ, R2= 9KΩ, R3 = 6KΩ, and R4 =3KΩ. Design a second-order active low pass filter with these specifications.

A2)

The cut-off frequency is given as

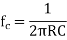
(1)

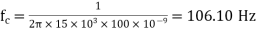
The gain of first stage amplifier is

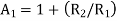
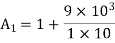
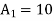
The gain of second stage amplifier is

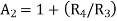
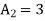
Total Gain of the filter

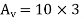
The total gain in dB

(2) 

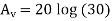
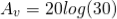
(3) 

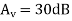
The gain at cut-off frequency is

(4) Gain at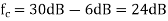

Q3) Consider cut-off frequency value as 10 KHz, pass band gain Amax as 1.5 and capacitor value as 0.02 µF.

A3) The equation of the cut-off frequency is fC = 1 / (2πRC)​

By re-arranging this equation,

We have R = 1 / (2πfC)​

R = 1/ (2π * 10000 * 0.02 * 10-6) = 795.77 Ω​

The pass band gain of the filter is Amax = 1 + (R3/R2) = 1.5

R3 = 0.5 R2​

If we consider the R2 value as 10KΩ, then R3 = 5 kΩ

We can calculate the gain of the filter as follows:

​Voltage Gain for High Pass filter: 

| Vout / Vin | = Amax * (f/fc) /√[1 + (f/fc)²]​

Av(dB) = 20 log10 (Vout/Vin)

Q4) Design a filter with cut-off frequency 4 KHz and the delay rate in the stop band is 40dB/decade. As the delay rate in the stop band is 40dB/decade we can clearly say that the filter is second order filter.

A4) Let us consider the capacitor values as C1= C2 = C = 0.02µF

The equation of the cut-off frequency is fc = 1/ 2πRC Hz

By re-arranging this equation, we have R = 1/ 2πfC

By substituting the values of cut-off frequency as 4 KHz and capacitor as 0.02µF

R = 1.989 KΩ = 2KΩ.

Let the gain of the filter is 1+ R1/R2 = 2

R1 / R2 = 1

R1 = R2

Therefore, we can take R1 = R2 = 10 KΩ

Thus, the obtained filter is shown as below:

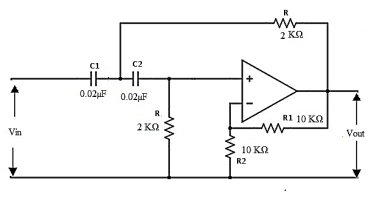
Fig: HPF Designed circuit

Q5) Consider the infinity gain multiple feedback active filter circuit for which the resonating frequency is 1.5 kHz, maximum Voltage gain is 15 and quality factor is 7.

A5) Then component values are calculated as follows:

For Resistors

R1 =Q/ 2πfc CAmax

R2 = Q/ πfc C

And R3 = Q/ 2πfc C(2Q2 - Amax)

Choosing capacitor C1 =C2 =C = 0.02µF

Q= fc / Bandwidth = 0.5 √(R2/ R1) = 7

Applying values to R1, R2, R3 we get R1 = 2.47kΩ, R2 = 74.27 kΩ, R3 = 447.4 kΩ.

We consider that the changed resistor value as R3´ and the changed cut-off frequency value fc´=2 KHz then we can equate for the new resistor value as follows:

R3´ = R3 (fc/fc´)2 = 447.4(1.5/2)2 = 251.66 Ω

Therefore, simply by taking the required frequency we can calculate the new resistor value.

Q6) An active band pass filter that has a voltage gain Av of one (1) and a resonant frequency, ƒr of 1kHz is constructed using an infinite gain multiple feedback filter circuit. Calculate the values of the components required to implement the circuit.

A6) Firstly, we can determine the values of the two resistors, R1 and R2 required for the active filter using the gain of the circuit to find Q as follows.

Av = 1 = -2Q2

QBP = √(1/2) =0.7071

Q = 0.7071 = 0.5 √(R1/R2)

Or R1/R2 =2

Then we can see that a value of Q = 0.7071 gives a relationship of resistor, R2 being twice the value of resistor R1. Then we can choose any suitable value of resistances to give the required ratio of two. Then resistor R1 = 10kΩ and R2 = 20kΩ.

The center or resonant frequency is given as 1kHz. Using the new resistor values obtained, we can determine the value of the capacitors required assuming that C = C1 = C2.

F1 = 1000 Hz =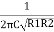 

C = 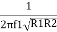= =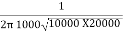11.2nF

The closest standard value is 10nF.

Q7) Find the order of an active low pass Butterworth filter whose specifications are given as: Amax = 0.5dB at a pass band frequency (ωp) of 200 radian/sec (31.8Hz), and Amin = -20dB at a stop band frequency (ωs) of 800 radian/sec. Also design a suitable Butterworth filter circuit to match these requirements.

A7) Firstly, the maximum pass band gain Amax = 0.5dB which is equal to a gain of 1.0593, remember that: 0.5dB = 20*log(A) at a frequency (ωp) of 200 rads/s, so the value of epsilon ε is found by:

1.0593 = =(1 + €2)1/2

€ = 0.3495

Secondly, the minimum stop band gain Amin = -20dB which is equal to a gain of 10 (-20dB = 20*log(A)) at a stop band frequency (ωs) of 800 rads/s or 127.3Hz.

Substituting the values into the general equation for a Butterworth filters frequency response gives us the following:

H(jw) = 1/ √(1+ €2(w/wp)2n)

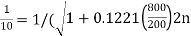
(10)2 = 1 + 0.1221 x 42n

On solving this we get n = 2.42

Since n must always be an integer (whole number) then the next highest value to 2.42 is n = 3, therefore a “a third-order filter is required” and to produce a third-order Butterworth filter, a second-order filter stage cascaded together with a first-order filter stage is required.

From the normalized low pass Butterworth Polynomials table above, the coefficient for a third-order filter is given as (1+s) (1+s+s2) and this gives us a gain of 3-A = 1, or A = 2. As A = 1 + (Rf/R1), choosing a value for both the feedback resistor Rf and resistor R1 gives us values of 1kΩ and 1kΩ respectively as: (1kΩ/1kΩ) + 1 = 2.

Q8) Design a basic wide-band, RC band stop filter with a lower cut-off frequency of 200Hz and a higher cut-off frequency of 800Hz. Find the geometric center frequency, -3dB bandwidth and Q of the circuit.

A8) F = 1/ 2πRC

The upper and lower cut-off frequency points for a band stop filter can be found using the same formula as that for both the low and high pass filters as shown.

Assuming a capacitor, C value for both filter sections of 0.1uF, the values of the two frequency determining resistors, RL and RH are calculated as follows.

Low Pass Filter Section

FL = 1/ 2πRLC = 200Hz and C =0.1 µF

RL = 1/ 2π x 200 x 0.1 10 -6 = 7958Ω or 8kΩ

High Pass Filter Section

FH = 1/ 2πRHC = 800Hz and C =0.1 µF

RH = 1/ 2π x 800 x 0.1 10 -6 = 1990Ω or 2kΩ

From this we can calculate the geometric center frequency, ƒC as:

Fc = √(fL x fH) = √(200x 800) = 400 Hz

fBW = fH - fL = 800 – 200 =600 Hz

Q = Fc/ fBW  = 400/600 = 0.67 OR -3.5 dB

If we make the op-amps feedback resistor and its two input resistors the same values, say 10kΩ, then the inverting summing circuit will provide a mathematically correct sum of the two input signals with zero voltage gain.

Then the final circuit for our band stop (band-reject) filter example will be:

Band Stop Filter Design

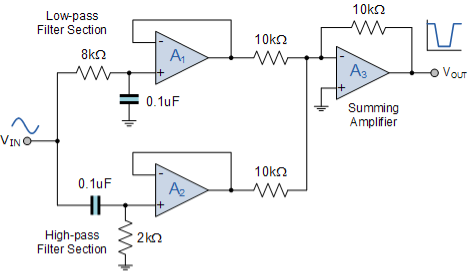
Fig: Band Stop Filter

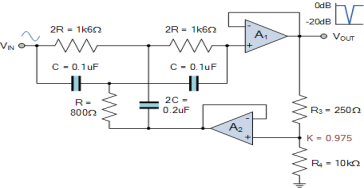
Q9) Design a two op-amp narrow-band, RC notch filter with a center notch frequency, ƒN of 1kHz and a -3dB bandwidth of 100 Hz. Use 0.1uF capacitors in your design and calculate the expected notch depth in decibels.

Data given: ƒN = 1000Hz, BW = 100Hz and C = 0.1uF.

A9) 1. Calculate value of R for the given capacitance of 0.1uF

R = 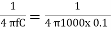x 106

R = 795 Ω

2. Calculate value of Q

Q = FN/ fBW   = 1000/100 =10

3. Calculate value of feedback fraction k

K = 1 – 1/4Q =1- 1/ 4x 10 = 0.975

4. Calculate the values of resistors R3 and R4

K = 0.975 = R4/(R3+R4)

Assuming R4 = 10kΩ then R3 is

R3 = R4 – 0.975 X R4

R3 =250Ω

5. Calculate expected notch depth in decibels, dB

1/Q =1/10 =0.1

fN(dB) = 20 log (0.1) = -20dB

Notch Filter Design

Q10) Design a second-order high-pass Sallen and Key Filter circuit with the following characteristics: ƒC = 200Hz, and Q = 3

A10) To simplify the math’s a little, we will assume that the two series capacitors CA and CB are equal (CA = CB = C) and also the two resistors RA and RB are equal (RA = RB = R).

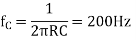
We will choose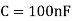

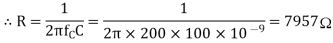
The calculated value of R is 7957Ω, so the nearest preferred value used is 8kΩ.

For Q = 3, the gain is calculated as:

If 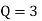then

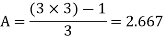
If A = 2.667, then the ratio of R1/R2 = 1.667 as shown.

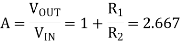
Assume a value of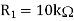

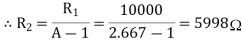
The calculated value of R2 is 5998Ω, so the nearest preferred value used 6000Ω or 6kΩ. This then gives us the final circuit for our Sallen and Key high-pass filter example of

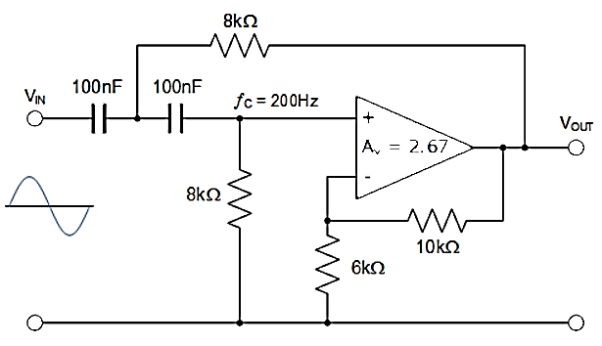
Fig: Sallen and Key High Pass Filter

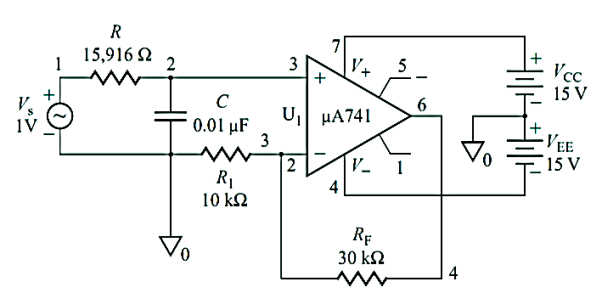
Q11) Design a first-order low-pass filter to give a high cutoff frequency of fo 1 kHz with a pass-band gain of 4. If the desired frequency is changed to fn 1.5 kHz, calculate the new value of Rn?

A11) (a) The high cutoff frequency is fo 1 kHz. Choose a value of C less than or equal to 1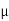 F: let C 0.01 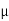F. Using Equation below calculate the value of R

R = 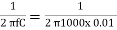x 106 = 15.916 kOhm

Choose values of R1 and RF to meet the pass-band gain K

K= 1+RF ⁄ R1

RF ⁄ R1 = 4-1 =3

If we let R1=10 kOhm, RF= 30kOhm

Calculate the frequency scaling factor, FSF =fo ⁄ fn

FSF = 1kHz/1.5kHz =0.67

Calculate the new value of Rn =FSF x R = 0.67 x 16000= 10.66kOhm

The LPF design is

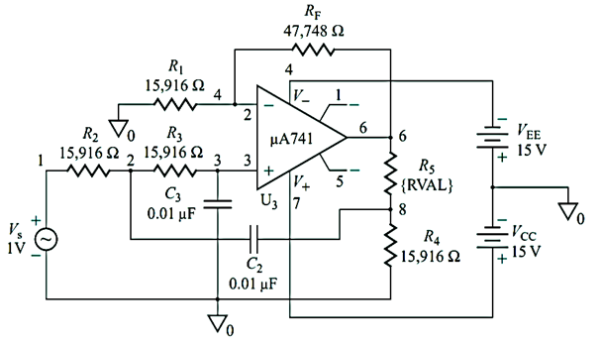
Q12) Design a second-order low-pass filter as in Fig. 12.14, to give a high cutoff frequency of fH =fo =1 kHz, a pass-band gain of K= 4, and Q =0.707, 1, 2, and infinity.

A12) To simplify the design calculations, let R1= R2= R3= R4= R and let C2= C3= C. Choose a value of C less than or equal to 1 F: Let C= 0.01 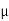F. For R2 =R3 =R and C2 =C3 =C

R= 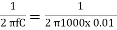x 106 = 15.916 kOhm

Then RF = (K -1)/R1= (4-1) x 15,916= 47,748 Ohm

For Q= 0.707 and K= 4, gives x =1.586 ⁄ K =1.586 ⁄ 4= 0.396.

R5/R4=1-x/x

Which, for x= 0.396 and R4= R= 15,916 Ohm

R5= 1.525 x 15,916= 24,275 Ohm

For Q= 1 and K= 4, gives 3-xK= 1 or x= 2 ⁄ K= 0.5

R5= R= 15,916 Ohm

For Q= 2 and K= 4, gives 3-xK= 1/2 or x= 2.5 ⁄ K= 0.625 Ohm

R5 = 0.6R = 9550 Ohm

For Q= infinity and K= 4, gives 3-xK= 1/Q=0 or x= 3 ⁄ K= 0.75 Ohm

R5 = 0.333R = 5305 Ohm

The design of LPF with above circuit parameters is shown below. This is a PSpice model

Q13) Designing a second-order low-pass Butterworth filter for |H(jωo)|= 1. Design a second-order Butterworth low-pass filter as in Figure below to yield H(jωo)= 1 (or 0 dB), a cutoff frequency of fo= 1 kHz, and Q= 0.707.

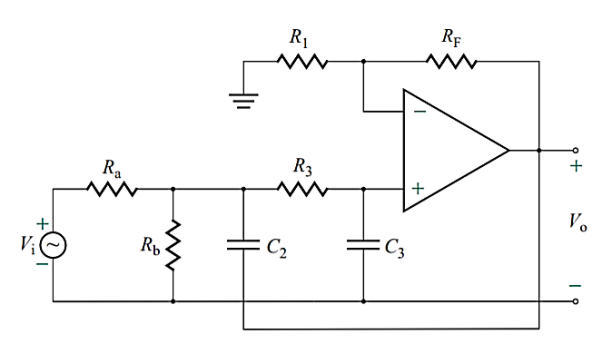
A13)

For the Butterworth response, Q= 0.707. From above example we have C= 0.01 F and R= 15,916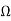

K = 3 – (1/ Q) = 3 – (1/ 0.707) = 1.586

RF = (K - 1)/R1 = (1.586 - 1) * 15,916 = 9327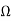

Ra = RK /3 - K = [15,916 * 1.586]/ [3 - 1.586] = 17,852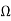

Rb = RK /2K - 3 = [15,916 * 1.586]/ [(2 * 1.586) – 3] = 146,760

|H(j0)|= 3 - K = 3 - 1.586 = 1.414

The design is shown below

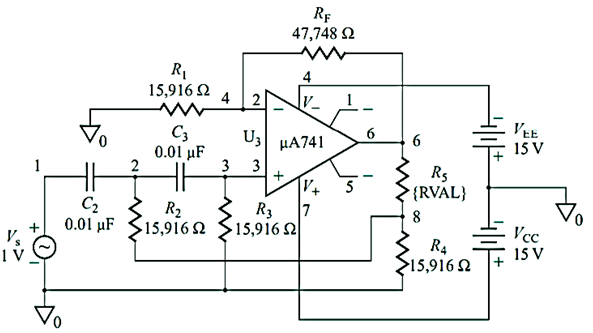
Q14) Design a second-order high-pass filter as in Figure below, with a cut-off frequency of fo= 1 kHz, a pass-band gain of K 4, and Q 0.707, 1, 2, and infinity.

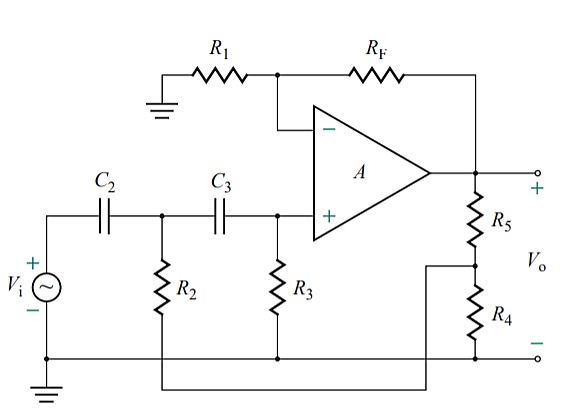
A14) Since high-pass filters are formed simply by interchanging the Rs and Cs of the input RC network and since fo= 1 kHz, we can use the values of R and C that were determined for the second-order low-pass filter of Example above—that is, C= 0.01 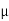F, and R4= R= 15,916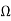

For Q= 0.707, R5= 24,275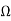

For Q= 1, R5= R= 15,916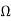

For Q 2, R5= 0.6R= 9550

For Q=infinity, R5= 0.3333R= 5305

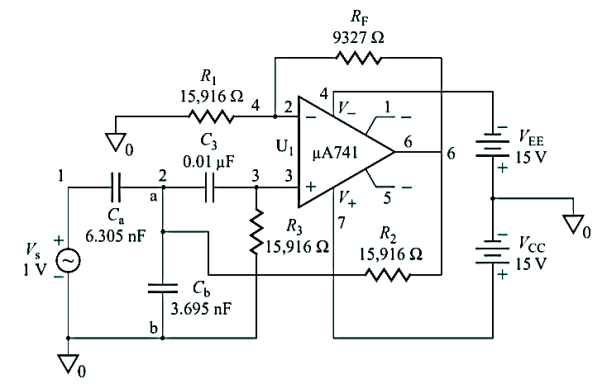
Q15) Design a second-order Butterworth high-pass filter as in Figure below to yield |H(j∞)|= 1 (or 0 dB), a cut-off frequency of fo= 1 kHz, and Q= 0.707.

A15) For Q= 0.707, and from above question we take C= 0.01 F, and R= 15,916

K = 3 – 1/ Q = 3 – 1/ 0.707 = 1.586

RF= (K - 1)/R1= (1.586 - 1) x 15,916= 9327

Ca = C/ K = 0.01 F/ 1.586 = 6.305 nF

Cb = C(K - 1)/ K = 0.01 F * (1.586 - 1) /1.586 = 3.695 nF

Second-order high-pass Butterworth filter for PSpice simulation is below

Q16) Designing a wide-band-pass filter (a) Design a wide-band-pass filter with fL= 10 kHz, fH= 1 MHz, and a pass-band gain of KPB= 16. (b) Calculate the value of Q for the filter.

A16)

a) Let the gain of the high-pass section be KH= 4. For the first-order high-pass section, fL= 10 kHz

We let C= 1 nF

R= 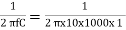x 109 = 15.915 k

KH= 1+RF/R1

4= 1+ RF/R1

RF/R1=3

If we let R1= 10 k 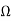, RF= 3R1= 30 k 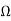. For the first-order low-pass section, fH= 1 MHz and the desired gain is KL= KPB ⁄ KH =16 ⁄ 4 =4

We let C′= 10 pF

R’= 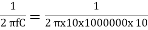x 1012=15.915 k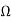

KL= 1+R’F/R’1

4= 1+ R’F/R’1

R’F/R’1=3

b) fC = √10 kHz * 1 MHz = 100 kHz

BW 1 MHz - 10 kHz= 990 kHz

Q = (100kHz)/1MHz-10kHz) = 0.101

The circuit for First-Order BPF is shown below.

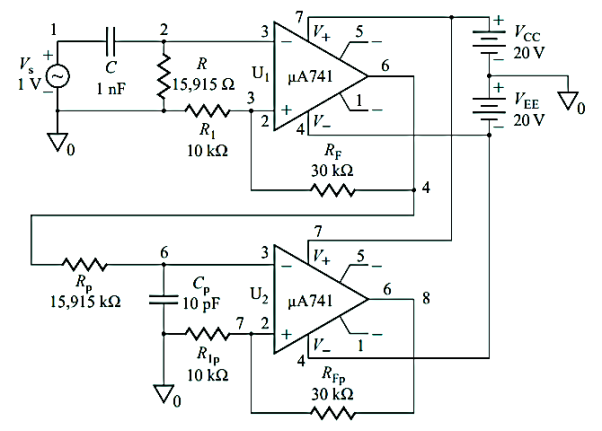
Q17) Explain about KHN filters?

A17) The Sallen-Key and Multiple Feedback filters have the advantage that they use a small number of components, especially op-amps. They were particularly popular when op-amps were relatively expensive. However, it may be impossible to design a circuit with a particular transfer function or the resulting design may be sensitive to variations in component values. In these situations, the best approach may be to take advantage of reductions in component costs, which mean that op-amps are now commonly available with up to four op-amps in a single package and use a filter design which contains several op-amps.

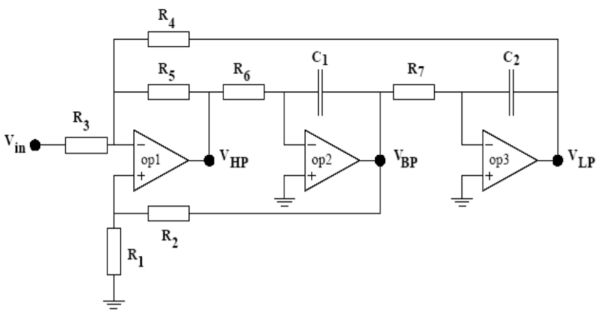
Figure: An inverting state-variable or KHN filter

One type of filter that contains several op-amps in a single stage is the state variable or KHN filter, first proposed by Kerwin, Huelsman and Newcomb. As shown in Figure above this filter contains three op-amps from which highpass, band-pass and low-pass responses are available simultaneously.

The first step in analysing the circuit is to break it down into the different functional blocks. The op-amp labelled op1 has quite a complicated looking set of connections. However, the connections to the other two op-amps are much simpler, for example isolating the part of the circuit containing op3 leads to the simple circuit shown in Figure

Figure: The connections in op-amp op3 in the KHN Filter in Figure above

This is simply the circuit with a capacitor acting as the input impedance and a resistor in the feedback loop. The relationship between the input and the output of this circuit is therefore

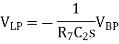
In fact, op2 has equivalent connections, and so the relationship between the output of this circuit block and its input is

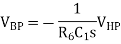
Now consider the remaining op-amp in the circuit, op1. The components connected to op1 mean that the voltage at the output of this op-amp depends upon a linear combination of the input to the filter circuit and the outputs from the two other op-amps within the filter. This op-amp therefore has three inputs and linear superposition can be used to derive an expression for its output. In linear superposition the total output is found by considering the response of the circuit to each voltage or current source separately. Any voltage source that is not being considered acts as a short-circuit and any current source that is not being considered acts as an open-circuit. For the three inputs to the circuit around op1, short-circuiting the output from op2 shows that for Vin and VLP op1 is configured as a summing amplifier that adds the two components.

To determine the contribution to the output of op1 from the output from op2 by superposition, short-circuit both Vin and VLP. This means that both R3 and R4 and connect the inverting op-amp input to ground, these two resistors therefore act in parallel so that the voltage at the inverting op-amp input is

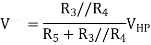
Similarly, the voltage at the non-inverting input is

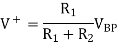
For the ideal op-amp V- = V+

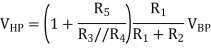
This contribution can then be combined with the other two contributions to give

Then remember that the analysis of the responses of the other two op-amps gave

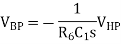
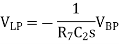
These two expressions can then be included into

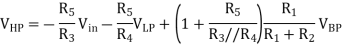
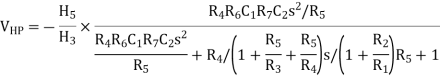
This is the transfer function of a second-order high-pass filter, with

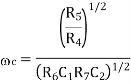
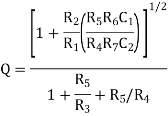
The band-pass filter response can then be obtained from the high-pass response using

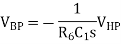
In turn the expression for the band-pass response of the system can be used to obtain an expression for the low-pass filter response using

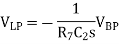
Q18) Explain simulation of inductor?

A18) Before the introduction of the transistor and the integrated circuit, coils of wire with large inductance were used in electronic filters. An inductor can be replaced by a much smaller assembly consisting of a capacitor, operational amplifiers or transistors, and resistors. This is especially useful in integrated circuit technology where building inductors from large loops of wire is impractical.

The circuit in Figure below reverses the operation of a capacitor, thus making a simulated inductor. An inductor resists any change in its current, so when a dc voltage is applied to an inductance, the current rises slowly, and the voltage falls as the external resistance becomes more significant.

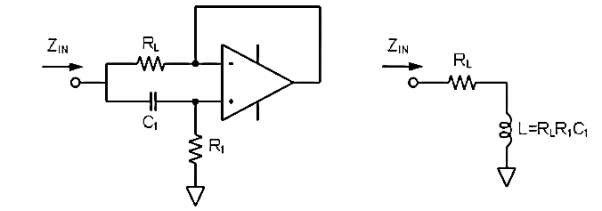
Fig: Simulated Inductor

An inductor passes low frequencies more readily than high frequencies, the opposite of a capacitor. An ideal inductor has zero resistance. It passes dc without limitation, but it has infinite impedance at infinite frequency.

For the circuit in figure above, if a DC voltage step is suddenly applied to the inverting input through resistor RL, the op amp ignores the sudden step because the change is also coupled directly to the non-inverting input via C1. The op amp represents high impedance, just as an inductor does. As C1 charges through R1, the voltage across R1falls, so the op-amp draws current from the input through RL. This continues as the capacitor charges, and eventually the op-amp has an input and output close to virtual ground because the lower end of R1 is connected to ground.

When C1 is fully charged, resistor RL limits the current flow, and this appears as a series resistance within the simulated inductor. This series resistance limits the Q of the inductor. Real inductors generally have much less resistance than the simulated variety.

There are some limitations of a simulated inductor like this:

• One end of the inductor is connected to virtual ground.
• The simulated inductor cannot be made with high Q, due to the series resistor RL.
• It does not have the same energy storage as a real inductor. The collapse of the magnetic field in a real inductor causes large voltage spikes of opposite polarity. The simulated inductor is limited to the voltage swing of the op amp, so the flyback pulse is limited to the voltage swing.

Q19) Write difference between Active and Passive Filters?

A19)