Unit - 4

Computational Learning Theory

Q1) Differentiate between Parametric Machine Learning Algorithms Nonparametric Machine Learning Algorithms

A1)

Q2) Differentiate b/w Lazy Learning vs Eager Learning

A2)

Q3) What is K-NN in Classification?

A3)

K-nearest-neighbor classification was developed from the need to perform discriminant analysis when reliable parametric estimates of probability densities are unknown or are difficult to determine. When K-NN is used for classification, the output is easily calculated by the class having the highest frequency from the K-most similar instances. The class with a maximum vote is taken into consideration for prediction.

The probabilities of Classes can be calculated as the normalized frequency of samples that belong to each class in the set of K most similar instances for a new data instance.

For example, in a binary classification problem (class is 0 or 1):

p(class=0) = count(class=0) / (count(class=0)+count(class=1))

If you are using K and you have an even number of classes (e.g. 2) it is a good idea to choose a K value with an odd number to avoid a tie. And the inverse, use an even number for K when you have an odd number of classes.

Ties can be broken consistently by expanding K by 1 and looking at the class of the next most similar instance in the training dataset.

Q4) What is “Error” in Machine Learning? 

A4)

Error in Machine Learning is the difference in the expected output and the predicted output of the model. It is a measure of how well the model performs over a given set of data.

There are several methods to calculate error in Machine Learning. One of the most commonly used terminologies to represent the error is called the Loss/Cost Function. It is also known as the Mean Squared Error (or MSE) and is given by the following equation:

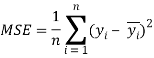
n = Number of data-points over which the error is calculated

y = The expected output of the model

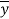= The predicted output of the model

The necessity of minimization of Errors: As it is obvious from the previously shown graphs, the higher the error, the worse the model performs. Hence, the error of the prediction of a model can be considered as a performance measure: The lower the error of a model, the better it performs. 

In addition to that, a model judges its own performance and trains itself based on the error created between its own output and the expected output. The primary target of the model is to minimize the error to get the best parameters that would fit the data perfectly. 

Q5) What is Bias?

A5)

Bias is used to allowing the Machine Learning Model to learn in a simplified manner. Ideally, the simplest model that can learn the entire dataset and predict correctly on it is the best model. Hence, bias is introduced into the model in the view of achieving the simplest model possible.

Parameter based learning algorithms usually have high bias and hence are faster to train and easier to understand. However, too much bias causes the model to be oversimplified and hence underfits the data. Hence these models are less flexible and often fail when they are applied to complex problems.

Mathematically, it is the difference between the model’s average prediction and the expected value.

Q6) What is a Variance?

A6) Variance in data is the variability of the model in a case where different Training Data is used. This would significantly change the estimation of the target function. Statistically, for a given random variable, Variance is the expectation of squared deviation from its mean. 

In other words, the higher the variance of the model, the more complex the model is and it can learn more complex functions. However, if the model is too complex for the given dataset, where a simpler solution is possible, a model with high Variance causes the model to overfit. 

When the model performs well on the Training Set and fails to perform on the Testing Set, the model is said to have Variance.

Q7) What are the Characteristics of a biased model 

A7)

A biased model will have the following characteristics:

• Underfitting: A model with high bias is simpler than it should be and hence tends to underfit the data. In other words, the model fails to learn and acquire the intricate patterns of the dataset. 
• Low Training Accuracy: A biased model will not fit the Training Dataset properly and hence will have low training accuracy (or high training loss). 
• Inability to solve complex problems: A Biased model is too simple and hence is often incapable of learning complex features and solving relatively complex problems.

Q8) What are some characteristics of a model with Variance? 

A8)

A model with high Variance will have the following characteristics:

• Overfitting: A model with high Variance will tend to be overly complex. This causes the overfitting of the model.
• Low Testing Accuracy: A model with high Variance will have very high training accuracy (or very low training loss), but it will have a low testing accuracy (or a low testing loss). 
• Overcomplicating simpler problems: A model with high variance tends to be overly complex and ends up fitting a much more complex curve to relatively simpler data. The model is thus capable of solving complex problems but incapable of solving simple problems efficiently.

Q9) Differentiate between Gradient Descent & Simple Linear Regression

A9)

Gradient Descent

Gradient Descent is an optimization algorithm that helps machine learning models to find out paths to a minimum value using repeated steps. Gradient descent is used to minimize a function so that it gives the lowest output of that function. This function is called the Loss Function. The loss function shows us how much error is produced by the machine learning model compared to actual results. Our aim should be to lower the cost function as much as possible. One way of achieving a low-cost function is by the process of gradient descent. The complexity of some equations makes it difficult to use, a partial derivative of the cost function with respect to the considered parameter can provide optimal coefficient value. You may refer to the article on Gradient Descent for Machine Learning.

Simple Linear Regression

Optimization is a big part of machine learning and almost every machine learning algorithm has an optimization technique at its core for increased efficiency. Gradient Descent is such an optimization algorithm used to find values of coefficients of a function that minimizes the cost function. Gradient Descent is best applied when the solution cannot be obtained by analytical methods (linear algebra) and must be obtained by an optimization technique.

Q10) Explain the Working of the KNN Algorithm.

A10)

K-nearest neighbours (KNN) algorithm uses ‘feature similarity’ to predict the values of new datapoints which further means that the new data point will be assigned a value based on how closely it matches the points in the training set. We can understand its working with the help of the following steps −

Step 1 − For implementing any algorithm, we need a dataset. So during the first step of KNN, we must load the training as well as test data.

Step 2 − Next, we need to choose the value of K i.e. the nearest data points. K can be any integer.

Step 3 − For each point in the test data do the following −

• 1 − Calculate the distance between test data and each row of training data with the help of any of the methods namely: Euclidean, Manhattan, or Hamming distance. The most commonly used method to calculate distance is Euclidean.
• 2 − Now, based on the distance value, sort them in ascending order.
• 3 − Next, it will choose the top K rows from the sorted array.
• 4 − Now, it will assign a class to the test point based on the most frequent class of these rows.

Step 4 − End