Unit 1
Elements of Satellite Communication
Q1) Explain the components of the satellite?
A1) Satellites are used to transfer information from one place to another using communication satellites in Earth's orbit. Satellite communication began in 1957 and the first artificial satellite launched was Sputnik I by the USSR. Satellite communication can be one way as well. In this case, the transmission of a signal from the transmitter of the first earth satellite and the receiver of the second earth satellite is in one direction.
In two-way communication, the information is exchanged between the two earth stations. There are two uplinks and two downlinks required to achieve two ways communication.
The main elements of communication satellite are
i) Uplink
Ii) Transponders
Iii) Downlink
The block diagram of satellite communication is shown below. A communication satellite is an R.F repeater.
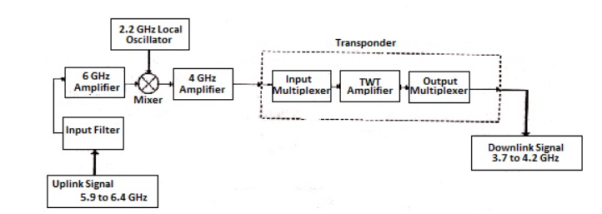
Fig: Block Diagram of Satellite Communication
The uplink frequencies used are of range 5.9GHz-6.4GHz these frequencies are converted to lower frequencies and amplified. The mixers and local oscillators are used to convert the higher frequency uplink signals to lower frequency signals. The com satellite receives this signal amplifies it and then transmits it so that there is no interference in the uplink and downlink signals.
The transponders provide the medium for two-way communication. The downlink frequency used for transmission is from the range of 3.7GHz to 4.2GHz. The number of transponders per satellite depends upon the task which the satellite needs to do. For television broadcast, two transponders are used in a satellite.
Q2) List the advantages and applications of satellite communication?
A2)
Advantages
The advantages of satellite communication are
- They are easy to install.
- Communication can be set up in every part of the earth with the help of satellites.
- The network is controlled by the user.
- The elasticity of these circuits is excellent
Applications
The applications of satellite communication are
- Telephone
- Television
- Digital cinema
- Radio broadcasting
- Amateur radio
- Internet access
- Military
Q3) Derive the equation for a time period of the satellite?
A3) The satellite which revolves around the earth experiences a force from the earth which tries to pull the satellite. This force is called a centripetal force. The equation for such force is given as
FI = m x 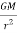
The centrifugal force which tries to pull the satellite away from earth is due to the sun and moon and is given as
Fo = m x 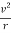
When the force on the satellite is balanced then
m x 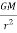 = m x
= m x 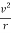
v= 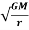 (1)
(1)
Where
M= mass of earth 5.98 x 1024 kg
G = gravitational constant 6.672 x 10-11 N-m2/kg2
r = Distance from satellite to centre of the earth
m= mass of the satellite
The centrifugal acceleration is given by a=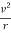
Since distance divided by velocity equals time to travel that distance the period of the satellite orbit T is given by
T = 2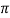 r/v
r/v
T= 2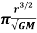 (2)
(2)
Q4) Derive the equation of orbit of the satellite?
A4)
The equation for gravitational force on the satellite is given as
F = - 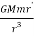 (3)
(3)
r’ is the vector locating moving satellite w.r.t the centre of the earth.
The above equation can also be written as
F = m 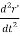 (4)
(4)
From 3 and 4 we get
-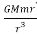 = m
= m 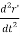
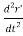 +
+ 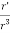 GM = 0
GM = 0
The solution of the above equation gives six constants called orbital elements. The solution for the above equation is difficult to obtain so new coordinates can be assumed or considered.
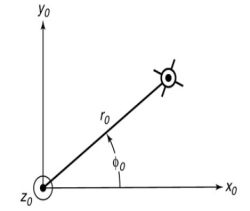
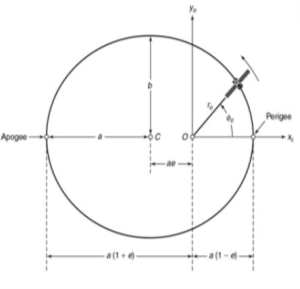
Fig: Polar Coordinates for satellites orbit
x0 = r0 cosφ0
y0 = r0 sinφ0
Now we can write the differential equation as
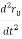 - r0 (
- r0 (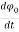 ) = -
) = -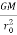
The solution for above equation is given below which is the equation for orbit of satellite
r0 = 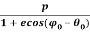
p = h2/GM
Where
e= eccentricity
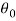 = constant
= constant
h = magnitude of orbital angular momentum of the satellite.
Q5) State Kepler’s law of planetary motion?
A5) The Kepler’s Law of Planetary Motion are
i) The orbit of any smaller body about a larger body is always an ellipse with the centre of mass of the larger body as one of the two foci.
Ii) The orbit of the smaller body sweeps out equal areas in equal time.
Iii) The square of the period of revolution of the smaller body about the larger body equals the constant multiplied by the third power of the semi-major axis of the orbital ellipse T2= 4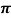 2a3/GM
2a3/GM
Q6) Define apogee and perigee?
A6) The length of the semimajor axis is given by
a= p/(1-e2)
The length of the semi-minor axis is given by
b= a(1-e2)1/2
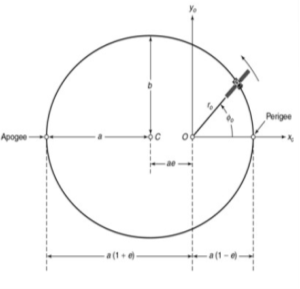
The point in the orbit where the satellite is closest to the earth is called perigee and the point where the satellite is farthest from the earth is called apogee. The apogee and perigee are the exact opposite of each other. The orbital period T will be
T2= 4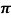 2a3/GM
2a3/GM
Q7) What are geosynchronous and geostationary satellites?
A7) The satellite which has an orbital period same as the rotation of the earth they are called a geosynchronous satellite. These satellites stay in the same area every day for a particular time. The orbit of such satellites is called geosynchronous orbits.
The geostationary satellite which is at 00 to the equatorial plane is a geostationary satellite. They are placed 35000 km above the equator and have an orbital period equal to a sidereal day.
The geosynchronous satellites are used in broadcasting TV cables, internet, voice, and data communication.
The geostationary satellites are used for a weather forecast. INSAT from India is a geostationary satellite.
Q8) List the orbital effects in the communication system of the satellite?
A8) The orbital effects in the communication system performance are listed below.
i) When the observer is stationary then the frequency of the moving transmitter varies with the transmitter’s velocity relative to the observer. The relation between the transmitted and received frequency is given as
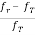 =
= 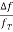 =
= 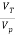
fT: transmitted frequency
fr: received frequency
If the transmitter is moving away from the receiver then the change in frequency is called Doppler Shift.
i) There is a cyclic variation in the position of the satellite w.r.t earth daily. Due to this variation, there is a change in the range between the satellite and the user terminals. The TDMA technique if used should be paid attention to the timing of the frames. The LEO satellite can have path loss due to range variations.
Ii) The solar eclipse phenomenon affects satellite performance. The satellite will not receive any power during the eclipse. To avoid this the batteries are designed such that they do not discharge quickly. The batteries are normally discharged to the maximum and fully charged before the eclipse.
Iii) There is one more phenomenon of the equinox. During this period the sun becomes a hot source. The earth station receives the signal from the satellite and also some noise temperature. This can be handled by the user with his choice.
Q9) Explain the complete launch process of the satellite?
A9) The launch of a satellite is a very crucial phase as our main aim is to place the satellite in the defined orbit. The satellites are designed to be compatible with more launch vehicles. There are four stages for launching a satellite.
i) The first stage of the launch vehicle contains rockets and fuel for lifting the satellite along with the launch vehicle from the ground.
Ii) The second stage of the launch vehicle contains smaller rockets. These are ignited after the completion of the first stage. They have their fuel tanks to send the satellite into space.
Iii) The third (upper) stage of the launch vehicle is connected to the satellite fairing. This fairing is a metal shield, which contains the satellite and it protects the satellite.
Iv) The satellite gets separated from the upper stage of the launch vehicle when it has been reached out of Earth's atmosphere. Then, the satellite will go to a transfer orbit. This orbit sends the satellite higher into space.
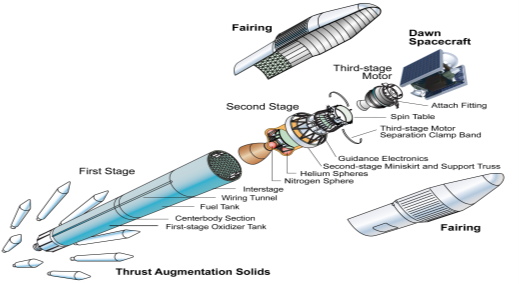
Fig: Satellite Launch system
Q10) What is elevation angle. Derive its expression?
A10) It is the angle between the vertical plane and line pointing to the satellite.
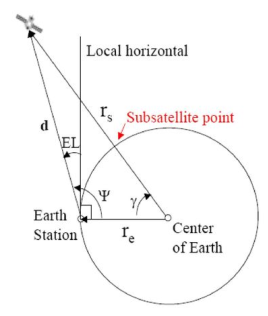
Fig: The calculation of elevation angle
Then
Cos (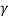 ) = cos (Le) cos (Ls) cos (ls-le) + sin (Le) sin (Ls)
) = cos (Le) cos (Ls) cos (ls-le) + sin (Le) sin (Ls)
The magnitude of vector joining the earth, satellite, and earth station is given as
d = rs [1+( 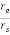 )2 – 2(
)2 – 2(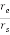 ) cos
) cos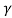 ]1/2
]1/2
The elevation angle is related to the central angle by
El = 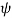 - 900
- 900
The equation for elevation angle will be
Cos (El) = 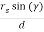 =
= 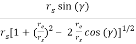
Where:
re = vector from centre of the earth to the earth station
d = vector from an earth station to satellite.
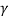 = central angle
= central angle
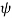 = angle between re to d
= angle between re to d
Ls = substation point at north latitude
Le = west longitude