Unit 1
Introduction to Vector Algebra
Q1) Explain the rectangular co-ordinate system?
A1) A point in rectangular co-ordinate system is located by three co-ordinates namely x,y and z co-ordinates. The point can be reached by moving from origin the distance of x in x-direction , distance of y in y-direction and finally distance of z in z direction.
Consider a point P having co-ordinates x1,y1 and z1 which can be positive or negative.
The point Q(3,-1,2) can be shown as
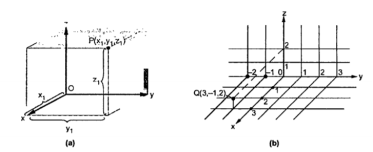
Figure . Rectangular co-ordinate system
Base vector :
The base vector are the unit vectors that are oriented along the directions of the co-ordinate axes of the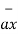 given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore
given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore 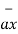 ,
,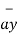 and
and 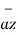 are the base vectors of the cartesian co-ordinate system.
are the base vectors of the cartesian co-ordinate system.
Any point of the x-axis having (x1,0,0) can be represented by a vector joining origin to this point to this point and denoted as x1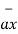 .
.
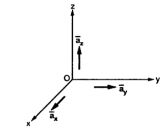
Figure . Base vector
Position and Distance vectors :
Consider a point P(x1,y1,z1) in cartesian co-ordinate system as shown in figure. Then the position vector of point P from the origin directed from origin to point P. This is called radius vector as shown in figure.
The three components of position vector oriented along the three co-ordinate axes with magnitudes x1,y1and z1. Thus the position vector of point P can be represented as
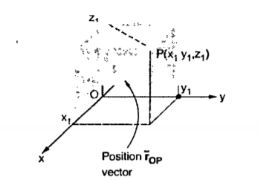
Figure . Position vector
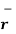 OP= x1
OP= x1 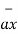 + y1
+ y1 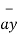 + z1
+ z1 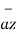
The magnitude of this vector in terms of three mutually perpendicular components is given by
|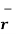 OP|=
OP|=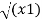 2 + (y1) 2+ (z1) 2
2 + (y1) 2+ (z1) 2
Thus, if point P has co-ordinates (1,2,3) then its position vector is
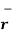 OP=1
OP=1 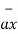 + 2
+ 2 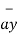 + 3
+ 3 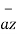
And
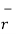 OP =
OP =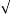 (1) 2 + (2) 2 + (3) 2 =
(1) 2 + (2) 2 + (3) 2 = 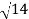 = 3.7416
= 3.7416
Consider two points in a cartesian coordinate system P and Q with the co-ordinates (x1,y1,z1) and (x2,y2,z2) respectively. The individual position vectors of the points are
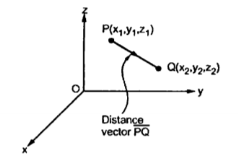
Figure. Cartesian coordinate system
 = x1
= x1  + y1
+ y1 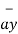 + z1
+ z1 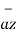
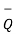 = x2
= x2 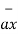 + y2
+ y2 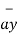 + z2
+ z2 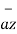
Then the displacement from P to Q is represented by the distance vector 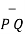 and is given by
and is given by
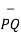 =
= 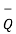 -
- 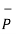 = [x2 -x1]
= [x2 -x1] 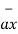 + [ y2 -y1]
+ [ y2 -y1] 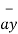 + [z2 -z1]
+ [z2 -z1] 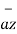
This is called separation vector.
The magnitude of the vector is given by
|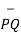 | = √ (x2 -x1) 2 + (y2 -y1) 2 +(z2 – z1) 2
| = √ (x2 -x1) 2 + (y2 -y1) 2 +(z2 – z1) 2
This is called as distance formula.
The unit vector along the direction PQ is given by
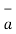 PQ= Unit vector along PQ =
PQ= Unit vector along PQ = 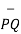 / |PQ|
/ |PQ|
Q2) Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
The vector from A to C
The unit vector from B to A
The distance from B to C
The vector from A to the mid-point of the straight line joining B to C.
A2) The position vectors for the given points are :
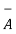 = 3
= 3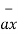 - 2
- 2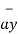 +
+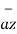 .
.
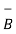 = -3
= -3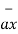 - 3
- 3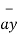 +5
+5 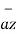 .
.
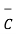 = 2
= 2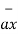 +6
+6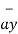 -4
-4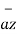 .
.
i) The vector from A to C is
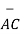 =
= 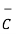 -
- 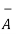 = [ 2-3]
= [ 2-3] 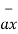 +[6–(-2)]
+[6–(-2)]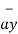 +[-4-1]
+[-4-1] 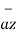 .
.
= - 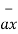 + 8
+ 8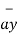 -5
-5 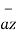 .
.
Ii) For unit vector from B to A obtain the distance vector 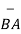 first
first
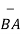 =
= 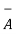 -
- 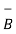
= [ 3 – (-3)]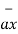 + [ (-2) –(-3) ]
+ [ (-2) –(-3) ] 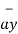 + [ -4-1]
+ [ -4-1] 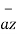
= 6 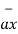 +
+ 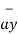 -4
-4 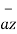 .
.
|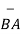 | =
| = 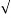 (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
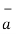 BA =
BA = 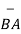 / |
/ |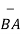 | = 6
| = 6 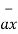 +
+ 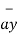 -4
-4 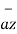 ./ 7.2801
./ 7.2801
Iii) For distance between B and C
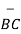 =
= 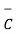 -
- 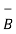 = [ 2 –(-3 ]
= [ 2 –(-3 ] 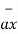 + [6-(-3)]
+ [6-(-3)] 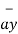 +[-4) –(-5)]
+[-4) –(-5)] 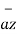 = 5
= 5 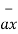 + 9
+ 9 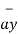 – 9
– 9 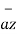
Distance BC = 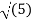 2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
Iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
Q3) Explain the transformation from Rectangular to cylindrical
A3) The transformation of rectangular to cylindrical coordinates requires that we find the components of the rectangular coordinate vector A in the direction of the cylindrical coordinate unit vectors using dot product.
Transformation:
(Ax,Ay,Az) ----- (Ar,Aɸ,Az)
The required dot products are
Ar = A. 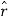 = Ax .
= Ax .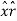 + Ay
+ Ay 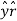 + A.
+ A. 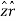 = Ax .
= Ax .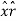 + Ay
+ Ay 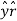
Aɸ = A. 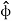 = Ax .
= Ax .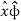 + Ay
+ Ay 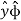 + A.
+ A. 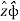 = Ax .
= Ax .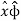 + Ay
+ Ay 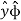
Az = A. 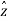 = Ax .
= Ax .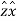 + Ay
+ Ay 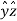 + Az.
+ Az. 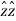 = Az
= Az
Where 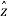 .
. 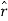 =0
=0 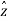 .
. 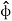 =0
=0 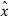 .
. 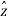 =0
=0 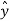 .
. 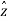 =0
=0 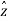 .
. 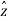 =1
=1
The four remaining unit vector dot products are determined according to the geometry relationships between the two coordinate systems.
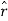 = cos ɸ
= cos ɸ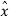 + sin ɸ
+ sin ɸ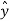
ɸ = - sin ɸ 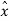 + cos ɸ
+ cos ɸ 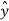
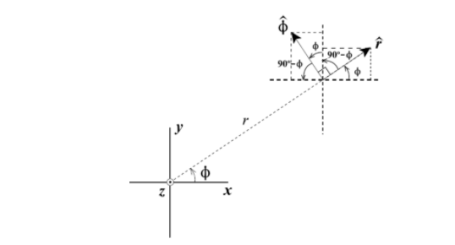
Figure. Rectangular co-ordinate
 .
.  =
=  . ( cos ɸ
. ( cos ɸ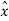 + sin ɸ
+ sin ɸ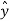 ) = cos ɸ
) = cos ɸ
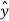 .
. 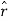 =
= 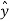 . ( cos ɸ
. ( cos ɸ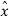 + sin ɸ
+ sin ɸ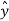 ) = sin ɸ
) = sin ɸ
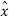 . ɸ =
. ɸ = 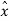 . ( -sin ɸ
. ( -sin ɸ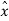 + cos ɸ
+ cos ɸ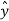 ) = -sin ɸ
) = -sin ɸ
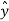 . ɸ =
. ɸ = 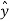 . ( -sin ɸ
. ( -sin ɸ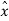 + cos ɸ
+ cos ɸ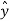 ) = cos ɸ
) = cos ɸ
The resulting cylindrical coordinate vector is A = Ar . 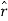 + A ɸɸ + Az
+ A ɸɸ + Az 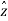
= (Ax cos ɸ + Ay sin ɸ) 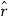 + (Ay cos ɸ - Ax sin ɸ) ɸ + Az
+ (Ay cos ɸ - Ax sin ɸ) ɸ + Az 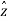
The rectangular to cylindrical transformation is
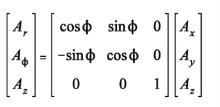
Q4) Write a short on line integral?
A4) The line integrals of vector fields as a line integral with respect to arc length as follows,
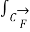 . d
. d 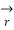 =
= 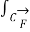 .
. 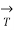 ds
ds
Where →T(t) is the unit tangent vector and is given by,
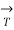 (t) =
(t) = 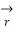 ’(t) ||
’(t) ||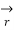 ’(t)||
’(t)||
To compute line integrals with respect to arc length we can see that this second form is equivalent to the first form given above.
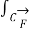 . d
. d 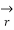 =
= 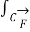 .
. 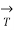 ds
ds
= 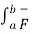 (
( 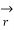 ‘(t) / ||
‘(t) / || 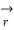 ‘(t) || ||
‘(t) || ||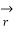 ‘(t) || dt
‘(t) || dt
= 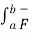 (
( 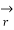 ‘(t) ) .
‘(t) ) . 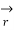 ‘(t) dt
‘(t) dt
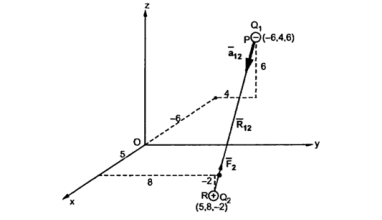
Q5) A charge Q1=-20µC is located at P(-6,4,6) and a charge Q2=50µC is located at R(5,8,-2) in a free space . Find the force exerted on Q2 by Q1 in vector form. The distances given are in meters.
A5) From the co-ordinates of P and R the respective position vectors are :
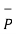 = -6
= -6 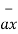 + 4
+ 4 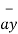 + 6
+ 6 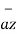
And
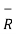 = 5
= 5 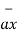 + 8
+ 8 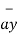 -2
-2 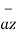
The force on Q2 is given by
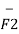 = Q1 Q2 / 4 π
= Q1 Q2 / 4 π 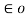 R212 .
R212 .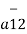
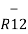 =
=  =
= 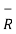 -
- 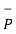 = [ 5 –(-6)]
= [ 5 –(-6)] 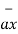 + (8-4)
+ (8-4) 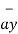 + [-2-(-6)
+ [-2-(-6) 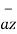 ]
]
= 11 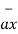 + 4
+ 4 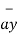 - 8
- 8 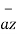
|R12| = 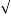 (11) 2 + (4) 2 +(-8) 2 = 14.1774
(11) 2 + (4) 2 +(-8) 2 = 14.1774
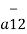 =
= 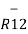 / |
/ |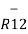 | = 11
| = 11 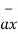 + 4
+ 4 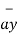 -8
-8 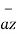 / 14.1774
/ 14.1774
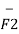 = -20 x 10 -6 x 50 x 10 -6 / 4 π x 8.854 x 10 -12 x (14.1774) 2 [
= -20 x 10 -6 x 50 x 10 -6 / 4 π x 8.854 x 10 -12 x (14.1774) 2 [ 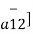
= -0.0447 [ 0.7758 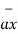 + 0.2821
+ 0.2821 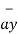 - 0.5642
- 0.5642 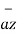 ]
]
= -0.0346 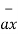 - 0.01261
- 0.01261 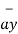 + 0.02522
+ 0.02522 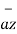 N
N
This is the required force exerted on Q2 by Q1
The magnitude of the force is
|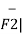 =
= 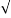 (0.0346) 2 + (0.01261 ) 2 + (-0.02522) 2 = 44.634mN
(0.0346) 2 + (0.01261 ) 2 + (-0.02522) 2 = 44.634mN
Q6) Explain Gauss law?
A6) The electric flux passing through any closed surface is equal to the total charge enclosed by that surface. The total charge enclosed by the irregular closed surface is Q coulombs. Hence the total flux has to pass through the closed surface is Q. Consider a small differential surface dS at point P. As the surface is irregular the direction of D as well as its magnitude is going from point to point on the surface. The surface dS under consideration can be represented in vector form.
d 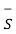 = d S
= d S 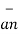
Where 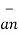 = Normal to the surface d at point P
= Normal to the surface d at point P
The flux density at point P is D and its direction is such that it makes an angle Ѳ with the normal direction at point P.
The flux d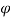 passing through the surface dS is the product of the component normal to dS and d
passing through the surface dS is the product of the component normal to dS and d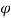 .
.
Mathematically thus can be represented as,
d 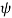 = Dn dS
= Dn dS
Dn = component of 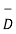 in the direction of normal to the surface dS
in the direction of normal to the surface dS
From the figure we can write
Dn = |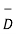 | cos
| cos 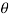
d 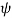 = |
= |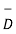 | cos
| cos 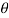 dS
dS
From the definition of the dot product
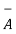 .
. 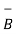 = |A| |B| cos ƟAB
= |A| |B| cos ƟAB
|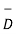 | cos
| cos 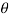 dS =
dS = 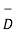 d
d 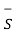
This is the flux passing through incremental surface area dS. Hence the total flux passing through the entire closed surface is to be obtained by finding the surface integration of the equation
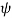 =
= 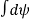 =
= 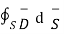
 sign indicates the integration over the closed surface called closed surface integral.
sign indicates the integration over the closed surface called closed surface integral.
Such a closed surface over which the integration in eq(6) is carried out is called Gaussian surface.
Total charge enclosed by the surface is given by
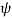 =
= 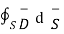 = Q = Charge enclosed.
= Q = Charge enclosed.
Q7) Explain equipotential surface?
A7) An equi potential surface is a three-dimensional surface in which the electric potential V is the same at every point.
Using the example of a single positive charge q, the expression for V is:
V=14πϵ0qrV=14πϵ0qr
If a test charge q0 is moved from point to point on an equipotential surface, the electric potential energy q0V will remain constant. In equation form, this means that the work done is 0:
W=–ΔU=–q0ΔV=0
It follows that →E must be perpendicular to the equipotential surface at every point.
We know that
DV=∂V/∂x.dx+∂V/∂ydy+∂V/∂z. Dz
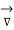 . V .
. V .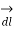
= - 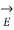 .
. 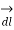
Since dV=0, 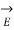 .
. 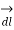 is 0 -> perpendicular.
is 0 -> perpendicular.
At each point the direction of 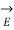 is the direction in which V decreases most rapidly.
is the direction in which V decreases most rapidly.
DV = 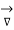 . V .
. V .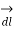
= - 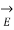 .
. 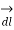
= -E dl cos ɸ
Where ɸ is the angle between electric filed and the displacement vector.
Q8) Explain Possions and Laplace Equation?
A8) Poisson’s Equation:
From the Gauss’s law in the point form Poisson’s equation can be derived. Consider the Gauss’s law in the point form as
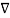 .
. 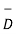 =
= 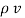
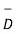 = flux density
= flux density
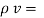 Volume charge density.
Volume charge density.
For a homogeneous isotropic and linear medium, flux density and the electric field are directly proportional. Thus,
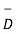 =
= 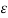 .
. 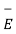
 .
. 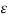 .
. 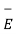 =
= 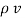
From the gradient relationship
E = - 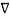 . V
. V
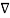 .
. 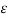 (-
(- 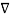 . V) =
. V) = 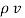
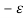 (
( 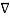 .
. 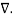 V) =
V) = 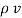
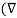 .
. 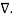 V) =-
V) =- 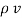 /
/ 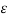
Now 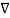 .
. 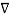 Operation is called ‘del squared’ operation denoted as
Operation is called ‘del squared’ operation denoted as 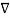 2.
2.
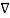 2. V = -
2. V = - 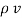 /
/ 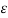
This equation is called as Poisson’s Equation
Laplace equation
If in a certain region volume charge density is zero ( 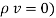 which is true for dielectric medium then the Poisson’s equation takes the form,
which is true for dielectric medium then the Poisson’s equation takes the form,
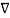 2. V =0.
2. V =0.
This equation is called Laplace’s equation.
Q9) Write a short note on capacitance?
A9) Consider two conducting materials M1 and M2 which are placed in a dielectric medium having permittivity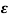 . The material M1 carries a positive charge Q while the material M2 carries a negative charge equal in magnitude as Q. There are no other charges present and the total charge of the system is zero.
. The material M1 carries a positive charge Q while the material M2 carries a negative charge equal in magnitude as Q. There are no other charges present and the total charge of the system is zero.
In conductors, charges cannot reside within the conductor and it resides only on the surface. Thus, for M1 and M2 charges +Q and -Q reside on the surfaces M1 and M2 respectively. This is shown in figure.
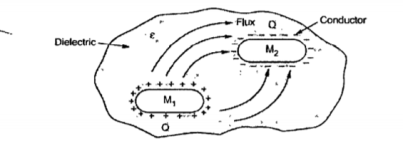
Figure 19. Capacitance
Such a system which has two conducting surfaces carrying equal and opposite charges separated by a dielectric is called capacitive system giving rise to capacitance.
The electric field is normal to the conductor surface and the electric flux is directed from M1 and M2 in such a system. There exists a potential difference between the two surfaces of M1 and M2. Let this potential be V12. The ratio of magnitudes of the total charge on any one of the two conductors and the potential difference between the conductors is called capacitance of the two conductor system denoted as C.
C = Q/ V12
In general C =Q/V
Where Q = charge in coulombs
V = Potential difference in volts.
The capacitance is measured in farads.
Q10) Explain uniqueness theorem?
A10) Assume that the Laplace’s equation has two solutions say V1 and V2 both are the function of the coordinate system. These solutions must satisfy Laplace equation hence we write,
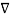 2 V1 =0 and
2 V1 =0 and 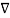 2 2 =0 -----------------------------------------(1)
2 2 =0 -----------------------------------------(1)
Both the solutions must satisfy the boundary conditions as well. At the boundary the potentials at different points are the same due to equipotential surface then
V1 = V2
Let the solution between the two solutions be Vd
Vd = V2 – V1 ---------------------------------------------------------------------(3)
Using Laplace’s equation for the difference Vd
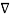 2Vd =
2Vd = 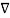 2 (V2-V1) =0 -----------------------------------------------------------(4)
2 (V2-V1) =0 -----------------------------------------------------------(4)
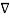 2 V2 =
2 V2 = 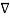 2 V1 =0 -------------------------------------------------------------------(5)
2 V1 =0 -------------------------------------------------------------------(5)
On the boundary Vd =0 from eq(2) and (3)
Now the divergence theorem states that
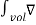 .
. 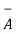 dv =
dv = 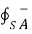 . d
. d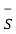 ---------------------------------------------------------(6)
---------------------------------------------------------(6)
Let 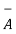 = Vd
= Vd 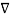 Vd from vector algebra
Vd from vector algebra
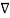 . (
. (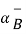 ) =
) = 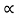 (
(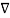 .
. 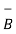 ) +
) + 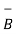 .(
.( 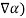
Now use this for 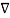 (Vd
(Vd 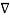 Vd) with
Vd) with 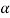 =Vd and
=Vd and 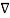 . Vd =
. Vd = 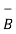
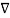 (Vd
(Vd 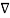 Vd) = Vd (
Vd) = Vd (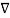 .
.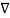 . Vd) +
. Vd) + 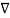 Vd . (
Vd . (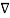 Vd) --------------------------------(7)
Vd) --------------------------------(7)
But 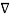 .
.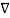 =
= 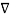 2
2
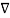 (Vd
(Vd 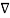 Vd) =
Vd) = 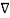 Vd .
Vd .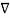 Vd ----------------------------------------------(8)
Vd ----------------------------------------------(8)
To use this in equation(6) let A= Vd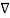 Vd hence
Vd hence
= 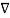 Vd .
Vd .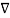 Vd =
Vd = 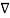 .
. 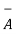 =
= 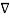 Vd .
Vd .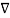 Vd --------------------------------------(9)
Vd --------------------------------------(9)
But Vd =0 on boundary hence the RHS eq(9) is zero.
Therefore
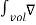 Vd .
Vd .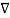 vd dv =0 ---------------------------------------------------(10)
vd dv =0 ---------------------------------------------------(10)
This the volume integral to be evaluated on the volume enclosed by the boundary.
It is known that ,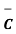 .
. 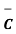 = |
= | 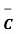 | 2
| 2
Therefore
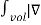 Vd |2 dv =0 as
Vd |2 dv =0 as 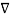 Vd is vector.----------------------------------(11)
Vd is vector.----------------------------------(11)
Now integration can be zero under two conditions:
(1) The quantity under the integral sign is zero.
(2) The quantity is positive in some regions and negative in some regions by an equal amount and hence zero.
But the squared term cannot be zero in any region hence quantity under integral must be zero.
|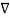 Vd 2 | =0
Vd 2 | =0
That is 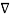 Vd =0
Vd =0
As the gradient of d isV2-V1 is zero means V2-V1 is constant and not changing with any of the coordinates . But considering boundary it can be proved that V2 – V1 =0 .
Therefore V2 =V1
This proves that both the solutions are equal and cannot be different. Thus, Uniqueness Theorem states that:
If the solution of Laplace’s equation satisfies the boundary condition, then that solution is unique by whatever method it is obtained.
The solution of Laplace’s equation gives the filed which is unique satisfying the same boundary condition in each region.