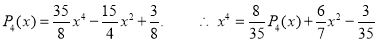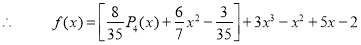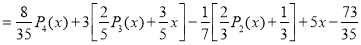Unit 1

Polynomials

Q1)

Show that for any function, which the nth derivative is continuous,

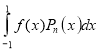
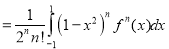
A1)Using Rodrigue’s Formula:

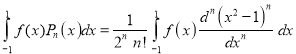[Integrate by parts]

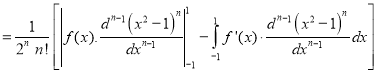
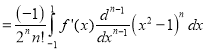
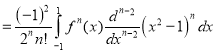[Again integrating by parts]

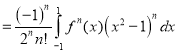      [Integrating by parts (n - 2) times]

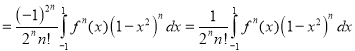
Q2)

Assuming that a polynomial of degree n can be written as

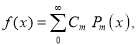
Show that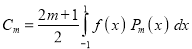

A2)

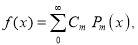
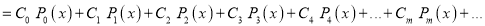
Multiplying both sides by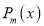we get

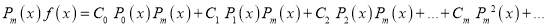
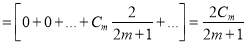
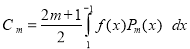
Q3)

Prove that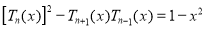     

A3)

Let

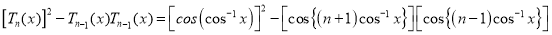
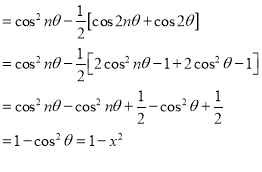
Q4) Prove that (a) 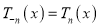   (b)

   (c)

A4) The Chebyshev polynomial of degree n over the integral [-1, 1] is define as -

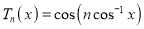…. (1)

(a) On putting –n for n in (1) we get

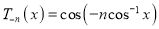
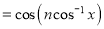
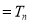
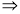
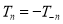
(b)  Let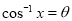 so that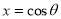

On Putting 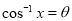in (1), it becomes

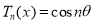…. (2)

(c) If 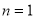on putting 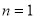in (1) we get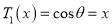

Q5)

Prove that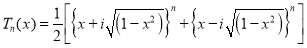  

A5)

We know that 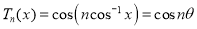…. (1)

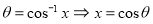
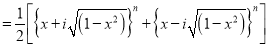
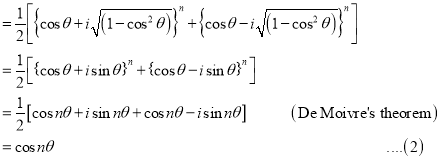
From (1) and (2) we have

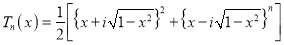
Q6)

Prove that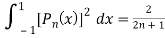

A6)

We know that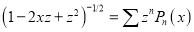

Squaring both sides, we get

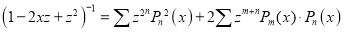
Integrating both sides between -1 and 1 we have

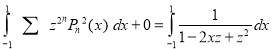
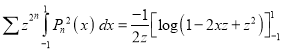
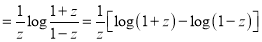
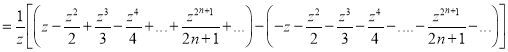
Equating the coefficient of 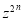on both sides, we have

Hence

Q7) Express 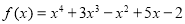in terms of Legendre polynomials.

A7)

Since