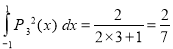Unit 2
Sets, relations and functions
Q1)
Solve the recurrence relation
where
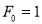and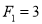 
A1)
The characteristic equation of the recurrence relation is -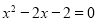
Hence the roots are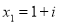 
and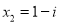 
In polar form,
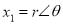and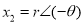
, where 
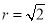and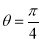 
The roots are imaginary so, this is in the form of case 2.
Hence the solution is
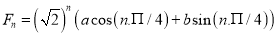
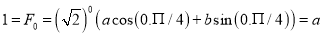
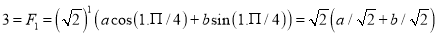
Solving these equations, we get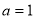 
and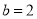 
Hence the final solution is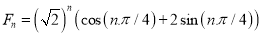 
Q2) Given three sets P, Q and R such that:
P = {x: x is a natural number between 10 and 16},
Q = {y: y is a even number between 8 and 20} and
R = {7, 9, 11, 14, 18, 20}
(i) Find the difference of two sets P and Q
(ii) Find Q - R
(iii) Find R - P
(iv) Find Q – P
A2)
According to the given statements:
P = {11, 12, 13, 14, 15}
Q = {10, 12, 14, 16, 18}
R = {7, 9, 11, 14, 18, 20}
(i) P – Q = {those elements of set P which are not in set Q}
= {11, 13, 15}
(ii) Q – R = {those elements of set Q not belonging to set R}
= {10, 12, 16}
(iii) R – P = {Those elements of set R which are not in set P}
= {7, 9, 18, 20}
(iv) Q – P = {Those elements of set Q not belonging to set P}
= {10, 16, 18}
Q3) If A = { 1, 3, 5} and B = {2, 3}, then
Find: (i) A × B (ii) B × A (iii) A × A (iv) (B × B)
A3)
A ×B={1, 3, 5} × {2,3} = [{1, 2},{1, 3},{3, 2},{3, 3},{5, 2},{5, 3}]
B × A = {2, 3} × {1, 3, 5} = [{2, 1},{2, 3},{2, 5},{3, 1},{3, 3},{3, 5}]
A × A = {1, 3, 5} × {1, 3, 5}= [{1, 1},{1, 3},{1, 5},{3, 1},{3, 3},{3, 5},{5, 1},{5, 3},{5, 5}]
B × B = {2, 3} × {2, 3} = [{2, 2},{2, 3},{3, 2},{3, 3}]
Q4)
Show that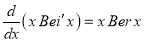 
A4)
We know that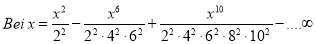 
… (1)
On differentiating (1) w.r.t ‘x’ we get
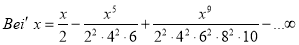
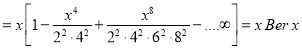
Q5) Show that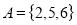 
and set 
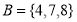are disjoint sets.
A5) Given
Set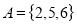 
Set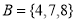 
To prove: Set A and Set B are disjoint.
Proof: Two sets are disjoint if their intersection results to the null set.
Therefore,
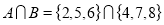
As you can see, A and B do not have any common element.
So,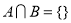 
Hence proved A and B are disjoint.
Q6)
Solve the recurrence relation -
where 
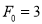and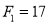
A6)
The characteristic equation of the recurrence relation is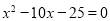 
So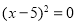 
Hence there is single real root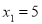 
As there is single real valued root, this is in the form of case 2
Hence the solution is -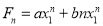 
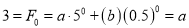
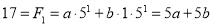
Solving these two equations, we get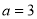 
and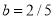
Hence the final solution is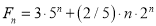 
Q7)
Assuming that a polynomial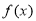 
of degree n can be written as
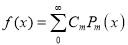. Show that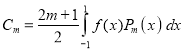 
A7)
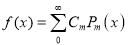
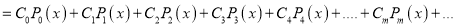
Multiplying both sides by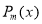
, we get
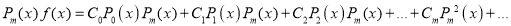
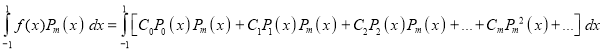
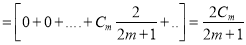
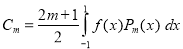
Q8) If A × B = {(p, x); (p, y); (q, x); (q, y)}, find A and B.
A8)
A is a set of all first entries in ordered pairs in A × B.
B is a set of all second entries in ordered pairs in A × B.
Thus A = {p, q} and B = {x, y}
Q9)
Prove that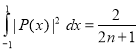 
A9) We know that 
Squaring both sides we get
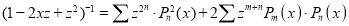
Integrating both sides between -1 and 1, we have
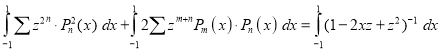
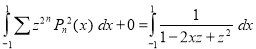
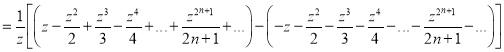
Equating the coefficient of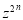 
on both sides, we have
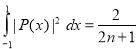
Hence
