Unit 3

Introduction to Graphs

Q1)

In directed graph find indegree and outdegree.

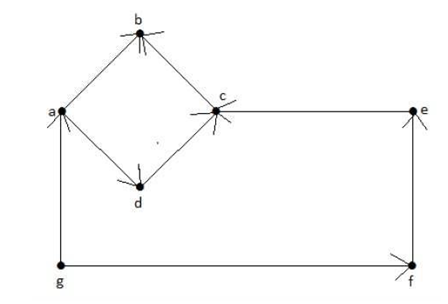
A1)

Q2) Find Eccentricity of a Vertex in given graph.

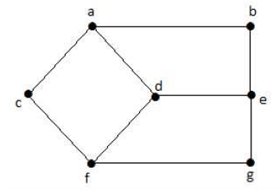
A2)

In the above graph, the eccentricity of ‘a’ is 3.

The distance from ‘a’ to ‘b’ is 1 (ab’)

From ‘a’ to ‘c’ is 1(‘ac’),

From ‘a’ to ‘d’ is 1 (‘ad’),

From ‘a’ to ‘e’ is 2 (‘ab’-’be’) or (‘ad’-’de’),

From ‘a’ to ‘f’ is 2 (‘ac’-‘cf’) or (‘ad’-‘df’),

From ‘a’ to ‘g’ is 3 (‘ac’-‘cf’-‘fg’) or (‘ad’-‘df’-‘fg’)

So the eccentricity is 3, which is a maximum from vertex ‘a’ from the distance between ‘ag’ which is maximum.

In other words,

e(b) =3

e(c) =3

e (d) =3

e(e) =3

e(f)=3

e(g)=3

Q3) Find distance between two vertices in given graph

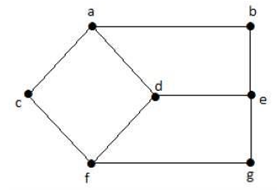
A3)

Here, the distance from vertex‘d’ to vertex ‘e’ or simply ‘de’ is 1 as there is one edge between them. There are many paths from vertex‘d’ to vertex ‘e’-

• Da, ab, be
• Df, fg, ge
• De (It is considered for distance between the vertices
• Df, fc, ca, ab, be
• Da, ac, cf, fg, ge

Q4) Write Euler’s Path & explain with graph

A4)

An Euler’s path contains each edge of ‘G’ exactly once and each vertex of ‘G’ atleast once A conncected graph G is said to be traversible if it contains an Euler’s path.

Euler’s Path=d-c-a-b-d-e.

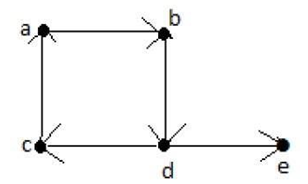
Q5) Write Euler’s circuit theorem & explain with graph

A5)

A connected graph ‘G’ is traversable if and only if the number of vertices with odd degree in G is exactly 2 or 0. A connected graph G can contain an Euler’s path, but not an Euler’s circuit if it has exactly two vertices with an odd degree.

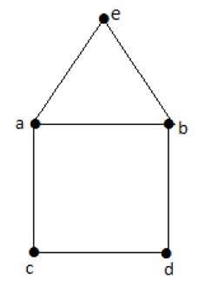
Note: This Euler path begins with a vertex odd degree and ends with other vertex of odd degree.

Euler’s path – b-e-a-b-d-c-a is not an Euler’s circuit, but it is an Euler’s path. Clearly it has exactly 2 odd degree vertices.

Note: In a connected graph G, if the number of vertices with odd degree=0, then Euler’s circuit exists.

Q6) What is cyclic graph and draw its graph.

A6)

A graph with at least one cycle is called a cyclic graph

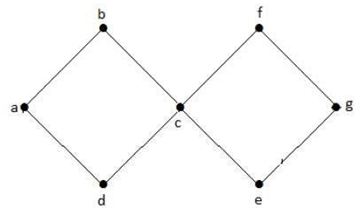
In the graph, we have two cycles a-b-c-d-a and c-f-g-e-c. Hence it is called a cyclic graph.

Q7) Which of the following are isomorphic?

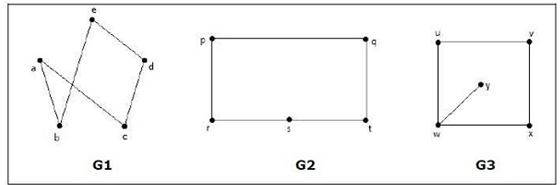
A7)

In the graph, vertex ‘w’ has only degree 3, whereas all the other graph vertices has degree 2. Hence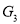not isomorphic to 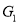or.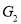

Taking compliments of 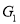and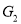, we have

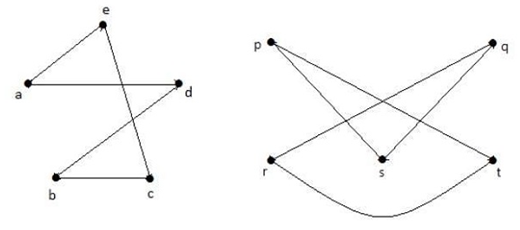
Here 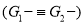, hence .

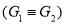Q8) What is Spanning Trees ?

A8) Let G be a connected graph, then the sub-graph H of G is called a spanning tree of G if

• H is a tree
• H contains all vertices of G

A spanning tree T of an undirected graph G is a subgraph that includes all of the vertices of G.

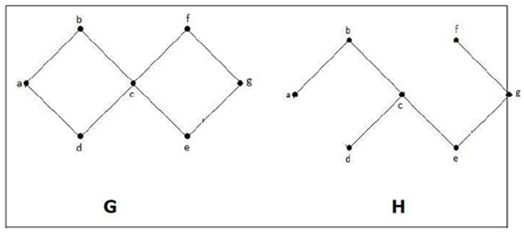
In the above graph, G is a connected graph and H is a subgraph of G.

Clearly, the graph H has no cycles, it is a tree with six degrees which is one less than the total number of vehicles. Hence H is the spanning tree of G.