Unit 4
Basic Statistics
Q1) Find the arithmetic mean for the following distribution:
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
A1)
Let assumed mean 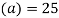
Class | Mid-value 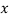 | Frequency  | 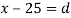 | 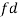 |
0-10 10-20 20-30 30-40 40-50 | 5 15 25 35 45 | 7 8 20 10 5 | -20 -10 0 10 5 | -140 -80 0 100 100 |
Total |
|
| 50 | -20 |
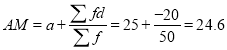
Q2)
Find the value of Median from the following data.
No.of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
No.of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
A2) The given cumulative frequency distribution will first be converted into ordinary frequency as under
Class Interval | Cumulative frequency | Ordinary frequency |
0-5 5-10 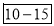 15-20 20-25 25-35 30-35 35-40 40-45 | 29 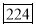 465 582 634 644 650 653 655 | 29=29 224-29=195 465-224=  582-465=117 634-582=52 644-634=10 650-644=6 653-650=3 655-653=2 |
Median= size of  or 327.5th item
or 327.5th item
327.5th item lies in 10-15 which is the median class.
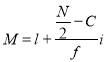
Where 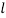 stands for lower limit of median class,
stands for lower limit of median class,
N stands for the total frequency,
C stands for the cumulative frequency just preceding the median class,
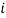 stands for class interval
stands for class interval
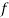 stands for frequency for the median class.
stands for frequency for the median class.
Median

Q3)
Find the mode from the following data:
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
A3)
Age | Frequency | Cumulative frequency |
0-6 6-12 12-18 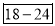 24-30 30-36 36-42 | 6 11 25 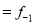 35 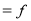 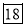 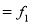 12 6 | 6 17 42 77 95 107 113 |
Mode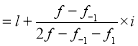
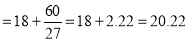
Q4)
Find the mean deviation of the following frequency distribution.
Class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
A4)
Let 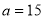
Class | Mid value 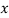 | Frequency 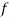 | 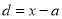 |  | 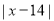 | 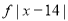 |
0-6 6-12 12-18 18-24 24-30 | 3 9 15 21 27 | 8 10 12 9 5 | -12 -6 0 6 12 | -96 -60 0 54 60 | 11 5 1 7 13 | 88 50 12 63 65 |
Total |
| 44 |
| -42 |
| 278 |
Mean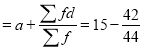
Average deviation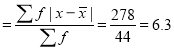
Q5)
The first four moments about the working mean 28.5 of a distribution 0.294, 7.144, 42.409 and 454.98. Calculate the moments about the mean. Also evaluate 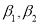 and comment upon the skewness and kurtosis of the distribution.
and comment upon the skewness and kurtosis of the distribution.
A5)
The first four moments about the arbitrary origin 28.5 are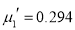 ,
, 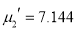 ,
, and
and 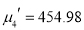 .
.

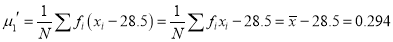 or
or 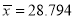
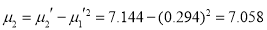
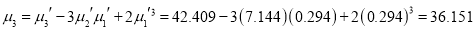
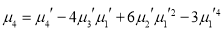

Now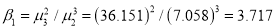
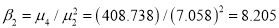

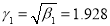 which indicates considerable skewness of the distribution.
which indicates considerable skewness of the distribution.
 which shows that the distribution is leptokurtic.
which shows that the distribution is leptokurtic.
Q6) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 item, now 60, at least 7 will live to be 70?
A6)
The probability that a man aged 60 will live to be 70

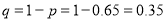
Number of men
Probability that at least 7 men will live to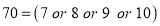
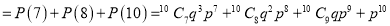
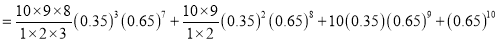
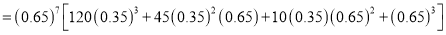
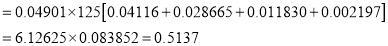
Q7) A die is thrown 8 times and it is required to find the probability that 3 will show (i) Exactly 2 times
(ii) At least seven times (iii) At least once.
A7)
The probability of throwing 3 in a single trial =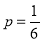
The probability of not throwing 3 in a single trial 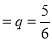
(i) P(getting 3 exactly 2 times)=P (getting 3, at 7 or 8 times) 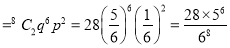
(ii) P (getting 3, at least seven times)=P (getting 3, at 7 or 8 times) 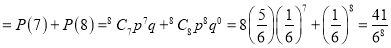
(iii) P (getting 3 at least once)
=P (getting 4, at 1 or 2 or 3 or 4 or 5 or 6 or 7 or 8 times)
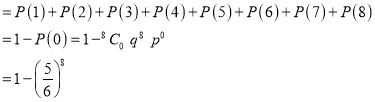
Q8) Assume that the probability of on individual coalminer being killed in a mine accident during a year is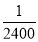 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 metres, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 metres, there will be at least one fatal accident in a year.
A8)
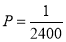 ,
,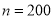
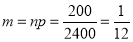
P(At least one)=P(1 or 2 or 3 or …. Or 200)
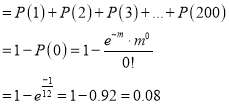
Q9) In a certain factory producing cycle tyres there is a small chance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution calculate the approximate number of lots containing no defective, one defective and two defective tyres, respectively, in a consignment of 10000 lots.
A9)

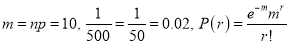
S.No | Probability of defective | Number of lots containing defective |
1 | 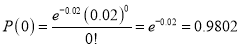 | 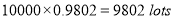
|
2 |  | 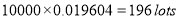
|
3 | 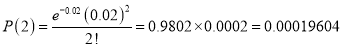 | 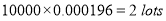
|
Q10) Find the area under the normal curve in each of the cases.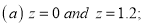
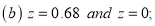
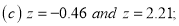

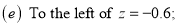
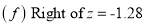
A10)
(a) Area between  and
and  (b) Area between
(b) Area between 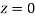 and
and 
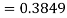
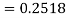
(c) Required area 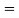 (Area between
(Area between 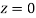 and
and 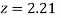 )+
)+
(Area between 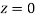 and
and 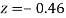 )
)
=(Area between  and
and  )
)
+(Area between 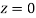 and
and 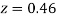 )
)
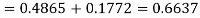
(d) Required area 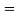 (Area between
(Area between  and
and 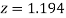 ) – (Area between
) – (Area between  and
and 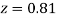 )
)
(e) Required area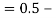 (Area between
(Area between 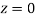 and
and 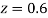 )
)
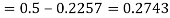
(f) Required area = (Area between 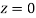 and
and 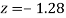 )
)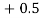
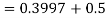
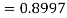
Q11) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 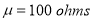 and standard deviation
and standard deviation 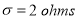 What percentage of resistors will have resistance between 98 ohms and 102 ohms?
What percentage of resistors will have resistance between 98 ohms and 102 ohms?
A11)
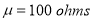

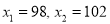
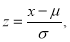
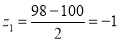
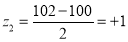
Area between 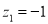 and
and 
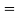 (Area between
(Area between 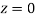 and
and  )+(Area between
)+(Area between 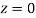 and
and 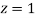 )
)
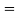 (Area between
(Area between 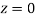 and
and  )=2
)=2 0.3413=0.6826
0.3413=0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms =68.26