Unit 5

Applied Statistics

Q1) By the method of least squats, find the straight line that best fits the following data:

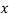	1	2	3	4	5
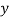	14	27	40	55	68

A1)  Let the equation of the straight line best fit be 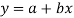 …. (1)

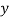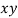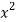1	14	14	1
2	27	54	4
3	40	120	9
4	55	220	16
5	68	340	25

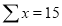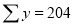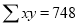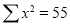Normal equations are

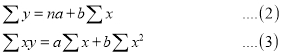
On Putting the values of in (2) and (3), we have

On solving (4) and (5), we get

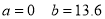
On Substituting the values of a and b in (1), we get

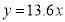
Q2) Eleven students were given a test in statics. They were given a month’s further tuition and a second test of equal difficulty was held at the end of it. Do the marks give evidence that the students have benefitted by extra coaching?

A2) We compute the means and the S.D. Of the difference between the marks of the two tests as under:

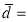mean of d’s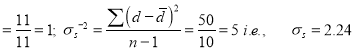

Assuming that the students have not been benefited by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e., .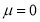

Then 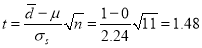nearly and

Students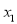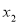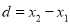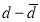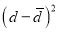
1	23	24	1	0	0
2	20	19	-1	-2	4
3	19	22	3	2	4
4	21	18	-3	-4	16
5	18	20	2	1	1
6	20	22	2	1	1
7	18	20	2	1	1
8	17	20	3	2	4
9	23	23	-	-1	1
10	16	20	4	3	9
11	19	17	-2	-3	9

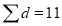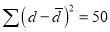From table IV, we find that 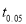(for 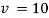)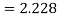. As the calculated value of 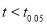, the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefited by extra coaching.

Q3) Fit a second degree parabola to the following data by least squares method.

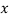	1929	1930	1931	1932	1933	1934	1935	1936	1937
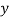	352	356	357	358	360	361	361	360	359

A3) Taking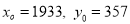

Taking

The equation 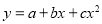is transformed to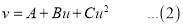

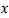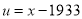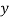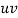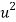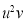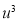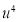1929	-4	352	-5	20	16	-80	-64	256
1930	-3	360	-1	3	9	-9	-27	81
1931	-2	357	0	0	4	0	-8	16
1932	-1	358	1	-1	1	1	-1	1
1933	0	360	3	0	0	0	0	0
1934	1	361	4	4	1	4	1	1
1935	2	361	4	8	4	16	8	16
1936	3	360	3	9	9	27	27	81
1937	4	359	2	8	16	32	64	256
Total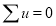

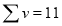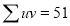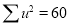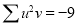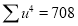Normal equations are

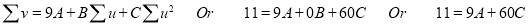
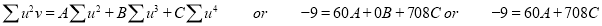
On solving these equations, we get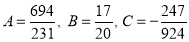

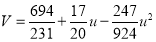
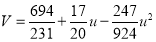
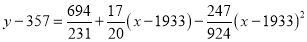
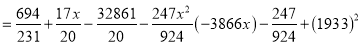
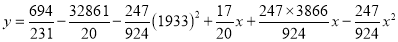
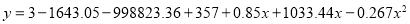
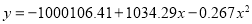
Q4) Fit a second-degree parabola to the following data:

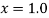	1.5	2	2.5	3	3.5	4
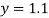	1.3	1.6	2	2.7	3.4	4.1

A4)

We shift the origin to (2.5, 0) and take 0.5 as the new unit. This amounts to changing the variable 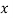to X, by the relation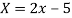

Let the parabola of fit be 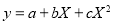. The values of 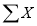etc., as calculated below:

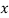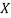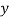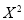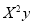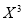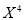1.0	-3	1.1	-3.3	9	9.9	-27	81
1.5	-2	1.3	-2.6	4	5.2	-8	16
2.0	-1	1.6	-1.6	1	1.6	-1	1
2.5	0	2	0	0	0	0	0
3.0	1	2.7	2.7	1	2.7	1	1
3.5	2	3.4	6.8	4	13.6	8	16
4.0	3	4.1	12.3	9	36.9	27	81
Total	0	16.2	14.2	28	69.9	0	196

The normal equations are

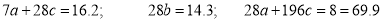
Solving these as simultaneous equations, we get

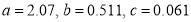
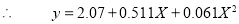
Replacing X by 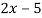in the above equation, we get

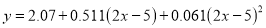
Which simplifies by 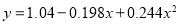. This is the required parabola of best fit.

Q5) A coin was tossed 400 times and the head turned up 216 times. Test the hypothesis the coin unbiased at 5% level of significance.

A5) Suppose the coin is unbiased.

Then the probability of getting the head in a toss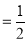

• Expected number of successes
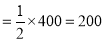
• Thus the excess of observed value over expected value = 216 – 200 = 16
• Also S.D. Of simple sampling

Hence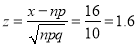

As,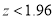 the hypothesis is accepted at 5% level of significance i.e., we conclude that the coin is unbiased at 5% level of significance.

Q6) In a city A 20% of a random sample of 900 school boys had a certain slight physical defect. In another city B, 18.5% of random sample of 1600 school boys had the same defect. Is this difference between the proportions significant?

A6) We have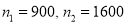

And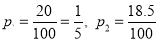

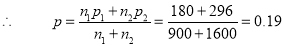
And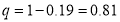

Thus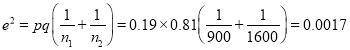

Giving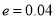 nearly

Also

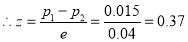
As 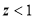, the difference between the proportions is not significant.

Q7) One type of aircraft is found to develop engine trouble in 5 flights out of a total of 100 and another type in 7 flights out of a total of 200 flights. Is there a significant difference in the two types of aircrafts so far as engine defects are concerned.

A7) 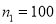flights, Number of troubled flights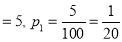

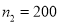flights, Number of troubled flights

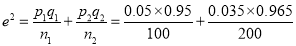
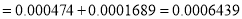
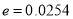
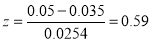
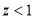, Difference is not significant.

Q8) A certain stimulus administered to each 12 patients resulted in the following increases of blood pressure: 5, 2. 8, -1, 3, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure.

A8)

Let us assume that the stimulus administered to all the 12 patients will increase the B.P. Taking the population to be normal with mean 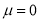and S.D.,

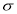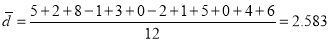
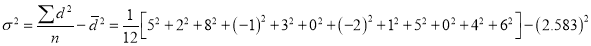
Now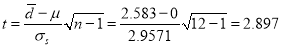

Here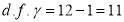

For 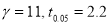, from table IV.

Since the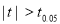, our assumption is rejected i.e., the stimulus does not increase the B.P.

Q9) From a random sample of 10 pigs fed on diet A, the increases in weight in a certain period were 10, 6, 16, 17, 13, 12,8, 14,15, 9 lbs. For another random sample of 12 pigs fed on diet B, the increases in the same period were 7,13, 22, 15, 12, 14, 18, 8, 21, 23, 10, 17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight?

A9) We calculate the means and standard deviations of the sample as follows:

	Diet A			Diet B
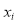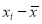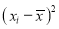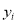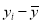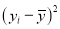10	-2	4	7	-8	64
6	-6	36	13	-2	4
16	4	16	22	7	49
17	5	25	15	0	0
13	1	1	12	-3	9
12	0	0	14	-1	1
8	-4	16	18	3	9
14	2	4	8	-7	49
15	3	9	21	6	36
9	-3	9	23	8	64
			10	-5	25
			17	2	4
120	0	120	180	0	314

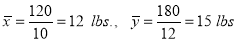
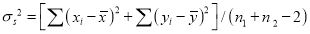
Assuming that the samples that the samples do not differ in weight so far as the two diets are connected i.e.,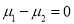

Hence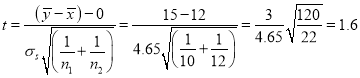 nearly

Here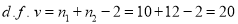

For 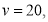we find 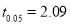[From table IV]

the calculated value of .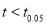

Hence the difference between the sample means is not significant i.e., the two diets do not differ significantly as regards their effect on increase in weight.

Q10) The nine items of a sample have the following values: 45, 47, 50, 52, 48, 47, 49, 53, 51. Does the mean of these differ significantly from the assumed mean of 47.5?

A10) We find the mean and standard deviation of the sample as follows:

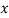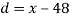45	-3	9
47	-1	1
50	2	4
52	2	4
48	0	0
47	-1	1
49	1	1
53	5	25
51	3	9
Total	10	66

mean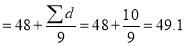

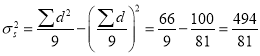
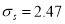
Hence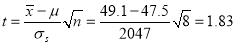

Here

For  , we get table IV,

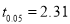
As calculated value of 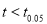,the value of t is not significant at 5% level of significance which implies that there is no significant difference between 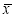and 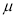 . Thus the test provides no evidence against the provides no evidence against the population mean being 47.5.