Unit – 2 | unit 2 system modelling in terms of differential equations

Back to Study material

Network Theory

Unit – 2

System modelling in terms of differential equations

Q1)

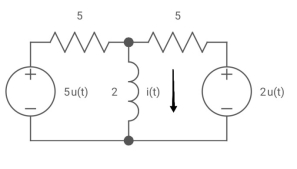
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_221139.jpg$

V0 (t) = ? t =o if capacitor is uncharged?

A1)

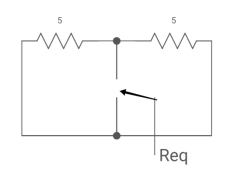
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_221439.jpg$

Req = R1R2 /R1+R2

V0(0)=0

V0 (infinity) = VR R2/R1+R2

V0 (t) = V0 (infinity) + [Vo (0) – V0 (infinity)] e-t/c

=VR R2/R1+R2 *[ 1- e+(R1+R2)/R1R2]

Q2)

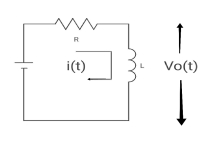
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_204756.jpg$

A2)

Time constant , c= L/Req = L/R

V(infinity) = 0

V(0) = VR

I(infinity) = VR/R, I (0) =0

By KVL,

VR=i(t) R + L di/dt(t)

On solving

V0(t)= VR e-tR/L

Q3) Find i(t)

For t>0?

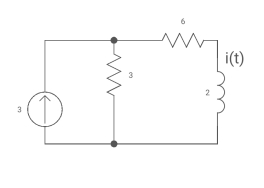
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_203051.jpg$

A3)

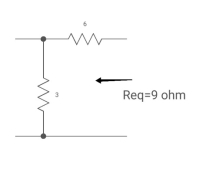
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_203715.jpg$

Req = 673

= 9ohm

Diagram

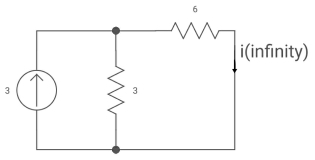
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_203820.jpg$

T= L/Req = 2/9 sec

I(0) =0

I(infinity) = 3*3/6+3 = 1A

i(+) = 1 [1-e4.51]

Q4) Capacitor is initially uncharged find

Vc (t); t >0

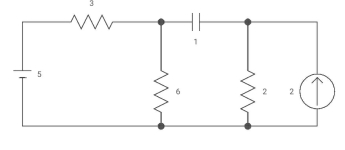
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_220353.jpg$

A4)

Diagram

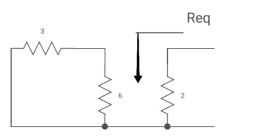
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_220316.jpg$

Req = (3116)+2

=2+2 = 4ohm

C= c Req

= 2 sec

Clearly Vc(0) =0

Diagram

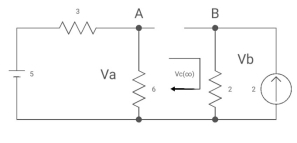
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_220240.jpg$

By voltage divides, VA = 5*6/3+B = 30 v/9

Clearly by ohms low

VB = 2*2 = 4v

Apply KVL, VA-Vc-VB =0

Vc(infinity) = 30/9 – 4 = -2/3 V

Vc (t) = -2/3 [1- e0.5t]

CURVE:-

Diagram

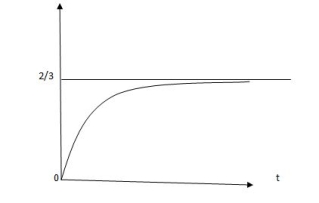
$C:\Users\TARUNA\Desktop\qq\9.JPG$

Vc(t) =2/3 [1-e-0.25]

Diagram

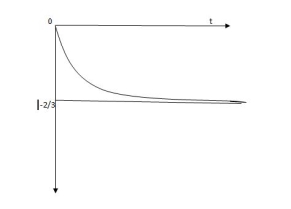
$C:\Users\TARUNA\Desktop\qq\544.JPG$

Vc(t) = -2/3 [1-e]

Q5) Find i(t)?

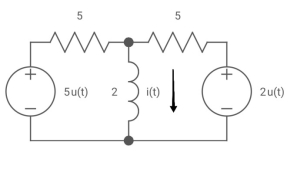
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_221139.jpg$

A5)

We know i(t) = I (infinity) +[i(0)- i(infinity0] e-t/c

Diagram

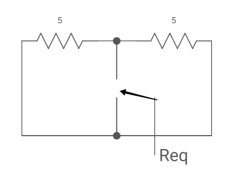
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_221439.jpg$

Req = 5*5/5+5 = 5?2 ohm

:. T=L/Req = 4/5 sec

Also, i( 0) =0

i(infinity) = u(t) +2/5 u(t)

:. I(t) = 1.4 [1-e-5/4t)]u(t)

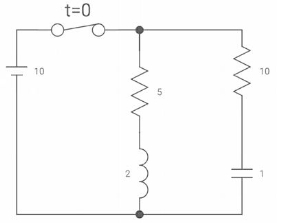
Q6)

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_181102.jpg$

If switch ‘s’ closed at t= 0 find out the voltage across capacitor and current through capacitor at t= 0+?

A6)

At t= 0- switch was open so,

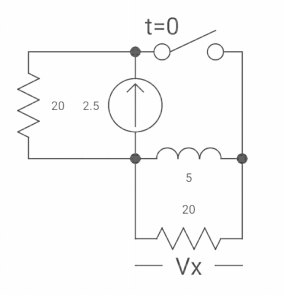
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_175854.jpg$

:. There is no potential so Vc(0-) = 0

At t= 0+, Vc (0-) = Vc(0+) = 0

Diagram

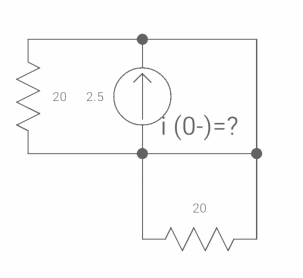
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_181034.jpg$

Isc = 10/5 = 2 A

Q7)

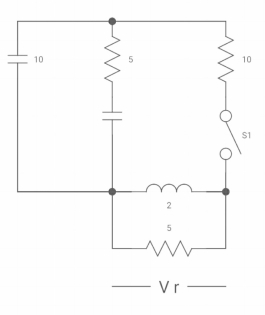
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_182433.jpg$

The switch was closed for long time before

Opening at t=0- find VX (0+) ?

(a) 25V (b) 50 V (c)-50V (d) 0V

A7)

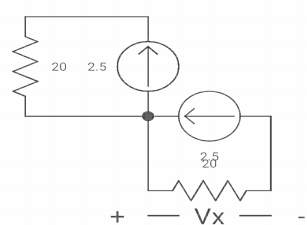
At time t=0-

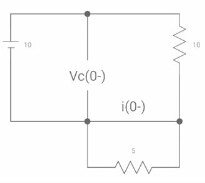
$C:\Users\TARUNA\Desktop\qq\3.JPG$

Clearly, il(0-) = 2.5 A

At t= 0+ , as inductor is initially charges

So il (0-) = il(0+)

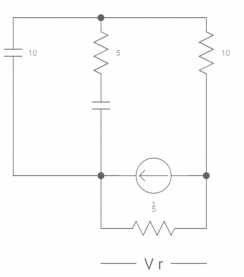
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_182547.jpg$

-VX= 20/2.5 20*2.5

VX= -50A

Q8)

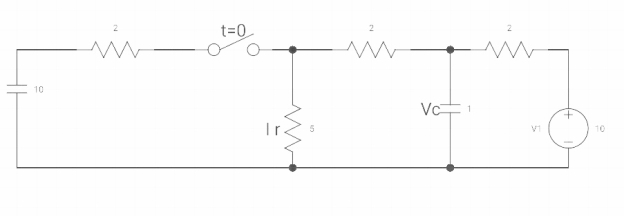
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_183527.jpg$

VR(0+)=

Dil/dt(t) = 0+ ?

If switch is opened at t= 0?

A8)

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_190915.jpg$

At t=0-

Vc(0-) = 10V

IL(0-) = 10/10 = 1 A

Also, iL(0-) = iL(0+) = 1A

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_190932.jpg$

VR(0+) = 5V

Ldi(t)/dt = VL (t)

DiL(t)/dt = VL(t)/L

At t= 0+

d/dt iL (0+) = VL(0+)/L

-VL (0+)-VR =0

VL (0+) = -5V

Dt(t) at t = ot = vl (ot)/L

=-5/2

dil/dt(o+) = 2.5 A/s

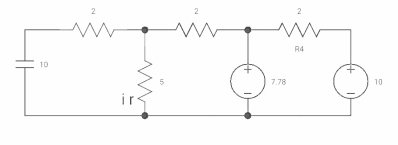
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_190932.jpg$

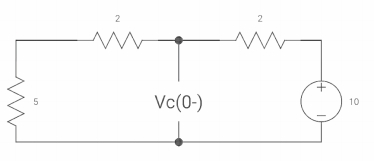
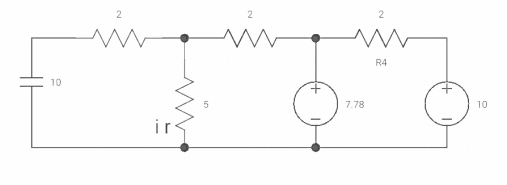
Vc(o+) and iR (o+) it switch ‘s’ is closed at t=0?

At t=0

$C:\Users\TARUNA\Desktop\qq\5.JPG$

As capacitor is fully charged so acts as

Vc (0-) = 7*10/7+2 = 70/9v

At t=0+

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_191007.jpg$

Vc(0+) = Vc (0) = 40/9v

By applying kcl at A,

VA-10/2+ VA/5+VA-7019/2 =0

VA [1/5+1/2+1/2] = 5+35/9

Va [6/5] = 80/9

Va= 400/54v

IR (0+) = Va/5 = 400/54*5 = 80/54 A

Q9)

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_221139.jpg$

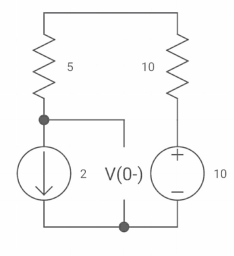
V0 (t) = ? t =o if capacitor is uncharged?

A9)

We know i(t) = i()+[ i(0)- i()]

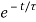
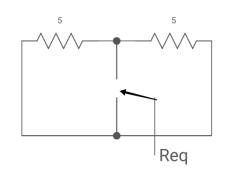
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_221439.jpg$

Req = R1R2 /R1+R2=(5x5)/(5+5)=5/2ohm

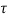=L/Req=4/5 sec

i(0)=0

i(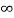)=u(t)+u(t)=1.4u(t)

i(t)=1.4[1-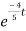]u(t)

Q10) Find V0(t)?

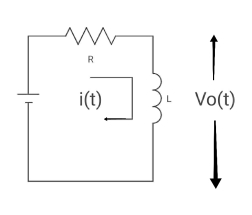
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_204756.jpg$

A10)

Time constant 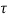=L/Req = L/R

V(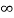) = 0, V(0)=VR(supply voltage)

i (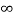) = VR/R, i(0) =0

By KVL,

VR=i(t) R + L di/dt(t)

On solving

V0(t)= VR e-tR/L

Q11) If V1=6cos2t, find i2 at steady state.

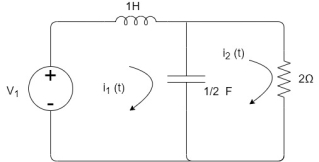
A11)

Apply KVL

6-sI1(s)-2I2(s)=0

-2I2(s)-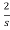I2(s)+ 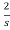I1(s)=0

I2(s)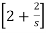= I1(s)

I1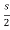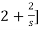(s)=[I2(s)

Substituting I1(s) in first equation

6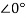-s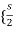[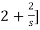}I2(s)- 2I2(s)=0

Solving above equation we get

I2(s)=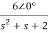

Replace s=jω, s=2j

I2(jω)===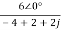

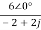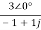
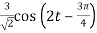
Q12) If V1=2sin2t, Va at steady state will be?

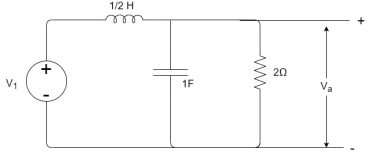
A12)

Zeq=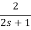

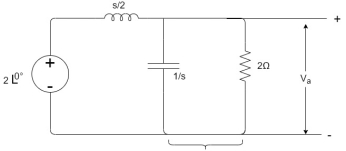
By voltage divider rule Va=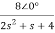

Replace s by jω , s=2j

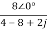Va==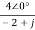

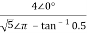
Va=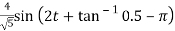

Q13) Write equation for given waveform

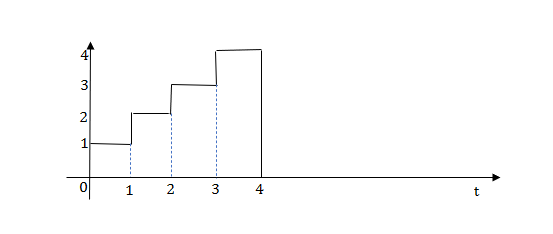
A13)

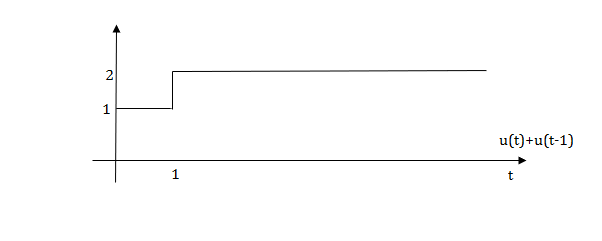
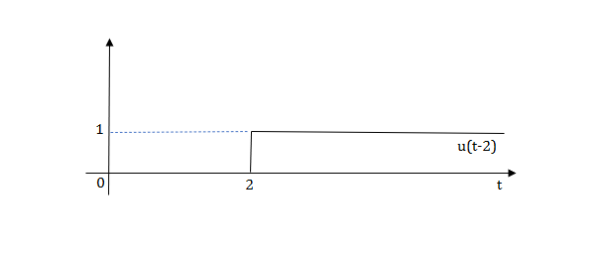
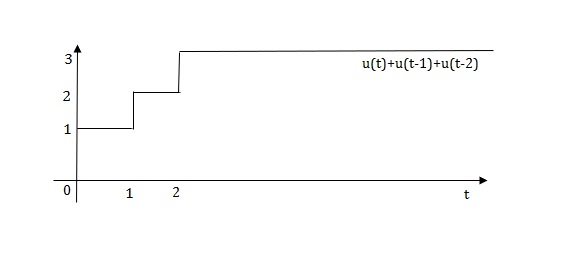
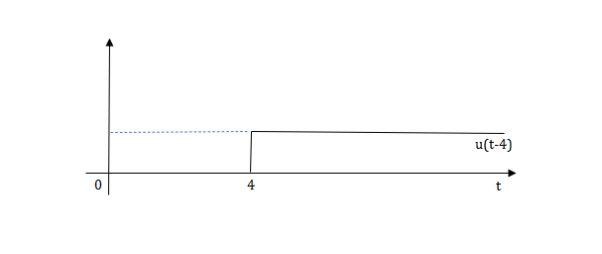
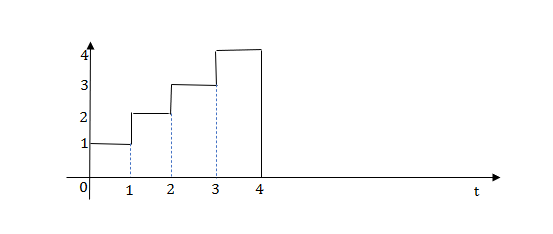
The final equation is=u(t)+u(t-1)+u(t-2)+u(t-3)-4u(t-4)

Q14) Write the equation for the given waveform?

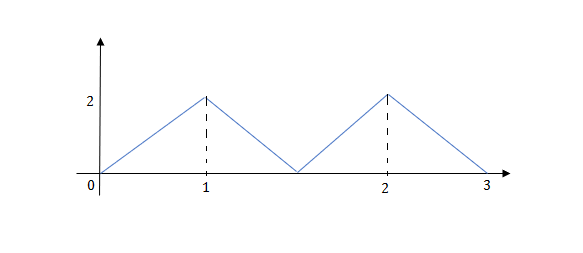
A14)

Calculating slope of above waveform

Slope for (0,0) and (1,2)

a1 slope=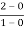=2

a2 slope=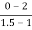=-4

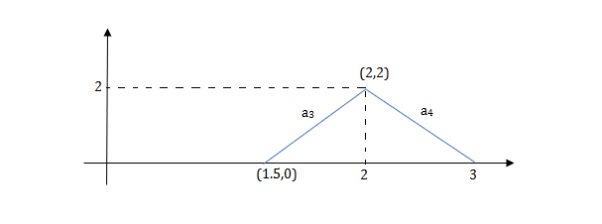
a3 slope =4 and a4= -2

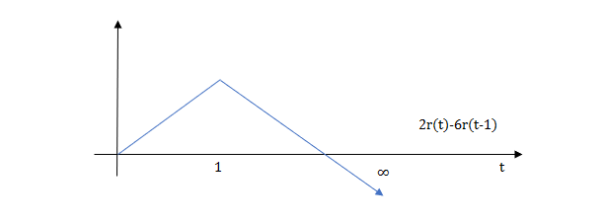
At t=1 slope changes from 2 to -4 so we need to add -6r(t-1) to 2r(t) to get the slope of -4.

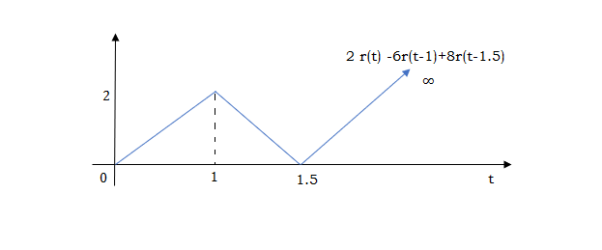
At t=1.5 slope changes from -4 to 4 so adding 8r(t-1.5) to get slope of 4

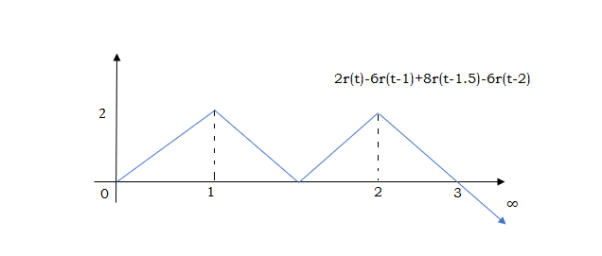
At t=2 slope changes from +4 to -2 so we add -6r(t-2). But we need to stop the waveform at t=3. Hence we have to make slope 0. Which can be done by adding +2r(t-3). Final equation is given as

2r(t)-6r(t-1.5)+8r(t-1.5)-6r(t-2)+2r(t-3)

Q15) Find IL(0)

Diagram

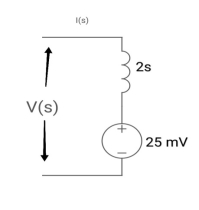
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_224139.jpg$

A15)

Comparing with ckf,

L = 2H

LiL (0) = 25 mv

IL (0) = 12.5 m A

Q16) Find voltage across capacitor?

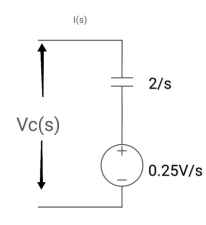
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_224353.jpg$

A16)

Comparing with circuit,

1/cs = 2/5

C=1/2f

Vc (0)/s = 0.25v/5

Vc(0)= .25v

Q17) Find Vc(0)?

Diagram

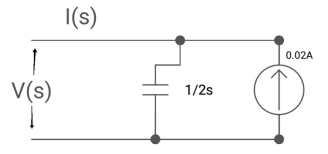
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_224735.jpg$

A17)

1/cs = 1/2S

C=2F

CVc (0) = 0.02

Vc(0)= 0.01

Sign Up