Unit – 3
Graph theory
Q1) Find total possible no. Of trees
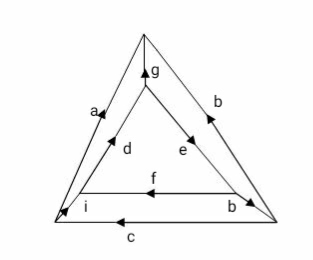
A1)
T = n (n-2)
n = no. Of nodes
T = 6 (6-2) = 6 4
Q2)
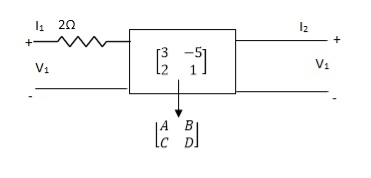
Find out overall transmission parameter?
A2)
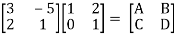
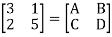
Q3)
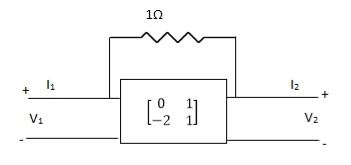
Find overall Y-parameter?
A3)
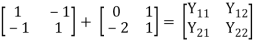
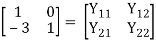
Q4)
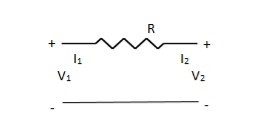
A4)
V1 – I1R – V2 = 0
V1 – V2 = I1R
I1 =  V1 -
V1 -  V2
V2
V2 = I2R + V1
I2 = -  V1 +
V1 +  V2
V2
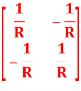
Y11 = 
Y12 = Y21 = 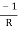
Y22 = 
Q5)
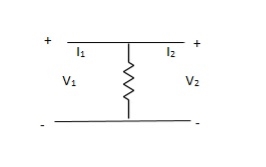
A5)
Y-parameter does not exist as V1 = V2
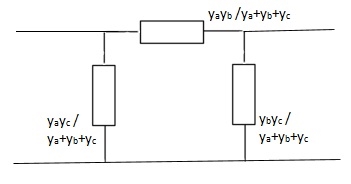
Q6)
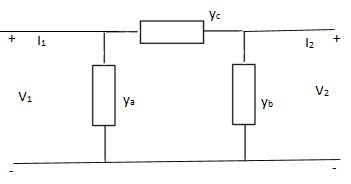
A6)
I1 = V1Ya + (V1 – V2)Yc
I1 = (Ya + Yc)V1 - YcV2
I2 = V2Yb + (V2 – V1)Yc
I1 = (Yb + Yc)V2 - YcV1
Y11 = Yb + Yc
Y12 = Y21 = - Yc
Y22 = Yb + Yc
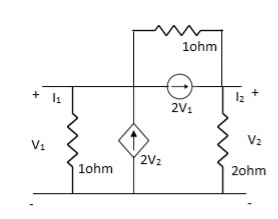
Q7)
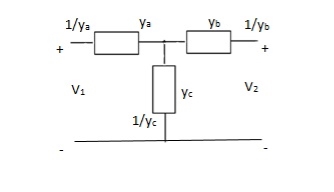
A7)
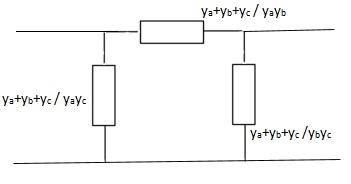
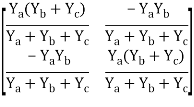
Q7)
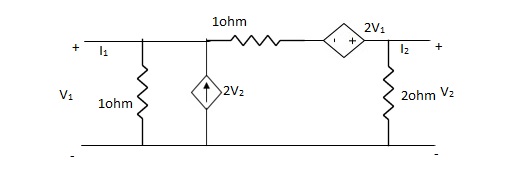
Find Y-parameter?
A8)
-I1 + 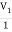 – 2V2 +
– 2V2 + 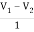 + 2V1 = 0
+ 2V1 = 0
I1= V1 + V1 - 3V2 + 2V1
I1= 4V1 - 3V2V
V2 + 2V2- 2V1 = 2(I2 + 2V1)
- 2V1 + 3V2 = 2(I2 + 2V1)
3V2 - 2V1 – 4V1 = 2I2
I2 = -3V1 +  V2
V2
Y11 = 4
Y12 = -3
Y21 = -3
Y22 = 
Q8)
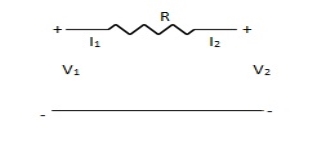
Find Z-parameter
A9)
I1 = -I2
Current dependent so Z-parameter doesn’t exist
Q9)
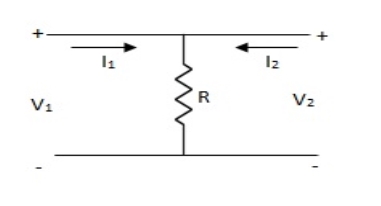
Find z-parameter
A10)
V1 =R (I1 + I2)
V2 = R (I1 + I2)
Z11 = Z12 = Z21 = Z22 = R
Q10)
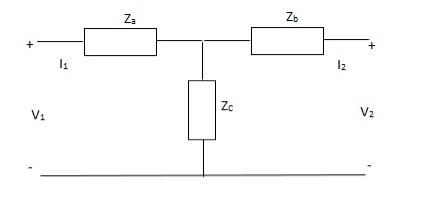
A11)
V1 = I1Za + I1Zc + I2Zc
= (Za + Zc)I1 + ZcI2
V2 = I2Zb + I2Zc + I1Zc
= (Zb + Zc)I1 + ZcI1
Z11 = (Za + Zc)
Z12 = Zc = Z21
Z22 = (Zb + Zc)
Q11)
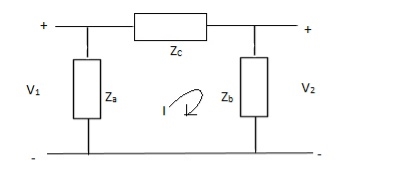
A12)
V1 = Za(I1 - I)
(I - I1)Za+ IZc+ Zb(I + I2) = 0
I(Za + Zb + Zc) – I1Za + I2Zb = 0
I = 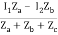
V1 = ZaI1 - Za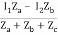
= 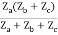 I1 + I2
I1 + I2 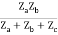
V2 = Zb(I2 + I)
= ZbI2 + Zb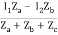
= 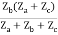 I2 + I2
I2 + I2 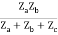
Z11 = 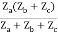
Z12 = Z21 = 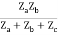
Z22 = 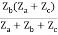
Can be solved by Y-A conversion
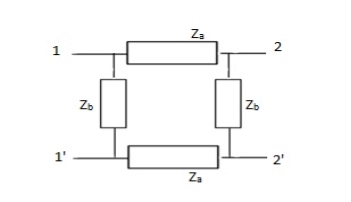
Q12)
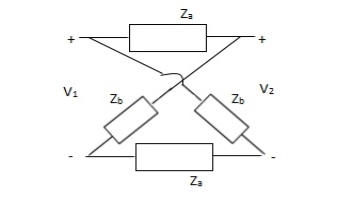
A13)
Z11 = 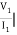 I2=0
I2=0
V1 -  (Za + Zb) = 0
(Za + Zb) = 0
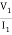 = Z11 =
= Z11 = 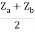
Z21 = 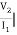 I2=0
I2=0
V2 -  Zb +
Zb + Za = 0
Za = 0
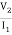 =
= 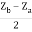
Z12 = 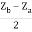
Z22 = 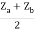
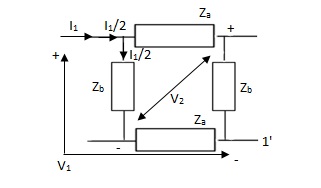
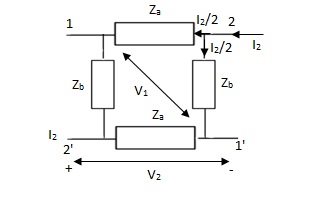
Q13)
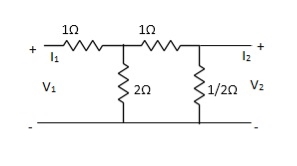
Find Z21 ?
A14)
Z21 = 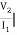 I2=0
I2=0
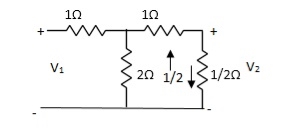
I1/2 = 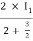
=  I1
I1
V2 =  I1/2
I1/2
=  ×
×  I1
I1
=  I1
I1
Z21 = 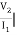 I2 = 0 =
I2 = 0 =  I1 Ω
I1 Ω
Q14)
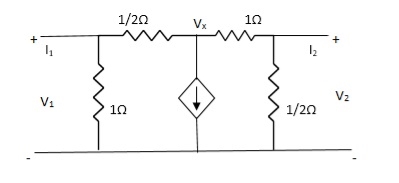
A15)
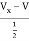 +
+ 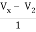 + 2V1 = 0
+ 2V1 = 0
2Vx – 2V1 + Vx – V2 + 2V1 = 0
3Vx = V2
Vx = 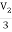
I1 = V1 + 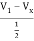
= 3V1 – 2Vx
= 3V1 – 2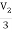
V1 = 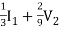
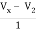 + 2V2 = I2
+ 2V2 = I2
3V2 - 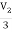 = I2
= I2
 V2 = I2
V2 = I2
V2 =  I2
I2
V1 = 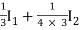
= 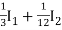
Z11 = 
Z12 = 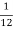
Z21 = 0
Z22 = 