Unit – 4
Network functions
Q1) For the network shown below 1)show that with port 2)open the driving point input impedance 1π)b)find the voltage , ratio transfer function 1/2 for the two port network.
A1)
From above network we take L.T
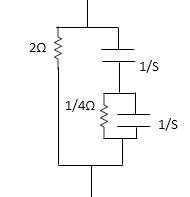
Reducing 4 we gel,
Z1=(25+25*1 / 25+1)*1
25+25*1 / 25+1*1
Z1=4S2+45/452+65+1
Z2=
Z2=(1/4S/1/4+1/5+1/5)*2
1/45/1/4+1/3+1/5+2
=2(5+5+4) / 5+5+4+25(5+4) = 2(25+4)/252+10S+4
Z2=25+4/252+10+4
Applying KVL, in the circuit
V1=I1Z1+I,Z2 -----------1
V2= I1Z2 ...............2
.: V1=I1Z1+V
V1 / I1= (Z1+Z2) (from----1)
Dividing equation 2 by 1
G12=Z 2 / Z1+Z2
Calculating z11 we have,
Z11=Z1+Z2
Z11 = 4S2+4S / 4S2+6S+1 * 2S+4/S2+SS+2
=(4S2+4S)(S2+SS+2)+(2S+4)(4S2+6S+1) / (4S2+6S+1)(S2+SS+2)
Z11=4S4+20S3+8S2+4S3+20S2+8S+8S3+12S2+25+16S2+4 /(4S2+6S+1)(S2+SS+2)
= (4S4+32S3+5652+345+4 / (4S2+6S+1)(S2+SS+2)
G12= Z2 / Z1+Z2
= (2S+4) / (S2+SS+2) / (4S+32S3+56S2+34S+4) / (4S2+6S+1)(S2+SS+)
G12= (2S+4)(4S2+6S+1) / 4S4+32S3+56S2+34S+4
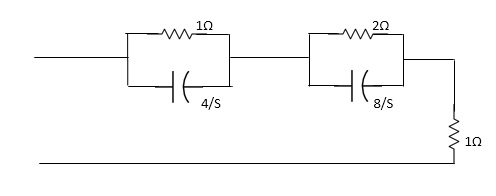
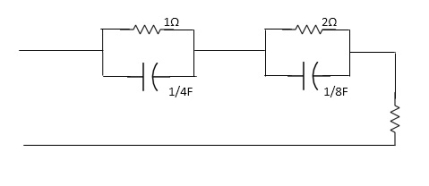Q2) For the network shown, find driving point input impedance .plot the pole zero pattern for each as well.
A2)
For fig 1) taking L.T we have
Z11= 1+ 1 /S/3+1/25+1/1/4S
=1+ 1/ 5/3+1/6S
=1+ 18S/6S2+3
Z11=6S2+3+18S/ 6S2+3 =2S2+6S+2/2S2+1
Zeros of equations are taking lt.of circuit b)
Z11= 1*4/5
1+4/5+2.8/3/2+8/5+1
=4/5+4 + 16/ 25+8+1
= 4/5+4+8/5+4+1
=s+12+4/(5+4)
Z11= S+16/(S+4)
For zeros of system
s+16=0
s=-16
For poles of system
s+4=0
s=-4
Q2) Find whether the following network function represent the driving point function.
a) f(s)= (s+1)/(s2+1) b) f(s) = 3s2+2s+1/ss3+9s2+3s+2 c) f(s)=(s2+1)2/s2(s+3)
A3)
a) f(s)=s+1/s2+1
It represents the driving point function:
b) F(S)= 3S2+2S+1 / 5S3+9S2+3S+2
It represents the driving point function.
b)F(s)=3s2+2s+1/5s3+9s2+3s+2
It represents the driving point function
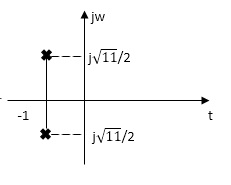
c) f(s) = (s2+1)2/s2(5+3)
It has representative zeros, hence not valid
( s2+1)2=0
s2=+-1
s2=+-j,+-j
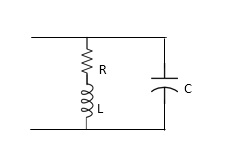
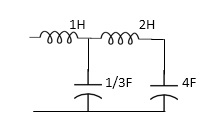
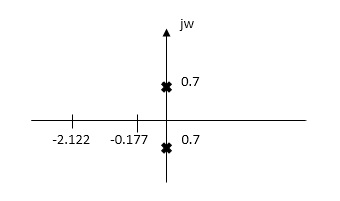
Q4) For network below 1), pole - zero pattern is represented in fig 2) , find numerical value of R,L and c for z (0)=1?
Diagram=
A4)
Calculating z(s) by taking L.T of fig 1)
z(s) = (R+SL)*1/CS
(R+SL)+1/CS = R+SL / SRC+S2LC+1
Z(S)= S+R/L / C [S2+R/L S+1/LC]
Given z(0)=1
z(0)=R/L / C/LC =1
Z(0)=R=1
.: R=1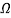
Polls are given as
S2+RS/L+1/LC=0
S=-R/2L +J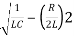
Zeros are given as
S+R / L=0
From pole zero plot value of pole location is at -1 so
-R / L = -1
-1/ L=-1
L=1H
Also imaginary part of pole from plot is
=
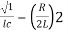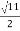
1/LC-(R/2L)2 =11/4
1/C-(1/2)2=11/4
1/C-1/4=11/4
1/C=11/4+1/4
1/C=12/4 =3
C=1/3 F
Hence, value of R=1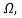
L=14 and c=1/3 f
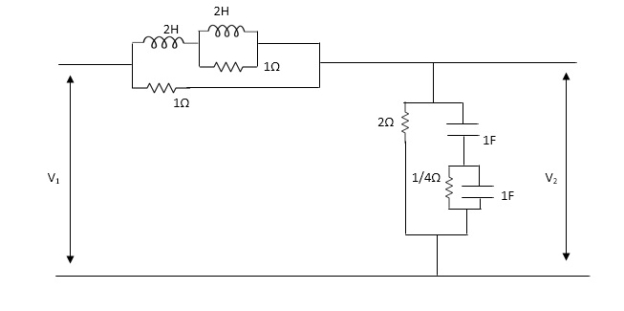
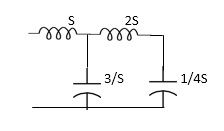
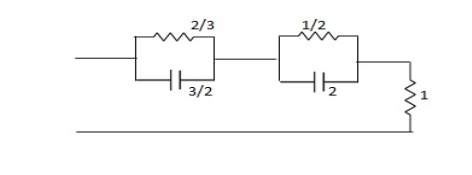
Q3) FOR the following circuits ,FIND G12(S) =v2/v1
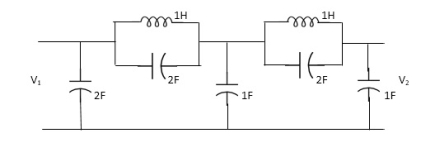
A5)
Taking Laplace transform of above we have
Applying KCL at node v0
V0-V1(S) / S*1/2S/(S+1/2S) +V0+V2(S)/ (S*1/2S)/(S+1/2S)+V0/1/S=0
For Porr 2)We have ,
v2-v0/(s*1/2s)/(s+1/2s)+v2/1/s =0 ---------(ii)
(v2-v0)(2s2+1) / s +sv2=0
v2 [2s2+1/s+s] = v0( 2s2+1)/ s
v0=v2(3s2+1) / (2s2+1)-----------(iii)
From (i) we have ,
(v0-v1) /s (2s2+1) *sv0+(v0-v2)/5 (s2+1) =0
(2s2+1/5)v0-(2s2+1)/sv1+sv0+(2s2+1)/sv0-(s2+1)/s v2=0
(2s2+1)v1=(5s2+2)v0-(2s2+1)v2
Substitute value v0 from (iii) above
(2s2+1)v1 =[( 5s2+2)(3s2+1) /(2s2+1)-(2s2+1)]v2
(2s2+1)v1=(15s4+5s2+6s2+2-4s4+4s2) / (2s2+1 *v2
G12(s) = v2/v1 = (2s2+1) 2/11s4+15s2+1
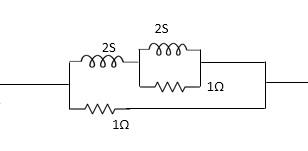
Q4) Find the transfer function admittance ratio
Y12(s) = I2(S) / V1(S)
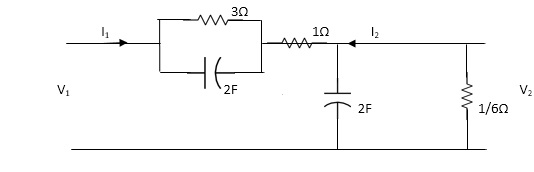
A6)
Taking Laplace transform of above figure
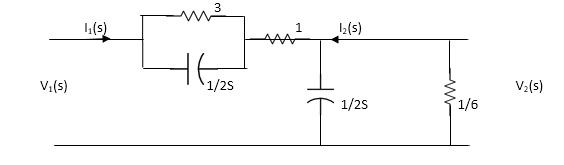
Applying KCL we get,
(V2-V1) / (3*1/2S) / (3+1/2S) * V2/ 1/2S+ V2/1/6 =0
(Y2-V1)(6S+1) / (6S+4) * (2S+6)V2V=0
BUT I2=-6V2
V2=-I2/6
We have ,
(6s+1) / (6s+4)*v2-(6s+1) / (6s+4)*v1 +(2s+6)v2=0
-[6s+1 / 6s+s+2s+6]I2 / 6 =V1(6S+1) / 6S+4
-[6S+1(2S+6)(6S+4)]I2= 6(6S+1)V1
-[(6S+1)*12S2+36S+8S+24] I2=6(6S+1)
I2 / V1 =-6(6S+1) / 12S2+50S+25
Y12(S) = I2(S) / V1(S) = -6(6S+1) / 12S2+50S+25
Q5) For the given polynomials find whether they are Hurwitz polynomials or not.
a). F1(s) = s+ 3
b). F2(s) = s2 + 5
c). F3(s) = s2 + 5s + 6
d). F4(s) = s3 + 4s2 + 8s + 4
A7)
a). F1(s) = s + 3
s = -3
Its Hurwitz polynomial
b). F2(s) = s2 + 5
s = Ij√5
Its Hurwitz polynomial
c). F3(s) = s2 + 5s + 6
s2 + 5s + 6
s2 + 2s + 3s + 2 x 3
(s + 3)(s + 2)
F3(s) =>s = -3, -2
It is Hurwitz polynomial.
d). F4(s) = s3 + 4s2 + 8s + 4
E(s) = 4s2 + 4O(s) = s3 + 8s
4(s2 + 1 )s(s2 + 8)
s = 1js = 1j2√2
Its Hurwitz polynomial
Q6). Find the range of K for which the polynomial 2s4 + s3 + ks2 + s+ 2 is Hurwitz?
A8)
s3 + s + 2 ) 2s4 + ks2 + 2 ( 2s
2s4 + 2s2
(k-2)s2 + 2 ) s3 + s + 2 (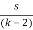
s3 +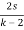 
------------------
s(1 –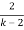 
) + 2 ) (k-2)s2+ 2 (
------------------
k-2 > 0 (1 –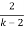 
> 0
k > 2
1 >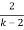
k-2 > 2
k > 4
k > 2, k > 4
k > 4
Q7) Find whether the given function F(s) = s + 4 / s2 + 2s + sis positive real or not?
A9)
By inspection check the function
(ii) Numerator and Denominator should both be Hurwitz
(iii) Real part of function must be positive for all values of W.
N(s) = s+ 4D(s) = s2 + 2s + s
It is HurwitzIt is Hurwitz
Finding real part of function, s= jw.
F(jw) =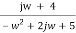 
= 
+
= 
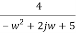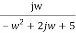
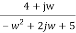x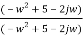 
= 
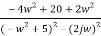
Real part
= 
= 
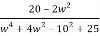
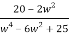
For, w1 = 1, 2, …
For w > 3 function becomes negative. So not positive real.
Q8) .8s6 + 4s5 + 34s4 + 16s3 + 32s2 + 12s + 6. Find whether this is Hurwitz or not?
A10)
4s5 + 16s3 + 12s ) 8s6 + 34s4 + 32s2 + 6 ( 2s
8s6 + 32s4 + 24s2
---------------------------
2s4 + 8s2 + 6 ) 4s5 + 16s3 + 12s ( 2s
4s5 + 16s3 + 12s
-----------------------
* * *
This is the case of premature termination.
F(s) = F1(s).F2(s)
From above F1(s) = 2s4 + 8s2+ 6
F2(s) = 8s6 + 4s5 + 34s4 + 16s3 + 32s2 + 12s + 6
--------------------------------------------------------
2s4 + 8s2 + 6
2s4 + 8s2 + 6 ) 8s6 + 4s5 + 34s4 + 16s3 + 32s2 + 12s + 6 ( 4s2 + 2s + 1
8s6 + 32s4 + 24s2
---------------------------------------------------------
4s5 + 16s3 + 8s2 + 12s + 6 + 2s4
4s5 + 16s3 + 12s + 2s4
-------------------------------------------------
2s4 + 8s2 + 6
2s4 + 8s2 + 6
----------------------
* *
F1(s) = 2s4 + 8s2+ 6 – It is Hurwitz
F2(s) = 4s2 + 2s+ 1 – Has one root or RHS
F(s) is not Hurwitz as F2(s) is non Hurwitz.
Q9) For the function Z(s) = s2 + 6s + 8 / s2 + 4s+ 3 is RL or RC.
Realise the above function.
A11)
Z(s) =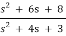
= 
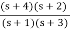
All roots are -4, -2, (-1)->lowest, -3
Since lowest root is pole so its RC.
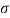1 = 1, 
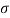2= 3
Z(s) =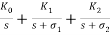 
K0 =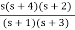 
|S->0 = 0
K∞ =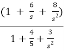 
S->∞
K∞ = 1 => R∞ =1
K1 = 3/2 => R1 = 2/3 => C1 = 2/3
K2 =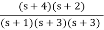 
|S = -3
K2 = 1 / 2 => C2 = 2, R2 = 1/2
Q10) Realise using foster form (2), Y(s) = s2 + 6s + 8 / s2 + 4s+ 3
A12)
Above function is RL admittance as lowest frequency is pole.
Y(S) =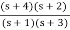 
K0 =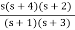 
|s->0 = 0 , L0 = ∞
K1 =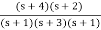 
|s = -1
K1 = 3 / 2
L1 = 2 / 3, R1 = 2 / 3 (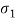
/ K1)
K2 = (s+4)(s+2) / (s+1)(s+3)(s+3) |S = -3
= 1 / 2, L2 = 2, R2 =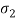 
/ K2 = 3 / ½ = 6
K∞= (s+4)(s+2) / (s+1)(s+3)|s -> ∞
= (1 + 4 / s)(1 + 2 / s) / (1 + 1 / s)(1 + 3 / s )|S -> ∞
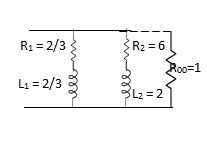K∞ = 1, R∞ = 1 / K∞ = 1
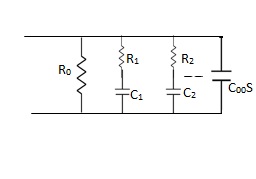
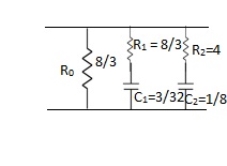
Q11) Realise the following function Y(s) = s2 + 4s + 3 / s2 + 6s+ 8
A13)
Lowest critical frequency is zero.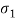 
= +4, 
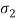= +2
Y(s) =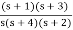
K0 = 3 / 8, R0 = 8 / 3
K∞ =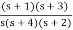 
|S->∞
= 
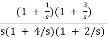/ S->∞
K∞ = 0, C∞ = 0
K1 =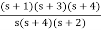 
|S = -4
K1 = 3/8, R1 = 8/3
C1 = K1/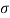
1 = 3/8 x ¼ = 3/32
K2 = (s+1)(s+3) / s(s+4)(s+2)|S = -2 = 1/4
K2 = 1/4, R2 = 4
C2 = K2/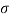 
2 = 1/8
