UNIT-1
BASICS OF SEMICONDUCTOR PHYSICS
Q1) For an intrinsic Semiconductor with a band gap of 0.7 eV, determine the position of EF at T = 300 K if m*h = 6m*e
A1)
 |
Q2) Derive expression for carrier concentration for intrinsic semiconductors? Explain Fermi level for Intrinsic semiconductors and what is the effect of temperature on Fermi level?
A2)
Intrinsic semiconductors—carrier concentration
Here we will calculate the number of electrons excited into conduction band at temperature T and also the hole concentration in the valence band. It is assumed that the electrons in the conduction band behave as if they are free particles with effective mass me* and the holes near the top of the valence band behave as if they are free particles with effective mass mh*.
Here we will calculate the electron concentration, hole concentration
Density of Electrons in Conduction Band
The number of free electrons per unit volume of semiconductor having energies in between E and E + dE is represented as N(E) dE
dE = width of Energy band
Therefore, we have:
N(E) dE = ge(E) dE fe(E) ……….(1)
ge(E) = The density of electron states per unit volume
fe(E) = Fermi-Dirac distribution function i.e. probability that an electron occupies an electron state
The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating N(E) dE between the limits Ec and Ect
Where Ec = the bottom energy levels of conduction band
Ect = the bottom and top energy levels of conduction band
n = 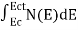 ……….(2)
……….(2)
Can be written as
n = 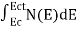 =
= 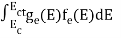
n = 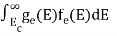 -
- 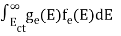 ……….(3)
……….(3)
We know that above Ect, there is no electrons.
Hence, Equation (3) becomes
n = 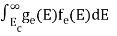 -
- 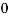
n =  ……….(4)
……….(4)
The Fermi-Dirac distribution function fe(E) can be represented as:
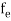 (E) =
(E) =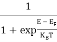 ……….(5)
……….(5)
Compared to the exponential value, so the ‘1’ in the denominator can be neglected.
So 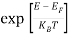 >>1
>>1
Hence, 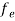 (E) =
(E) =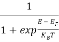 =
= 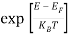 ……….(6)
……….(6)
The density of electron states ge(E) in the energy space from E = 0 to E can be written as:
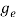 (E) =
(E) =  [
[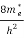 ]3/2 (E - 0) ½ ……….(7)
]3/2 (E - 0) ½ ……….(7)
Where me* is the effective mass of an electron and h is Planck’s constant.
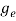 (E)dE =
(E)dE =  [
[ ]3/2 (E - 0) ½dE ……….(8)
]3/2 (E - 0) ½dE ……….(8)
To evaluate n, the density of states is counted from Ec, since the minimum energy state in conduction band is Ec. So eq (8) can become
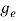 (E)dE =
(E)dE =  [
[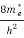 ]3/2 (E - Ec) ½dE ……….(9)
]3/2 (E - Ec) ½dE ……….(9)
Substituting Equations (6) and (9) in (4) gives
n = 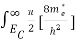 3/2
3/2 (E-
(E-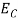 )1/2
)1/2 dE
dE
n = [
[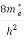 ]3/2
]3/2 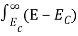 1/2
1/2 dE………… (10)
dE………… (10)
The above equation can be simplified by the following substitution:
Put ɛ = E − Ec ………… (11)
So, dɛ = dE
In Equation (11), Ec is constant, as we change the variable E to ε in Equation (10), the integral limits also change.
In Equation (11), as E → Ec then ε → 0 and E → ∞, then ε also → ∞.
The exponential term in Equation (10) becomes:
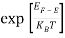 = exp [
= exp [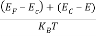 ] = exp [
] = exp [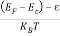 ]
]
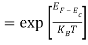
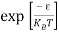 ………… (12)
………… (12)
Substituting Equations (11) and (12) in (10), we get:
n = [
[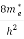 ]3/2
]3/2  dE
dE
n = [
[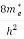 ]3/2
]3/2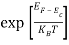
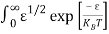 dE………… (13)
dE………… (13)
Above integral (I) can be simplified by substitution. Put ε = x2
So that dɛ = 2x dx
I =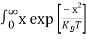 2x dx
2x dx
=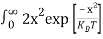 dx
dx
= =
=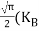 T)3/2………… (14)
T)3/2………… (14)
Substituting Equation (14) in (13) gives:
n = [
[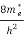 ]3/2
]3/2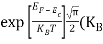 T)3/2
T)3/2
n =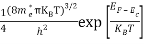
n = 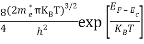
n = 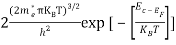 ………… (15)
………… (15)
The term 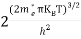 is almost a constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol Nc. So, we have
is almost a constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol Nc. So, we have
n =Nc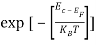 ………… (16)
………… (16)
Density of Holes in Valence Band
The number of holes per unit volume of semiconductor in the energy range E and E + dE in valence band is represented as P(E) dE. Proceeding same way(as in case of electrons) we have
Therefore, we have:
P(E) dE = gh(E) dE fh(E) ……….(17)
dE = width of Energy band
gh(E) = The density of holes states per unit volume
fh(E) = Fermi-Dirac distribution function i.e. probability that an hole occupies an electron state
The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating P(E) dE between the limits Evb and EV
Where EV = the bottom energy levels of valence band
Evb = the bottom and top energy levels of valence band
The total number of holes present in the valence band per unit volume of material ‘p’ is obtained by integrating P(E) dE
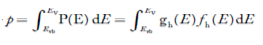 ……….(18)
……….(18)
Equation (18) can be represented as:
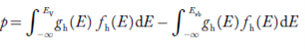 ……….(19)
……….(19)
Now we know that below Evb no holes is present. Hence, Equation (19) becomes
 ……….(20)
……….(20)
We know hole can also be defined as absence of an electron.
Presence of a hole = the absence of an electron
Hence, the Fermi-Dirac function of holes fh(E) in the valence band is:
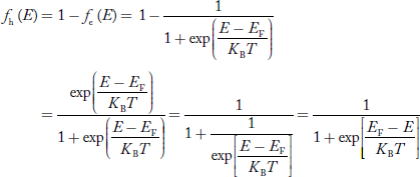
Compared to exponential, the ‘1’ in the denominator is negligible,
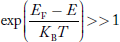
Hence,
 ……….(21)
……….(21)
The density of hole states between E and E + dE in valence band can be written similar to Equation (8.9) for electrons.
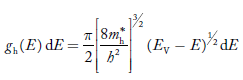 ……….(22)
……….(22)
Where mh* is the effective mass of hole.
Substituting Equations (21) and (22) in (20),
 ……….(23)
……….(23)
The above equation can be simplified by the substitution:
Put ɛ = EV − E ............. (24)
So dɛ = − dE
In Equation (24), EV is constant, as we change the variable E to ε in Equation (23), the integral limits also change.
In Equation (24),
As E → EV then ε → 0
And E→ −∞, then ε → ∞
The exponential term in Equation (23) becomes:
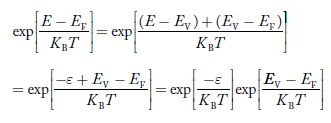 ............. (25)
............. (25)
Substituting Equations (24) and (25) in (23), we get:
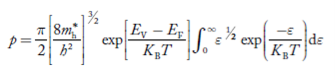 ………….(26)
………….(26)
From Equation (14), we know the integral value 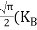 T)3/2 put here and we get
T)3/2 put here and we get
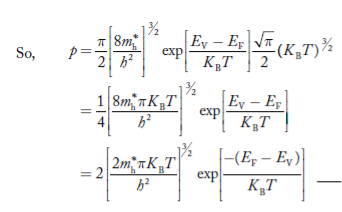 ………….(27)
………….(27)
….The term 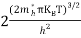 is almost constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol NV. So, we have
is almost constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol NV. So, we have
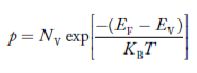 …………… (28)
…………… (28)
Q3) Explain Fermi level for Intrinsic semiconductors and what is the effect of temperature on Fermi level?
A3)
Fermi Level
We know that in intrinsic semiconductor
Electron concentration ‘n’ = Hole concentration ‘p’
Equating Equations (15) and (27), we get
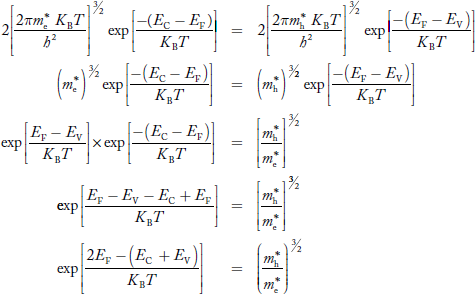 Taking logarithms on both sides, we get 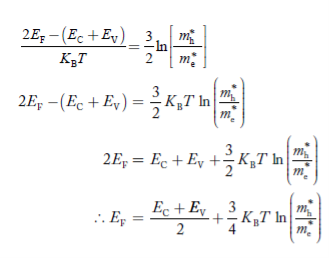 |
Normally, mh* is greater than me*, since ln 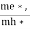 is very small so that EF is just lie in the middle of energy gap
is very small so that EF is just lie in the middle of energy gap
Temperature effect on Fermi level
Fermi level slightly rises with increase of temperature.
But in case of pure intrinsic semiconductor like Si and Ge,
mh* ≈ me*
So in these cases Fermi level lies at the middle of energy gap.
Q4) Calculate the intrinsic concentration of charge carriers at 300 K given that m *e =0.12m o ,m *h =0.28mo and the value of brand gap = 0.67 eV.
A4)
 |
Q5) Where Fermi level lie in case of p type and n type extrinsic semiconductor? Or Derive expression for Carrier Concentration in Extrinsic Semiconductors.
A5)
Carrier Concentration in Extrinsic Semiconductors
The number of charge carriers present per unit volume of a semiconductor material is called carrier concentration.
Suppose donor and acceptor atoms are doped in a semiconductor.
At temperature T K,
n = number of conduction electrons
p = number of holes
N−A = number of acceptor ions
N+D = number of donor ions
We know that the below equation hold good in semiconductor. The total negative charge due to conduction electrons and acceptor ions is equal to holes and donor ions in unit volume of material.
So the material will be considered neutral if,
n + N−A = p + N+D ………. (34)
Equation (34) is called charge neutrality equation.
In the above equation
 ……….. (35)
……….. (35)
Concentration of acceptor ions N−A = acceptor concentration x probability of finding an electron in acceptor level
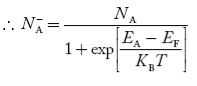 ………..(36)
………..(36)
Similarly, the donor ions concentration is
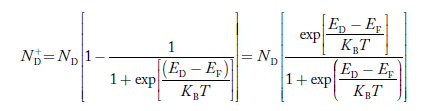
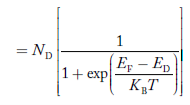 ………..(37)
………..(37)
In n-type material
Note nn represents electrons in n-type material
pn represents holes concentration in n-type material.
There are no acceptor atoms so N−A = 0.
At 0 K, all the electron states in donor level are occupied by electrons.
As the temperature is increased from 0 K, some of the electrons jump from these donor states into the conduction band.
Also the concentration of holes is extremely less compared with the concentration of conduction electrons [p << n]
From Equation (34) we have
n = p N+D
(Or) n ≈ N+D …………(38) [since p << N+D]
At temperature T K,
As the temperature increase Almost all the donor atoms donate electrons to conduction band.
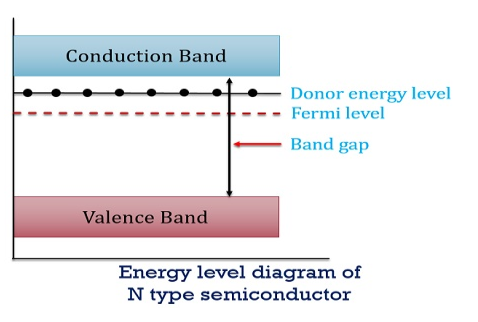 |
So, in n-type material, the free electron concentration is almost equal to the donor atoms.
So we can rewrite the above equation as
nn ≈ ND …………….(39)
Where nn represents electrons in n-type material
Also the hole concentration in n-type material can be obtained by applying law of mass action nn pn =ni2
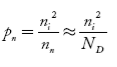 …………..(40)
…………..(40)
Where pn represents holes concentration in n-type material.
In n-type material at 0 K, the Fermi energy level lies in the middle of Ec and ED
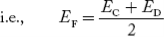
At temperature> 0K
 ……….(41)
……….(41)
With increase in temperature the Fermi level shifts upwards according to Equation (61) slightly due to ionization of donor atoms.
With further increase of temperature, electron-hole pairs are generated due to the breaking of covalent bonds, hence Fermi level shifts downwards.
In p-type semiconductor
Note
pp represents holes in p-type material
np represents electrons in p-type material
There are no donor atoms so means no ions present  = 0.
= 0.
At 0 K, all the acceptor levels are not occupied by electrons.
As the temperature is increased from 0 K, some electrons jump from top valence band energy levels to the acceptor states, leaving holes in the valence band and acceptor ions  are formed.
are formed.
At some room temperature T K, concentration of conduction electrons is extremely less compared with hole concentration.
∴ From Equation (34), we have
n + N−A = p ……………(42)
(or) N−A ≈ p ……………. (43) [since n << N−A]
At temperature T K, in p-type material,
The hole concentration is almost equal to the acceptor atoms in unit volume of the material.
So, Equation (43) can be written as
pp ≈ NA……………….(44)
Where pp represents holes in p-type material
The electron concentration in p-type material can be obtained by applying law of mass action as nppp = ni2
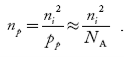 …………….(45)
…………….(45)
Where np represents free electron concentration in p-type material.
 |
In p-type material, the Fermi level lies in between EV and EA at 0 K

As the temperature is increased from 0 K, the Fermi level shifts downwards slightly as per Equation (46) due to ionization of acceptor atoms.
And with further increase of temperature, electron-hole pairs are generated due to the breaking of covalent bonds, so Fermi level shifts upwards.
Q6) What is Recombination in semiconductor? Discuss any two different processes which lead to recombination?
A6)
RECOMBINATION-GENERATION
Carrier generation is a process where electron-hole pairs are created by exciting an electron from the valence band of the semiconductor to the conduction band, thereby creating a hole in the valence band.
Recombination is the reverse process where electrons from the conduction and holes from valence band recombine and are annihilated.
These processes must conserve both quantized energy and momentum, and the vibrating lattice plays a large role in conserving momentum.
- Recombination and generation are always happening in semiconductors both optically and thermally.
- Their rates are in balance at equilibrium.
- If the product of the rate becomes greater than the recombination rate, again driving the system back towards equilibrium.
- As the electron and hole densities is a constant at equilibrium, maintained by recombination and generation occurring at equal rates.
- When there is a surplus of carriers the rate of recombination becomes greater than the rate of generation, driving the system back towards equilibrium.
In semiconductors several different processes exist which lead to recombination, the most important ones are:
1) Band-to-band recombination
2) R-G centres,
3) Auger and impact ionization.
Band-to-band recombination or Radiative recombination is the reverse process of photon absorption, where an electron drops back down to its equilibrium energy band and radiates a photon.
It is the process of electrons jumping down from the conduction band to the valence band in a radiative manner.
During band-to-band recombination the energy absorbed by a material is released in the form of photons. Generally, these released photons contain the same or less energy than those initially absorbed.
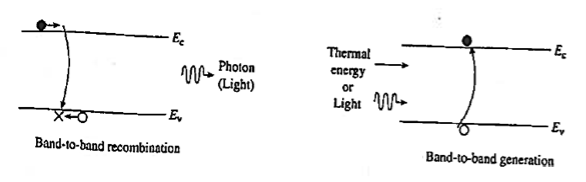 |
Figure 18: Band-to-band recombination
The photon emitted may have the energy of the band gap difference or less, depending on how much energy is lost in the mechanism
Radiative recombination plays a more major role in direct band semiconductors.
The total radiative recombination rate, given below as R, is proportional to the product of the concentration of occupied states (electrons, n) in the conduction band and that of the unoccupied states in the valence band (holes, p)
R= Bnp
Band-to-band recombination depends on the density of available electrons and holes. Both carrier types need to be available in the recombination process. Therefore, the rate is expected to be proportional to the product of n and p. Also, in thermal equilibrium, the recombination rate must equal the generation rate since there is no net recombination or generation. As the product of n and p equals ni2 in thermal equilibrium, the net recombination rate can be expressed as:
U= B(np-ni2)
Where B is the bimolecular recombination constant for a given semiconductor. It can be calculated from the semiconductor’s absorption coefficient. ni2 is the familiar “intrinsic carrier concentration”
R—G CENTER
Recombination involves a "third party," or intermediary, and takes place only at special locations within the semiconductor known as R—G centers.
Recombination at an R—G center is a two-step process. First, one type of carrier, say an electron, strays into the vicinity of an R—G center, is caught by the potential well associated with the center, loses energy, and is trapped. Subsequently, a hole conies along, is attracted to the trapped electron, loses energy, and annihilates the electron within the center. Alternatively, one can think of the electron as losing energy a second time and annihilating the hole in the valence band. R—G center recombination, also called indirect recombination, typically releases thermal energy (heat) during the process or, equivalently, produces lattice vibrations.
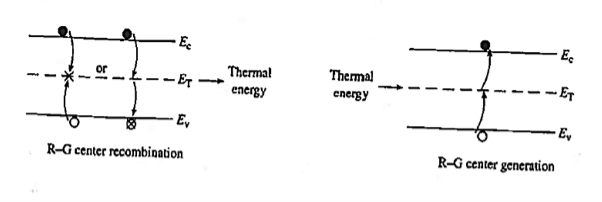 |
Figure 19: R—G Center
R—G centers are lattice defects or special impurity atoms such as gold in Si. Lattice defects and the special atoms in the form of unintentional impurities are present even in semiconductors of the highest available purity. The R—G center concentration, however, is normally very low compared to the acceptor and donor concentrations in device-quality materials. The most important property of the R—G centers is the introduction of allowed electronic levels near the center of the band gap. These levels are identified by the ET energy label in Figure 19. The near mid-gap positioning of the levels is all-important because it distinguishes R-G centers from donors and acceptors. The mid-gap levels introduced by select R—G center impurities in Si are summarized in Figure 20.
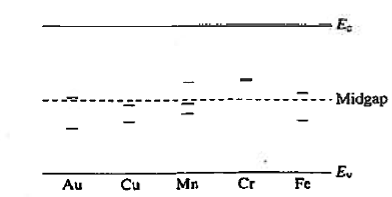 |
Figure 20: mid-gap levels introduced by select R—G center impurities in Si
Q7) Explain auger recombination and impact ionization?
A7)
Another non-radiative recombination is Auger recombination, it is given off in the form of kinetic energy to another electron. The energy that becomes available through electron-hole recombination (Eg) is dissipated by the excitation of a free electron high into the conduction band, or by a hole deeply excited into the valence band. The highly excited carrier will subsequently lose energy by multiple phonon emission until they are close to the band edge. Recombination rate due to the Auger process
RAuger = Cpnp2(22)
RAuger = Cnn2p(23)
Auger recombination reduces the luminescence efficiency in semiconductors only at very high excitation intensity or at very high carrier injection currents. At lower carrier concentrations, the Auger recombination rate is very small and can be neglected.
Auger recombination involves three particles: an electron and holes, which recombine in a band-to-band transition and give off the resulting energy to another electron or hole. The expression for the net recombination rate is therefore similar to that of band-to-band recombination but includes the density of the electrons or holes, which receive the released energy from the electron-hole annihilation.
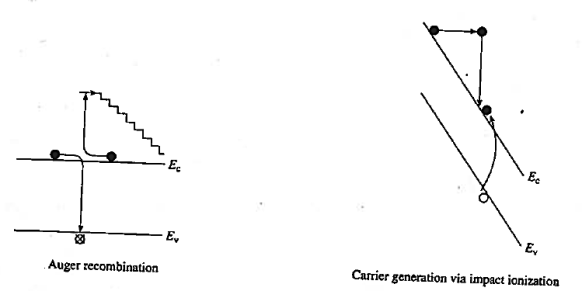 |
Figure 21: Auger recombination and Impact ionization
As shown in figure Auger Recombination is band-to-band recombination occurs simultaneously with the collision between two like carriers. The energy released by the recombination is transferred during the collision to the surviving carrier. This highly energetic carrier subsequently "thermalizes" —loses energy in small steps through heat-producing collisions with the semiconductor lattice. The "staircase" in Figure represents the envisioned stepwise loss of energy.
In other words Auger recombination, the energy is given to a third carrier which is excited to a higher energy level without moving to another energy band.
After the interaction, the third carrier normally loses its excess energy to thermal vibrations. Since this process is a three-particle interaction, it is normally only significant in non-equilibrium conditions when the carrier density is very high.
Auger recombination is most important at high carrier concentrations caused by heavy doping. In silicon-based solar cells, Auger recombination limits the lifetime and ultimate efficiency.
The more heavily doped the material is, the shorter the Auger recombination lifetime.
Impact ionization
Impact ionization, the inverse of Auger recombination, is visualized in Figure 21. In this process an electron–hole pair is produced as a result of energy released when a highly energetic carrier collides with the crystal lattice. The generation of carriers through impact ionization routinely occurs in the high -field regions of devices. We will see this process when treating breakdown in pn junctions.
Q8) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.
A8)
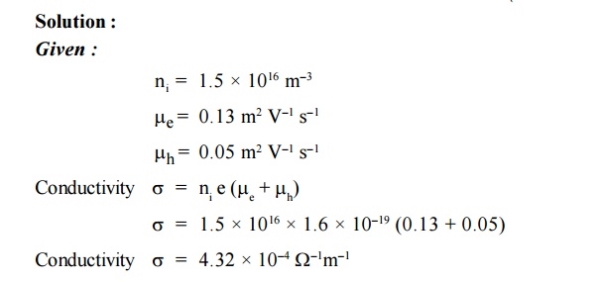 |
Q9) What is Drift current and diffusion currents? Derive expression for total hole and total electron current?
A9)
In case of semiconductors, we observe two kinds of currents.
- Drift current
- Diffusion current
Drift current Definition: - The flow of electric current due to the motion of charge carriers under the influence of external electric field is called drift current.
When an electric field E is applied across a semiconductor material, the charge carriers attain a drift velocity vd
So drift velocity vd =μ .E
The relation between current density J and drift velocity vd is
J = Nqvd
Where N is the carrier concentration
q is the charge of electron or hole
From equations (1) and (2), we get
Jdrift = Nq μE
μ is the mobility of charge carrier.
The above equation shows the general expression for drift current density. Drift current density due to electrons is
Je(drift) = neμeE
Where n is the electrons carrier concentration
And μe is the mobility of electrons.
Drift current density due to holes is
Jh(drift) = peμhE
Where p is the carrier concentration of holes.
μh is the mobility of holes
So Total drift current density
Jdrift (total) = Je(drift) + Jh(drift) = neμeE + peμhE
= eE (nμe+pμh )
Diffusion current
Definition:-The flow of electric current due to the motion of charge carriers under concentration gradient is called diffusion current
Or
The motion of charge carriers from the region of higher concentration to lower concentration leads to a current called diffusion current.
Let ∆N be the excess electron concentration. Then according to Fick’s law, the rate of diffusion of charge carriers is proportional to concentration gradient
Rate of diffusion of charge ∝ -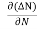
= - D
Where D is the diffusion coefficient of charge carriers.
The negative sign indicates decrease of N with increase of x So,
The diffusion current density Jdiffu is
Jdiffu = - qD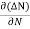
Where q is the charge of the charge carrier
Diffusion current density due to holes is
Jdiffu (hole) = - eDh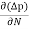
Diffusion current density due to electrons is (as electron carry negative charge so we will get +sign here.
Jdiffu (electrons) = eDe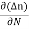
Jdiffu (total) = Jdiffu (hole) + Jdiffu (electrons)
Jdiffu (total) = - eDh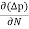 + eDe
+ eDe
The expression for total current density due to holes is
Jh (total) = Jh(drift) + Jdiffu (hole) = peμhE - eDh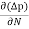
The expression for total current density due to electrons is
Je (total) = Je(drift) + Jdiffu (electrons) = neμeE + eDe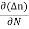
Q10) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.
A10)
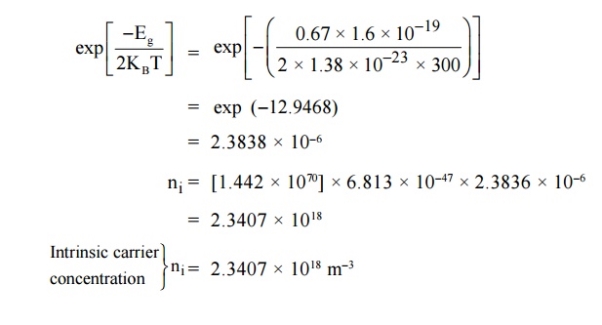 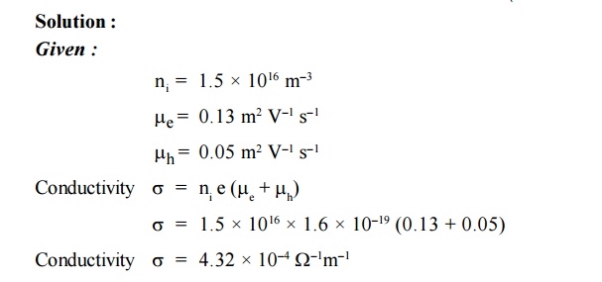 |
Q11) Explain the equation of state and write the equation of continuity?
A11)
Equations of state
We have studied separately modelled the primary types of carrier action taking place inside semiconductors. Within actual semiconductors all the various types of carrier action occur at the same time, and the state of any semiconductor can be determined only by taking into account the combined effect of the individual types of carrier action. "Putting it all together leads to the basic set of starting equations employed in solving device problems known as the equations of state.
Continuity Equations
Each and every type of carrier action—whether it be drift, diffusion, indirect or direct thermal recombination, indirect or direct generation, or some other type of carrier action—gives rise to a change in the carrier concentrations with time. The combined effect of all types of carrier action can therefore be taken into account by equating the overall change in the carrier concentrations per unit time 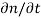 or
or 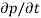 to the sum of the time
to the sum of the time 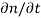 or
or 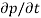 due to the individual processes; that is,
due to the individual processes; that is,
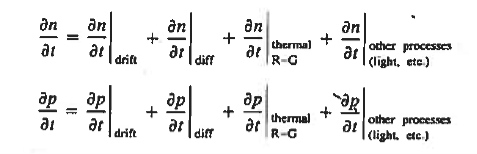
|
The overall effect of the individual processes is established by applying the requirement of conservation of carriers. Electrons and holes cannot mysteriously appear and disappear at a given point, but must be transported to or created at the given point via some type of on-going carrier action. There must be a spatial and time continuity in the carrier concentrations.
For this reason, Eqs. (1) are known as the continuity equations. The continuity equations can be written in a somewhat more compact form by noting
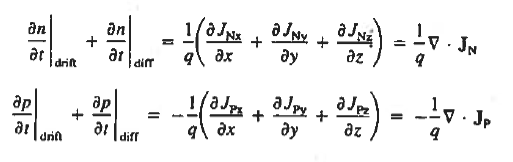
|
Equations (2), which can be established by a straightforward mathematical manipulation, merely state that there will be a change in the carrier concentrations within a given small region of the semiconductor if an imbalance exists between the total carrier currents into and out of the region.
Using Eqs. (2), we obtain
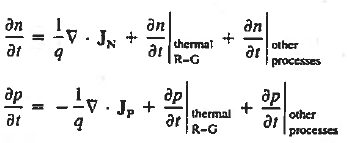 |
The (3) continuity equations are completely general and directly or indirectly constitute the starting point in most device analyses.
In computer simulations the continuity equations are often employed directly. The continuity equations are typically utilized only in an indirect fashion.
Q12) Derive minority carrier diffusion equation?
A12)
The "workhorse" minority carrier diffusion equations are derived from the continuity equations by invoking the following set of simplifying assumptions:
(I) The particular system under analysis is one-dimensional; i.e., all variables are at most a function of just one coordinate (say the x-coordinate).
(2) The analysis is limited or restricted to minority carriers.
(3) =0 in the semiconductor or regions of the semiconductor subject to analysis.
(4) The equilibrium minority carrier concentrations are not a function of position. In other words, n0  n0(x), p0
n0(x), p0  p0(x)
p0(x)
(5) Low-level injection conditions prevail.
(6) Indirect thermal recombination—generation is the dominant thermal R—G mechanism.
(7) There are no "other processes," except possibly photo generation, taking place within the system.
Working on the continuity equation for electrons, we note that
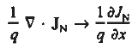 ………….. (1)
………….. (1)
If the system is one-dimensional. Moreover,
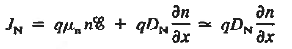 ………….. (2)
………….. (2)
When = 0 and one is concerned only with minority carriers. The drift component can be neglected in the current density expression because is small by assumption and minority carrier concentrations are also small, making the n product extremely small.
Since by assumption n0 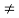 n0(x), and by definition n
n0(x), and by definition n 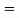 n0 +
n0 +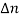 , we can also write
, we can also write
 ………….. (3)
………….. (3)
Combining Eqs. (1) through (3) yields
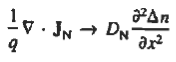 ………….. (4)
………….. (4)
Turning to the remaining terms in the continuity equation for electrons, the assumed dominance of recombination—generation via R—G centers, combined with the low-level injection and minority canter restrictions, allows us to replace the thermal R—G term as
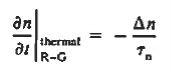 ………….. (5)
………….. (5)
In addition, apply (7) yields
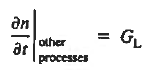 ………….. (6)
………….. (6)
Where it is understood that GL = 0 if the semiconductor is not subject to illumination. Finally, the equilibrium electron concentration is never a function of time, n0  n0(t), and we can therefore write
n0(t), and we can therefore write
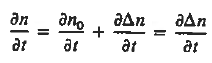 ………….. (7)
………….. (7)
Substituting Eqs. (4) through (7) into the continuity equation, and simultaneously recording the analogous result for holes, one obtains
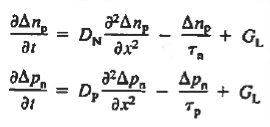 ………….. (8)
………….. (8)
This is known as Minority carrier diffusion equations. The equations are valid only for minority carriers, applying to electrons in p-type materials and to holes in n-type materials.
Common Diffusion Equation simplification is given below
Q13) Derive Einstein Relationship?
A13)
The formula between the D's and the μ's known as the Einstein relationship.
To simplify the development, we consider one dimensional system. The sample under analysis is taken to be a non-degenerate, non-uniformly doped semiconductor maintained under equilibrium conditions.
The net carrier currents must be identically zero under equilibrium conditions, and focusing on the electrons, we can state
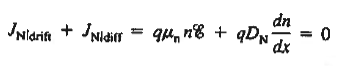 ……….. (1)
……….. (1)
However,
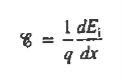 ……….. (2)
……….. (2)
And
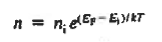 ……….. (3)
……….. (3)
Moreover, with dEF/dx=0 (due to the positional invariance of the Fermi level under equilibrium conditions),
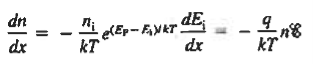 ……….. (4)
……….. (4)
Substituting dn/dx from Eq. (4) into Eq. (1) and rearranging the result slightly. One obtains
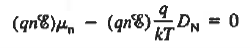 ……….. (5)
……….. (5)
Since 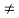 0 (a consequence of the nonuniform doping), it follows from Eq. (5) that
0 (a consequence of the nonuniform doping), it follows from Eq. (5) that
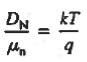 ……….. (6)
……….. (6)
The above equation (6) is known as Einstein Relationship for electrons. This equation hold for holes also
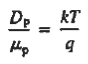 ……….. (7)
……….. (7)
The above equation (7) is known as Einstein Relationship for holes.
Although it was established while assuming equilibrium conditions, we can present more elaborate arguments that show the Einstein relationship to be valid even under non-equilibrium conditions.
The non-degenerate restriction however, still applies: slightly modified forms of Eqs. (7) result when the argument is extended to degenerate materials.
For Example
Relative to numerical values, note that kT/q is a voltage, and at room temperature (300 K) is equal to 0.0259V.
Hence, for an ND = 1014/cm3 Si sample maintained at room temperature,
DN = (kT/q) μn = (0.0259)(1358 cm2 /N-sec) = 35.2 cm2 /sec
Q14) What do you mean by charge neutrality relationship?
A14)
The relationships established an explicit dependence on the dopant concentrations introduced into a semiconductor. It is the charge neutrality relationship that provides the general tie between the carrier and dopant concentrations.
To establish the charge neutrality relationship. Let us consider a uniformly doped semiconductor. Systematically examining little sections of the semiconductor far from any surfaces, and assuming equilibrium conditions prevail, one must invariably find that each and every section is charge-neutral, it, contains no net charge. If this were not the case, electric fields would exist inside the semiconductor.
The electric fields in turn would give rise to carrier motion and associated currents—a situation totally inconsistent with the assumed equilibrium conditions.
There are, however, charged entities inside all semiconductors. Electrons, holes, ionized donors (donor atoms that have become positively charged by donating an electron to the conduction band) and negatively-charged ionized acceptors an all exist simultaneously inside any given semiconductor.
For the uniformly doped material to be everywhere charge-neutral require
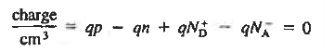 ………… (1)
………… (1)
Or
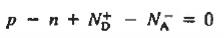 ………… (2)
………… (2)
Where, by definition.
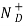 = Number of ionized (positively charged) donors/cm3.
= Number of ionized (positively charged) donors/cm3.
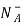 = Number of ionized (negatively charged) acceptors/ cm3.
= Number of ionized (negatively charged) acceptors/ cm3.
There is sufficient thermal energy available in a semiconductor at room temperature to ionize almost all of the shallow-level donor and acceptor sites.
Defining
ND = total number of donors/ cm3.
NA = total number of acceptors/ cm3
And setting
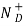 = ND
= ND
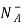 = NA
= NA
We obtain
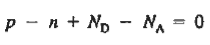 …………. (3)
…………. (3)
This assumes total ionization of dopant atoms. Equation (3) is the standard forms of the charge neutrality relationship.
Q15) What do you mean by Fermi function? Discuss the effect of temperature of on Fermi function?
A15)
The Fermi function gives the probability of occupying an available energy state, but this must be factored by the number of available energy states to determine how many electrons would reach the conduction band. This density of states is the electron density of states, but there are differences in its implications for conductors and semiconductors. For the conductor, the density of states can be considered to start at the bottom of the valence band and fill up to the Fermi level, but since the conduction band and valence band overlap, the Fermi level is in the conduction band so there are plenty of electrons available for conduction. In the case of the semiconductor, the density of states is of the same form, but the density of states for conduction electrons begins at the top of the gap.
Fermi function F (E):
Fermi-Dirac distribution function represents the probability of an electron occupying a given energy level at absolute temperature. It is given by
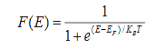
Where KB Boltzmann Constant
T Temperature
If g(E) is the density of states and f(E) gives the probability of occupation of those states at a given temperature, the number of occupied states, n(E),is given by
n(E) = 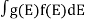 (1)
(1)
If the number of occupied states in an energy band needs to be calculated the integration needs to be performed over the entire band. This will be a function of temperature, since the Fermi function is temperature dependent. Equation 1 can be used to calculate the concentration of electron and holes in semiconductors, which decides their conductivity.
Effect of temperature on Fermi Function:
Case (i) Probability of occupation for E < EF at T = 0K
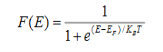
When T = 0K and E < EF, we have
F(E) = 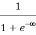 =
= 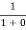 = 1
= 1
Thus at T = 0K, there is 100 % chance for the electrons to occupy the energy levels below the Fermi level.
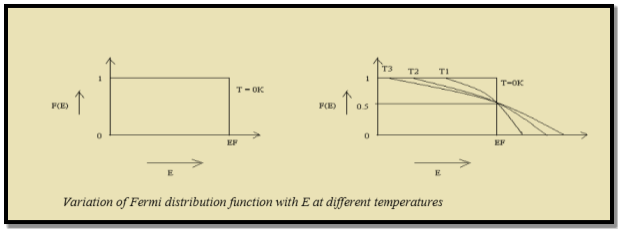 |
Figure 12: Fermi distribution
Case (ii) Probability of occupation for E>EF at T = 0K
When T = 0K and E > EF, we have
F(E) = 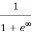 =
= 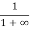 =
=  = 0
= 0
Thus, there is 0 % chance for the electrons to occupy energy levels above the Fermi energy level. From the above two cases, at T = 0K the variation of F(E) for different energy values becomes a step function.
Case (iii) Probability of occupation at ordinary temperature
At ordinary temperature, the value of probability starts reducing from 1 for values of E slightly less than EF. With the increase of temperature, i.e., T> 0K, Fermi function F (E) varies with E.
At any temperature other than 0K and E = EF
F(E) =  =
= 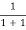 =
=  = 50%
= 50%
Hence, there is 50 % chance for the electrons to occupy Fermi level. Further, for E > EF the probability value falls off rapidly to zero.
Case (iv) At high temperature
When kT >> EF, the electrons lose their quantum mechanical character and Fermi distribution function reduces to classical Boltzmann distribution
Q16) Write a note on Density of states?
A16)
The energy band model indicated that the total number of allowed states in each band was four times the number of atoms in the crystal. But we don’t have idea about how the allowed states were distributed in energy; i.e., how many states were to be found at any given energy in the conduction and valence bands.
We are now interested in the energy distribution of states or density of states because the state distribution is an essential component in determining carrier distributions and concentrations.
The formula of the desired density of states is calculated using quantum-mechanical considerations. It is given by
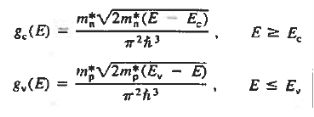 ……….(1)
……….(1)
Where gc(E) and gv(E) are the density of states at an energy E in the conduction and valence bands, respectively.
The density of states can be likened to the description of the seating in a football stadium, with the number of seats in the stadium a given distance from the playing field corresponding to the number of states specified energy interval froth Ec or Ev.
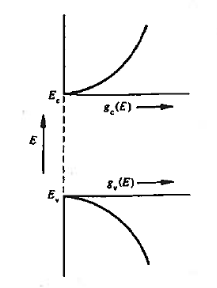 |
Figure 11: General energy dependence of gc(E) and gv(E) near band edges
gc(E) is zero at Ec and increases as the square root of energy when one proceeds upward into the conduction band.
Similarly, gv(E) is precisely zero at Ev, and increases with the square root of energy as one proceeds downward from Ev, into the valence band.
Also note that differences between gc(E) and gv(E) stem from differences in the carrier effective masses. If m*n were equal to m*p, the seating (states) on both sides of the football field (the band gap) would be mirror images of each other. Finally, considering closely spaced energies E and E+ dE in the respective bands, one can state
gc(E) dE represents the number of conduction band states/cm3 lying in the energy range between E and E + dE (if E  Ec),
Ec),
gv(E)dE represents the number of valence band states/cm3 lying in the energy range between E and E + dE (if E 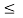 Ev),
Ev),
It therefore follows that gc(E) and gv(E) themselves are numbers /unit volume-unit energy, or typically, numbers/cm3- eV.
Q17) Explain the term doping in detail?
A17)
DOPING
The process by which an impurity is added to a semiconductor is known as Doping. The amount and type of impurity which is to be added to a material has to be closely controlled during the preparation of extrinsic semiconductor. Generally, one impurity atom is added to 108 atoms of a semiconductor.
Doping is basically manipulation of Carrier Numbers.
Doping is the addition of controlled amounts of specific impurity atoms with the express purpose of increasing either the electron or the hole concentration.
To increase the electron concentration, one can add either phosphorus, arsenic, or antimony atoms to the Si crystal, with phosphorus followed closely by arsenic being the most commonly employed donor (electron-increasing) dopants.
To increase the hole concentration, one adds either boron, gallium, indium, or aluminium atoms to the Si crystal, with boron being the most commonly employed acceptor (hole-increasing) dopant.
To understand how the addition of impurity atoms can lead to a manipulation of carrier numbers, it is important to note donors are all from Column V in the Periodic Table of Elements, while all of the acceptors are from Column III in the Periodic Table of Elements.
When a Column V element with five valence electrons is substituted for a Si atom in the semiconductor lattice, four of the five valence electrons fit snugly into the bonding structure. The fifth donor electron, however, does not fit into the bonding structure and is weakly bound to the donor site. At room temperature this electron is readily freed to wander about a lattice and hence becomes a carrier. Please note that this donation (hence the name "do-nor") of carrier electrons does not increase the hole concentration. The donor ion left behind when the fifth electron is released cannot move, and there is no broken atom—atom bonds associated with the release of the fifth electron.
The Column III acceptors have three valence electrons and cannot complete one of the semiconductor bonds when substituted for Si atoms in the semiconductor lattice. The Column III atom, however, readily accepts (hence the name "acceptor") an electron from a nearby Si—Si bond, thereby completing its own bonding scheme and in the process creating a hole that can wander about the lattice. Here again there is an increase in only one type of carrier. The negatively charged acceptor ion (acceptor atom plus accepted electron) cannot move, and no electrons are released in the hole-creation process.
 |
Figure 7: Visualization of (a) donor and (b) acceptor action using the bonding model.
The dopant action is reasonably understandable with the help of bonding-model. We noted that the fifth donor electron was rather weakly bound and readily freed at room temperature. Here the term "weakly bound" simply means that it takes =1 eV to break Si—Si bonds and very few of the Si—Si bonds are broken at room temperature.
Now try to figure it out with te help of energy band. Let us concentrate first on the binding energy of the fifth donor electron. Crudely speaking, the positively charged donor-core-plus-fifth-electron may be likened to a hydrogen atom. Conceptually, the donor core replaces the hydrogen-atom nucleus and the fifth donor electron replaces the hydrogen-atom electron.
In the real hydrogen atom the electron moves of course in a vacuum, can be characterized by the mass of a free electron and has a ground-state binding energy of — 13.6 eV.
In the pseudo-hydrogen atom, on the other hand, the orbiting electron moves through a sea of Si atoms and is characterized by an effective mass. Hence, in the donor or pseudo-atom case, the permittivity of free space must be replaced by the permittivity of Si and m0 must be replaced by m*n. We therefore conclude that the binding energy (EB) of the fifth donor electron is approximately
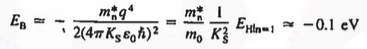 |
Where Ks is the Si dielectric constant (Ks = 11.8).
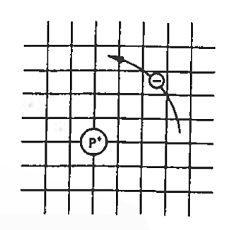 |
Figure 8: Pseudo hydrogen atom model for the donor-site bond.
When an electron is released from a donor it becomes a conduction band electron. If the energy absorbed at the donor is precisely equal to the electron binding energy, the released electron will moreover have the lowest possible energy in the conducting band—namely, EC. Adding energy 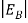 to the bound electron, in other words, raises the electron's energy to EC.
to the bound electron, in other words, raises the electron's energy to EC.
Hence, we are led to conclude that the bound electron occupies an allowed electronic level an energy 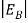 below the conduction band edge, or, as visualized in figure 9 donor sites can be incorporated into the energy band scheme by adding allowed electronic levels at an energy ED = EC -
below the conduction band edge, or, as visualized in figure 9 donor sites can be incorporated into the energy band scheme by adding allowed electronic levels at an energy ED = EC - 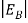 .
.
Note that the donor energy level is represented by a set of dashes instead of a continuous line, because an electron bound to a donor site is localized in space; i.e., a bound electron does not leave the general 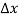 vicinity of the donor. The relative closeness of ED to EC of course reflects the fact that EC - ED =
vicinity of the donor. The relative closeness of ED to EC of course reflects the fact that EC - ED = 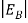 .
.
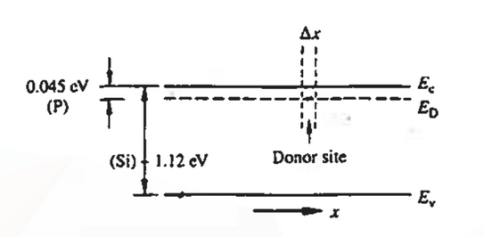 |
Figure 9: Addition of the E =ED donor slevels in the energy band diagram. Dashes of width  emphasize the localized nature of the bound donor-sites states.
emphasize the localized nature of the bound donor-sites states.
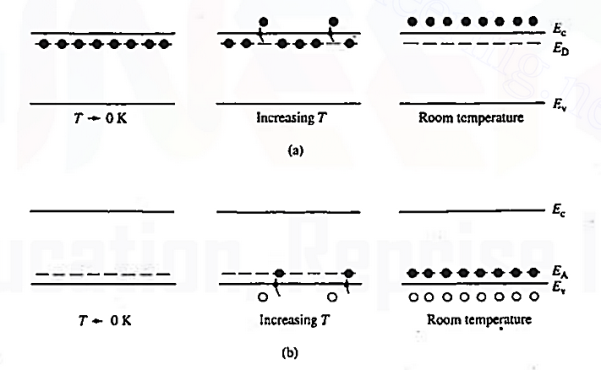 |
Figure 10: Visualization of (a) donor and (b) acceptor action using the energy baud model.
The actual visualization of dopant action using the energy band model is pictured in figure 10. Examining the left-hand side of Figure 10 (a), one finds all the donor sites filled with bound electrons at temperatures T 0K. This is true because very little thermal energy is available to excite electrons from the donor sites into the conduction band at these very low temperatures.
0K. This is true because very little thermal energy is available to excite electrons from the donor sites into the conduction band at these very low temperatures.
As the temperature is increased, the situation changes with more and more of the weakly bound electrons being donated to the conduction band. At room temperature the ionization of the donors is all but total, giving rise to the situation pictured at the extreme right of Figure 10(a).
The situation for acceptors is completely analogous. As visualized in Figure 10(b), acceptors introduce allowed electronic levels into the forbidden gap at an energy slightly above the valence band edge. At low temperatures, all of these sites will be empty—there is insuffient energy at temperatures T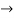 0 K for a valence band electron to make the transition to an acceptor site.
0 K for a valence band electron to make the transition to an acceptor site.
Increasing temperature, implying an increased store of thermal energy, facilitates electrons jumping from the valence band onto the acceptor levels. The removal of electrons from the valence band of course creates holes. At room temperature, essentially all of the acceptor sites are filled with an excess electron and an increased hole concentration is effected in the material.
An impurity that can act as either a donor or an acceptor is referred to as an amphoteric dopant.
The purpose of adding impurity in the semiconductor crystal is to increase the number of free electrons or holes to make it conductive.
If a Pentavalent impurity, having five valence electrons is added to a pure semiconductor a large number of free electrons will exist. Which make a n-type extrinsic semiconductor?
If a trivalent impurity having three valence electrons is added, a large number of holes will exist in the semiconductor. Which make a p-type extrinsic semiconductor?
Q18) Explain the term effective mass?
A18)
EFFECTIVE MASS
Mass of the carrier is one of the basic but important property. However, the carrier mass is not a simple property and cannot be easily defined by quoting a number.
We however already know the fact that effective mass not simple mass. "Effective" mass of electrons within a crystal is a function of the semiconductor material (Si, Ge, etc.) and is different from the mass of electrons within a vacuum.
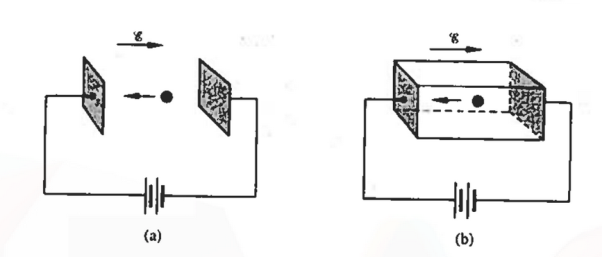 |
Figure 6: An electron moving in response to an applied electric field (a) within a vacuum, and (b) within a semiconductor crystal
Let us first consider the motion of electrons in a vacuum. An electron of rest mass m0 is moving in a vacuum between two parallel plates under the influence of an electric field , then, according to Newton's second law, the force F on the electron will be
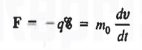 ……….. (1)
……….. (1)
Where v is the electron velocity and t is time.
Next consider electrons (conduction band electrons) moving between the two parallel end faces of a semiconductor crystal under the influence of an applied electric field, as envisioned in Figure 6(b).
Electrons moving inside a semiconductor crystal will collide with semiconductor atoms, thereby causing a periodic deceleration of the carriers. However, not Eq. (1) should not apply to the portion of the electronic motion occurring between collisions. Under the effect of applied electric field, electrons in a crystal are also subject to complex crystalline fields.
Thus the motion of carriers in a crystal can be described only by using Quantum Mechanics, the formalism appropriate for atomic-sized systems. Fortunately, if the dimensions of the crystal are large compared to atomic dimensions, the complex quantum mechanical formulation for the carrier motion between collisions simplifies to yield an equation of motion given below
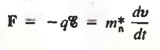 ………… (2)
………… (2)
Where m*n is the electron effective mass.
A similar equation can be written for holes with —q q and m*n
q and m*n  m*p.
m*p.
This is a very significant result. It allows us to conceive of electrons and holes as quasi-classical particles and to employ classical particle relationships in most device analyses.
Although the effective mass formulation is a significant simplification, it should be mentioned that the carrier acceleration can vary with the direction of travel in a crystal; i.e.. The effective masses can have multiple components. Moreover, depending on how a macroscopic observable is related to the carrier motion, a different grouping of mass components can lead to a different m* being utilized in a particular relationship.
There are, for example, cyclotron resonance effective masses, conductivity effective masses, density of states effective masses, among others. It is also probably not too surprising that the effective masses vary somewhat with temperature.
Q19) Write a note on carriers?
A19)
We already know that that there are no carriers or possible current flow if the bonding model has no broken bonds. Equivalently, in the energy band model, if the valence band is completely filled with electrons and the conduction band is devoid of electrons. There are no carriers or possible current flow. This lack of carriers and associated current flow is easy to understand in terms of the bonding model where the shared electrons are viewed as being tied to the atomic cores.
As accurately portrayed in the energy band model, however, the valence band electrons actually move about in the crystal. How is it then that no current can arise from this group of electrons? As it turns out, the momentum of the electrons is quantized in addition to their energy. Moreover, for each and every possible momentum state in a band, there is another state with an oppositely directed momentum of equal magnitude. Thus, if a band is completely filled with electrons, the net momentum of the electrons in the band is always identically zero. It follows that no current can arise from the electrons in a completely filled energy band.
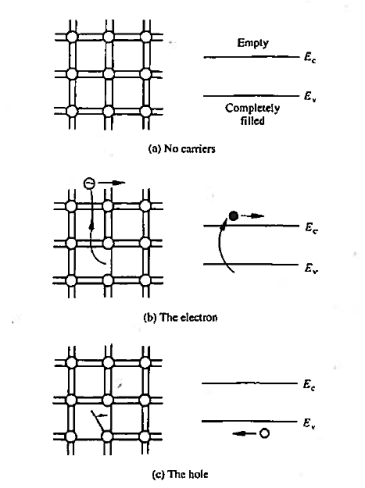 |
Figure 4: Visualization of carriers using the bonding model (left) and the energy band model (left) (a) No-carrier situation (b) Visualization of electrons (c) Visualization of hole.
The electrons that do give rise to charge transport are visualized in Figure above. When a Si—Si bond is broken and the associated electron is free to wander about the lattice, the released electron is a carrier. Equivalently, in terms of the energy band model, excitation of valence band electrons into the conduction band creates carriers; that is, electrons in the conduction band are carriers.
Note that the energy required to break a bond in the bonding model and the band gap energy are one and the same thing. Likewise, free bonding-model electrons and conduction band electrons are just different names for the same electrons.
In addition to releasing an electron the breaking of a Si-Si bond also creates a missing bond or void in the bonding structure.
By bonding modelled one can visualize the movement of this missing bond from place to place in the lattice as a result of nearby bound electrons jumping into the void
By the energy band model one can visualize the removal of an electron from the valence band creates an empty state in vast sea of filled stales. The empty slate in the valence band is the second type of carnet found in semi-conductors—the hole. Both electrons and holes participates in the operation of most semiconductor devices.
Q20) Explain Bonding Model?
A20)
The isolated Si atom was found to contain four valence electrons. A Si atom is not interacting with other atoms; Si atoms exhibit a bonding that involves an attraction between each atom and its four nearest neighbours.
The implication here is that in going from isolated atoms to the collective crystalline state, Si atoms come to share one of their valence electrons with each of the four nearest neighbours. This covalent bonding, or equal sharing of valence electrons with nearest neighbours, and the mere fact that atoms in the diamond lattice have four nearest neighbours, give rise to the idealized semiconductor representation, the bonding model, shown in Figure 1. This is giving two dimensional representation of the model.
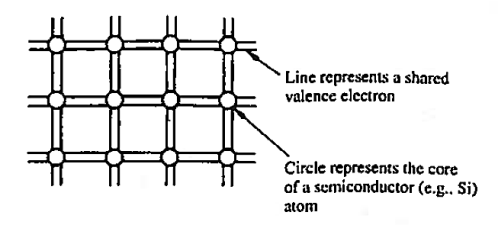 |
Figure 1: Bonding Model
Each circle in the bonding model represents the core of a semi-conductor atom, while each line represents a shared valence electron.
There are eight lines connected to each atom because any given atom not only contributes four shared electrons but must also accept four shared electrons from adjacent atoms.
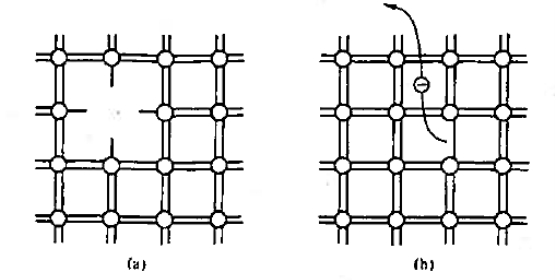 |
Figure 2: Bonding Model (a) Visualisation of misting atom or point defect (b) Breaking of an atom.to-atom bond and freeing of an electron.
With the help of bonding model, we can visualise the following factor as shown in figure 2. The bonding model is used to picture a point defect, a missing atom, in the lattice structure. It helps to visualise the breaking of an atom-to-atom bond and the associated release or freeing of an electron.
We know that Bond breaking occurs at high temperature (at T> 0 K) and defects occur naturally in all semiconductors.
The basic model shown in figure 1 is strictly valid for an entire semiconductor only at T = 0 K when the semiconductor contains no defects and no impurity atoms.
If we want to describe the spatial aspect of semiconductor only bonding model is not sufficient we need to know about the energy aspects too. So we will now see the energy band model.