Unit 1

Introduction to Signal and System

Q1) Define signal and system.

A1)

Signal

A signal is a description of how one parameter varies with another parameter.

For example:  voltage changing over time in an electronic circuit.

Picture brightness: A camera senses the incoming light and records the light reflectivity as a function of space onto a magnetic film.

System

A system is a process that produces an output signal in response to an input signal.

     Communication System

As illustrated in the figure system produces output signal in response to an input signal.

Q2) Explain continuous and discrete system

A2)

Continuous systems input and output continuous signals, such as analog electronics where the signal varies continuously with respect to time.

Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.

Q3) Explain classification of systems

A3)

Continuous –time System and Discrete Systems

A continuous time system is one which operates on the continuous time  input signal and produces a continuous-time output signal.

If the input is x(t) and output is y(t) then

y(t) = T{x(t)}

That is x(t ) is transformed to y(t).

Example : Amplifiers, filters, motors etc  

Discrete time system is one which operates on discrete time input signal and produces  a discrete-time output signal.

If the input is x(n) and output y(n) then

y(n) = T[x(n)]

Static and Dynamic Systems

A system is said to be static or memoryless if its output at any instant depends on the input at that instant but not on the past or future values of input.

Otherwise the system is dynamic or with memory.

Linear and Non-linear Systems.

Superposition principle states that the response to a weighted sum of input signals be equal to the weighted sum of the outputs corresponding to each of the individual input signals . A system that  satisfies the superposition principle is said to be linear system.

T [a1 x1(t) + a2 x2(t)] = a1 T[x1(t)] + a2 T[x2(t)]

∴, T [a1 x1(t) + a2 x2(t)] = a1 y1(t) + a2 y2(t)

Similarly for discrete –time linear system

T [ax1(n) + bx2(n)] = a T[x1(n) + bTx2(n)]

Time Variant and Time Invariant Systems

A system is said to be time-variant if its input-output characteristics does not change with time.

Suppose we apply a signal(t) to a system to a system and obtain an output y(t) as shown in the figure.

If we delay by T seconds then for a time-invariant system the output will be delayed by T seconds.

Causal and  Non-casual systems.

System is  said to be casual if its output depends on the present and past inputs and not on the future input.

If the output depends on the future inputs then it is non- casual system.

Invertible and Non-Invertible systems

A system is said to invertible if the input of the system appears at the output.

Y(S) = X(S) H1(S) H2(S)

= X(S) H1(S) · 1(H1(S))/ (H1( S))       Since H2(S) = 1/( H1(S) )

∴, Y(S) = X(S)

→ y(t) = x(t)

Hence, the system is invertible.

If y(t) ≠ x(t), then the system is said to be non-invertible.

Stable and Unstable Systems

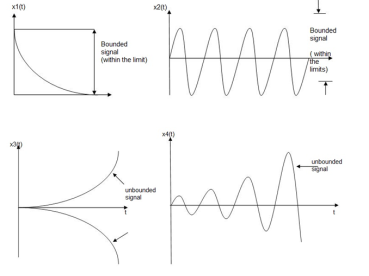
An input signal x(t) is said to be bounded if it satisfies the condition |x(t) |≤Mx < ∞ for all t.

Similarly, the output signal is bounded if it satisfies the condition |y(t)| ≤My < ∞

The example for bounded and unbounded signals is as shown in the figure.

Q4) Write a short note on standard test signal

A4)

We need to obtain the response of the signal for a specific input. But the question is, the input can be varying signal or sometimes random signal . Therefore some  standard test signals are required to know the performance of the system. Thus the standard input signals include:

• An impulse
• Step
• Ramp
• Parabolic input.

Impulse Signal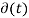

The impulse response is as shown in the figure.

• The impulse response is zero for t ≠ 0.
• It rises to infinity at t = 0– and comes back to zero at t = 0+ enclosing a finite area.
• If this area is A it is called as an impulse function of strength A.
• If A = 1 it is called a unit impulse function.

Thus, an impulse signal is denoted by f(t) = A (t).

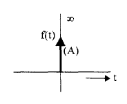
Step Signal

The step signal is as shown in the figure.

• For t<0 it is zero.
• For t=0 it rises to A
• For t>0 it remains the same.

Thus, the step signal is denoted by f(t) = A u(t). If A=1 it is called unit step function.

Ramp Signal

The ramp signal is as shown in the figure.

• For t<0 it is zero.
• Uniformly increases with slope = A .

It is denoted by f(t) = At . If the slope is unity then it is called a ramp signal.

Unit Parabolic Signal

A unit parabolic signal, p(t) is defined as,

p(t) =  t2/2;      t≥0

=0;t<0 and t=0

We can write unit parabolic signal p(t) in terms of unit step signal  u(t) as

P(t) = t2/2 u(t).

The following figure shows the unit parabolic signal.

Q5) Explain the properties of the system

A5)

Periodicity

The signal’s behaviour/graph repeats after every T. Therefore,

x(t) = x(t + nT) or

x(t) = x(t – nT)

Where, T is the fundamental period. So we can say that the signal remains unchanged when shifted by multiples of T.

Even and Odd

An even signal is symmetric about the Y-axis.

x(t) = x(-t) even

x(t) = - x(-t) odd

The signal can be broken into even and odd parts by

x(t) = x(t + nT)

x(t) = x (t – nT)

Time Invariant

Any delay provided in the input must be reflected in output for time invariant system

Take x2(t) = x(t –T)

Then y(x2(t)) must be x2(y(t))

Here x2(t) is a delayed input.

We see that  if there is  a delayed input through the system is the same  delay is in the output signal.

y(t) = e x(t)

y(t) = ex(t-T)

y(t-T) = ex(t-T)

y(t) = y(t-T)

System is in-variant.

Q6) Explain the properties of linearity

A6)

There are the properties

 Homogeneity

 Additivity

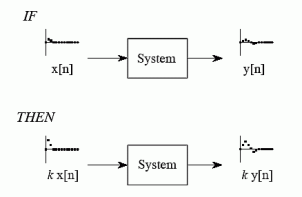
Homogeneity

Homogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.

That is a change in x[n]  will result in a change in y [n]

Also a change in k x[n] will result in a change in k y[n]

Additivity

Consider a system where input x1[n] produces an output y1[n]. Similarly x2[n]  produces y2[n].

The system is additive when

x1[n] + x2[n] = y1[n] + y2[n]

In other words signals added at the input will produce signals added at the output.

Q7) Explain the property of stability and causality

A7)

BIBO stability

Bounded input bounded output stability.

The system is BIBO stable if

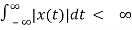
Causality

Causal signals are signals that are zero for all negative time. If any value of the output signal depends on a future value of the input signal then the signal is non-causal.

Example

Y(t) = ½[x(t) – x(-t)]

For negative values of t the output depends on future values of input

Q8) Explain the property of shift variance

A8)

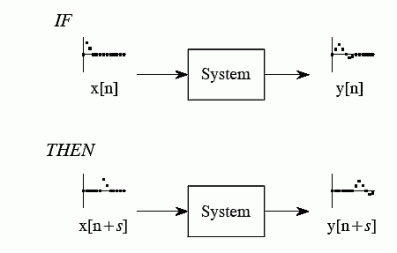
Shift Invariance

Shift invariance means that a shift in the input signal will result in an identical shift in the output signal

If x[n]  -> y[n]

Then x[n+s] -> y[n +s] for any constant s

Q9) Check whether the systems is casual or not.

A9)

y(n) = x(n) + 1/x(n-1)

For n=0

y(0) = x(0) + 1/x(0 -1)

For n=1

y(1) = x(1) + 1/ x(0)

For n=2

y(2) = y(2) + 1/x(1)

For n=-1

y(-1) = x(-1) + 1/x(-2)

Q10) Find the even and odd of the signal as shown in the figure

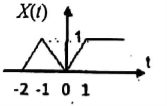
A10)

Step 1: Find the signal x(-t)

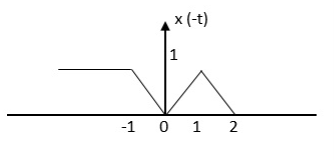
The even signal is xe(t) = x(t) +x(-t)

Therefore

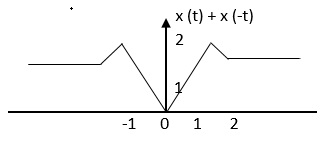
Xe(t) = ½ x(t) +x(-t)/2

For odd the signal is

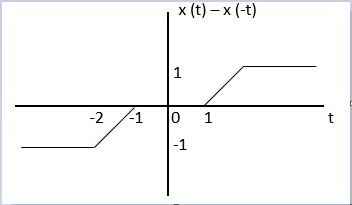
Xo(t)