Unit 3
Laplace Transformation
Q1) Explain Laplace transform
A1)
Consider an LTI system by a complex exponential signal of the form
x(t) = Gest.
Where s = any complex number = σ+jω
σ = real of s, and
ω = imaginary of s
The response of LTI can be obtained by the convolution of input with its impulse response i.e.
y(t)=x(t)×h(t)=
Where H(S) = Laplace transform of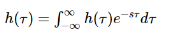 
Similarly, Laplace transform of 
Q2) Find the Laplace transform of
f(t) = cos wt
A2)
f(t) = (1/2) e jwt + (1/2) e – jwt
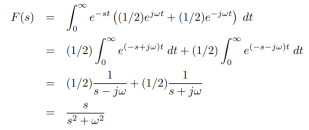
Q3) Explain the properties of Laplace transform
A3)
Linearity
If there are two signals f and g and a is scalar, then
L(af) = a F.
L(f + g) = F + G
That is homogeneity and superposition holds good.
Time Scaling
Definition:
If g(t ) = f(at) then where a>0 then
G(s) = 1/a F(s/a)
Here the time is scaled by a therefore frequency by 1/a
G(s) =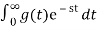 
G(s) =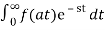 
G(s) =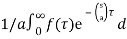
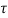
G(s) = 1/a F(s/a)
L(e at) = 1/a(1/(s/a) – 1)
L (e at ) = 1/s-a.
Exponential Scaling
Definition:
Let f be a signal and a be scalar then
g(t) = e at f(t) then
G(s) = F(s-a) .
G(s) = 
G(s) = 
G(s) = 
G(s) =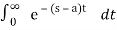 
= F(s-a)
Derivative
If the signal f is continuous at t=0 then
L(f) = s F(s) – f(0).
- Time-domain differentiation becomes multiplication by frequency variable s
- The initial condition is –f(0).
For higher order derivatives apply the formula twice that is
L(f’’) = s L(f’) – f’(0)
= s (sF(s) – f(0)) – f’(0)
= s2 F(s) – s f(0) – f’(0)
Integral
Let g be the running integral of signal f
g(t)=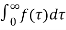 
then
G(s) = 1/s F(s)
That is the time-domain integral becomes division by frequency variable s.
Q4) Find the Laplace transform of sin wt
A4)
L(sin wt) =- 1/w d/dt coswt
L(sin wt) = -1/w ( s s/s2 + w2 - 1 )
= w / s2 + w2
Q5) Explain shift theorem
A5)
First shifting theorem:
This theorem states that
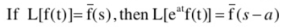
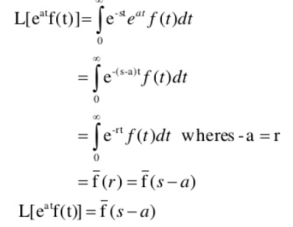
Similarly,
Second Shift Theorem
If L{f(t)} = F(s) and g(t) = {f(t-a) t>a }
0 t<a
Then L{g(t)} = e-as F(s)
Proof:
g(t) = f(t-a) t>0
0 t<0
Proof:
L{g(t)} =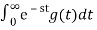 
= 
+ 
= 
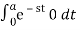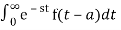
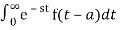
Let z =t-a or t = z+a ; dt = dz.
When t=a z =0;
t = ∞ z = ∞ ;
Therefore,
L { g(t) }=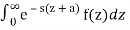 
L{g(t)}=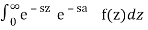 
= 
= 
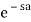
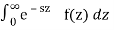
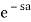L { f(z)}
L{ g(t) } =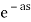 
L { f( t-a)}
= 
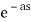F(s)
Q6) Find the Laplace transform if
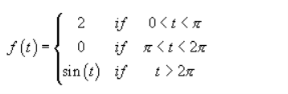
A6)
Can be written as
The Laplace transform can be written as
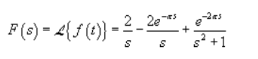
Q7) Find the Laplace transform of periodic signals.
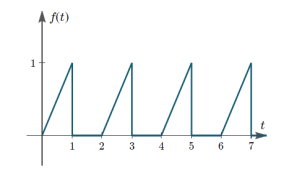
A7)
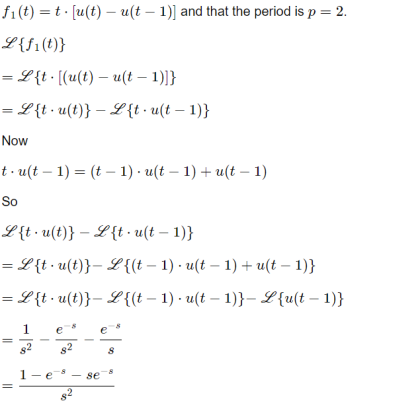
Hence, the Laplace transform of the periodic function, f(t) is given by:
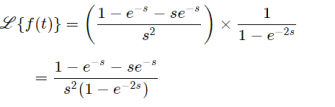
Q8) Explain initial and final value theorem
A8)
Initial value theorem and Final value theorem are together called as Limiting Theorems.
Conditions for the existence of Initial value theorem
- The function f(t) and its derivative f(t) should be Laplace transformable.
- If time t approaches to (0+) then the function f(t) should exists.
The function f(t) = 0 for t > 0 and contains no impulses or higher order singularities at origin.
If f(t) and F(s) is Laplace transform pairs.
That is
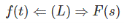
Then Initial value theorem is given by
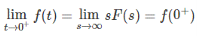
Proof
Laplace transform of a function f(t) is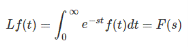
then Laplace transform of its derivative f ‘ (t) is
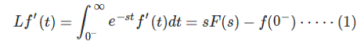
Consider the integral part first
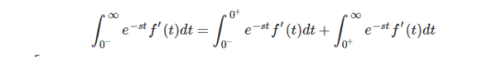
[lim s->∞ e -st is indeterminate and hence splitted into two integrals
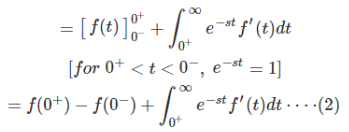
Substituting (2) in (1) we get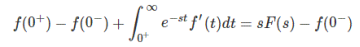
Upon cancelling f (0–) on both sides we get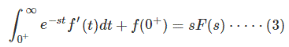
On considering (s) tends to infinity on both sides in (3)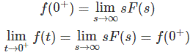
Hence, Initial value theorem is proved.
Final value theorem
If f(t) and f'(t) both are Laplace Transformable, and sF(s) has no pole in jw axis and in the R.H.P. (Right half Plane) then,
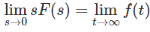
Proof
We know differentiation property of Laplace Transformation: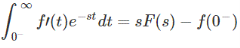
Now we take limit as s → 0. Then e-st → 1 and the whole equation looks like
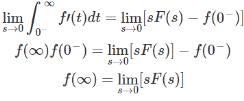
If sF(s) has poles on the right side of s plane.
If sF(s) has conjugate poles on jw axis.
If sF(s) has pole on origin.
Then apply
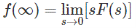
Q9) For the circuit given find i1 and i2.
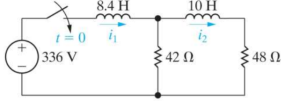
A9)
Electrical & Elect
For t> 0
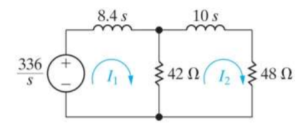
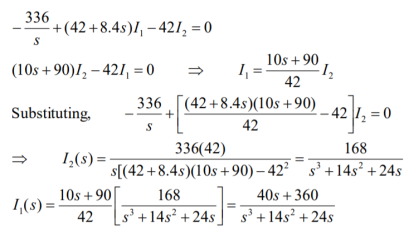
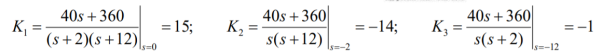
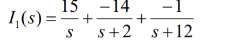
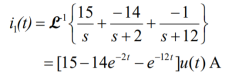
The forced response is 15 u(t) A
The natural response is [-14 e -2t – e -12t ] u(t) A
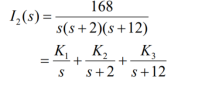
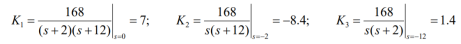
The forced response is 7 u(t) A;
The natural response is [ -8.4 e -2t – 1.4 e -12t ] u(t) A
Q10) Explain the properties of ROC
A10)
Property 1:
The ROC of X(s) consists of strips parallel to the jΩ – axis in the s-plane.
Property 2.
ROC does not contain any poles.
Property 3.
If x(t) is of finite duration and is absolutely integral then ROC is the entire s-plane.
Property 4:
If x(t) is a right sided signal that x(t) = 0 for t<to <∞ then ROC is of the form Re(s) > 
max. Where 
max equals to the maximum real part of any poles of X(s).
Property 5:
If x(t) is left-sided that is x(t) =0 for t>t1 >- ∞. Then the ROC is of the form Re(s) < >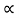 
min.
Property 6:
If x(t) is two-sided than the ROC is of the form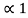 
< Re(s) < 
.
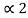Q11) Solve the following IVP
y′′−10y′+9y=5t,y(0)=−1y′(0)=2y″−10y′+9y=5t,y(0)=−1y′(0)=2
A11)
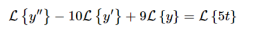
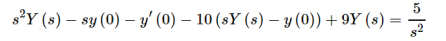
Plug in the initial conditions we get
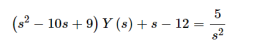
Solve for Y(s)
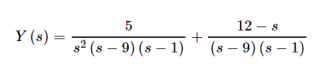
Combining the two terms we get
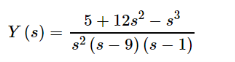
The partial fraction decomposition for this transform is,
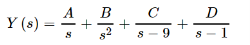
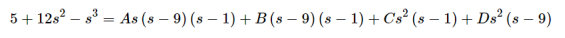
Taking the inverse transform gives us the solution to the IVP.
