Unit 5

Z- transformation

Q1) Explain the z-transform of discrete time signal.

A1)

The Z transform for discrete time system x(n ) is defined as

X(z) = 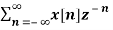   ------- (1) where z is a complex variable.

In polar form z can be expressed as

z  = r e jw ---------------(2) where r is the radius of a circle.

For n≥ 0

X(z ) = 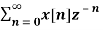       --------- (3)which is called one-sided z-transform.

By substituting z = r e jw

X(r e jw) = 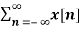   (r e jw) –n     ------- (4)

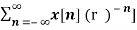          e- jwn       ----- (5)

Equation(5) represents the Fourier transform of the signal x(n) r-n

Hence the inverse DTFT  X(r ejw) must be x(n) r-n.

x(n) r-n = 1/2π 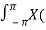r e jw )  e jwn dw

On multiplying both sides by rn  we get

x(n) = 1/ 2 π 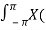  r ejw) (r ejw ) n dw                [ z = r ejw

Let z= r e jw  and dw= dz/jz

Dz = r ejw dw

Dw = dz/jre jw

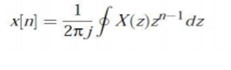
1. If X(z)= 4 – 5 z-2 + z-3 – 2z -4    then find x[n]

Solution:

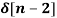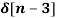x[n] = 4 - 5 + - 2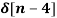

Q2) Explain z-transform with respect to LTI system

A2)

For discrete time LTI system with Impulse response h[n]

For input z n

The output response y[n] = H(z) z n

Where

H(z) = 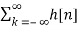  z -n

The Z-transform of general discrete time signal x[n] is defined as

X(z) = 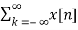  z -n

Q3) Find the impulse response and step response for the following systems:

A3)

y(n) = -  ¾ y(n-1) + 1/8 y(n-2) = x(n)

y(n)  - ¾ y(n-1) + 1/8 y(n-2) = x(n)

Taking z-transform on both sides we get

Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)

Substituting y(-1)=y(-2)= 0

Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

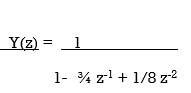
Impulse response

x(n) =        X(z) =1

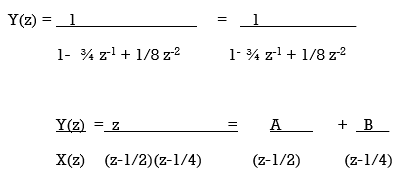
By solving A=2 and B=-1.

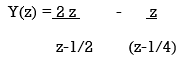
            y(n) = 2 (1/2)n u(n) – (1/4) n u(n).

Step Response

x(n) = u(n)X(z) = z/z-1

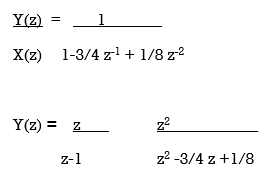
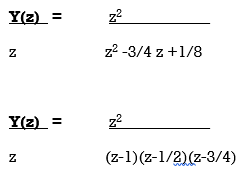
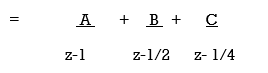
By solving A=8/3   B= -2  C= 1/3

Therefore

Y(z) = 8 . z      -2 z   + 1/3 z

3    z-1     z-1/2z-1/4

y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)

Q4) Explain the application of z-transform to open loop system

A4)

Consider the following diagrams:

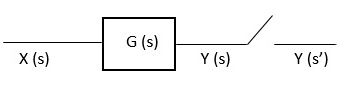
Y( s) = [Y(s)]*

Y(s) = [ X(s) G(s)]*

= [X G(s)]*

Taking z-transform on both sides we get

Y(z) = XG(z)

Y(s) = G1(s) G2(s) X*(s)

Y*(s) = [Y(s)]*

= X*(s) [G1(s)G2(s)]*

= X*(s) [G1G2(s)]*

Y(z) = X(z) G1G2(z)

Q5) Explain the properties of ROC

A5)

Properties of Region of Convergence

1. The ROC is a ring or disk in z-plane centered at the origin.
2. The ROC cannot contain any poles.
3. If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.
4. If x(n) is a finite duration anti-casual sequence then the ROC is the entire z-plane except at z=∞.
5. If x(n) is a finite duration two- sided sequence the ROC is entire z-plane except at z=0 and z=∞.
6. If x(n) is infinite duration two- sided sequence ROC will consist of a ring in z-plane bounded on the interior and exterior by a pole not containing any poles.
7. The ROC of an LTI stable system contains the unit circle

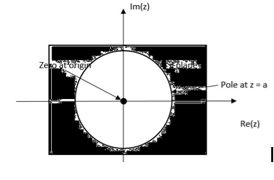
Q6) Find the z-transform and ROC of the signal

x(n) = an u(n)

A6)

X(z) =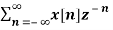 

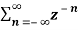       = an u(n) -----(1)u(n) = 0 for n<0

1 for n≥0

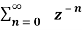= an ------- (2)

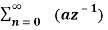= n   ------- (3)

This is a geometric series of infinite length that is

a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1

          Then from equation (3) it converges when |az-1| < 1 or |z| >|a|

Therefore

X(z) = 1/ 1-az-1:  ROC    |z| > |a|

Q7) Find the direct form 1 for the equation

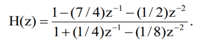
A7)

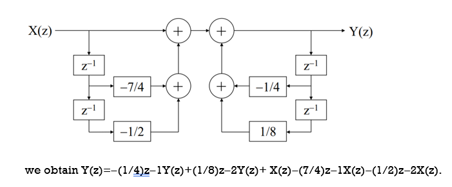
Q8) Find the direct II form for the equation

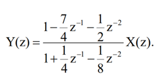
A8)

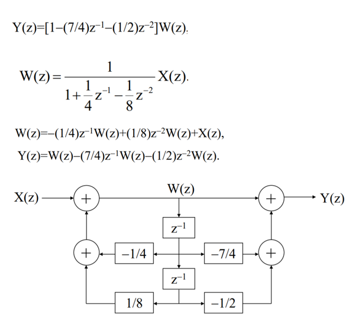
Q9) Explain the applications of Z-transform

A9)

Z transform is used to convert discrete time domain signal into discrete frequency domain signal. It has wide range of applications in mathematics and digital signal processing.
It is mainly used to analyze and process digital data. For example, to analyze JPEG images, MP3 and MP4 songs, ZIP files etc, we can make use of Z transform.
Applications of Z transform in digital signal processing are,

1. Used in system designing

2.Used to find out stability of a system

3.Used to find frequency response of a signal

4.Analysis of linear discrete system

5.For designing digital filters.