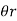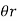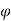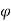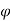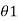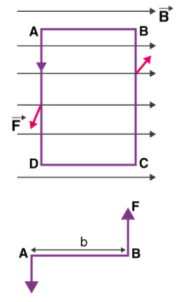
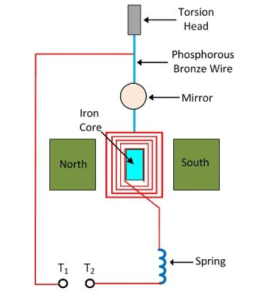
Figure 1 D’Arsonval Galvanometer | unit 3 galvanometer

Electronics Instruments and Measurement

Unit-3Galvanometer Q1) Explain the construction of D’Arsonal Galvanometer?A1)

Figure 1 D’Arsonval Galvanometer The construction of galvanometer consists of

Moving coil:

It is the current carrying element. It is either rectangular or circular in shape and consists of several turns of fine wire. This coil is suspended so that it is free to tum about its vertical axis of symmetry. It is arranged in uniform, radial, horizontal magnetic field in the air gap between pole pieces and armature (iron core) of a permanent magnet. The armature (iron core) is spherical in shape if the coil is circular but is cylindrical if the coil is rectangular. 2. Damping There is a damping torque present owing to production of eddy currents in the metal former on which the coil is mounted. Damping is also obtained by connecting a low resistance across the galvanometer terminals. 3. Suspension The coil is supported by a fiat ribbon suspension which also carries current to the coil. The other current connection in a sensitive galvanometer is a coiled wire. This is called the lower suspension and has a negligible torque effect. This type of galvanometer must be levelled carefully so that the coil hangs straight and centrally without rubbing the poles or the soft iron cylinder. 4. Indication. The suspension carries a small mirror upon which a beam of light is cast. The beam of light is reflected on to a scale upon which the deflection is measured. This scale is usually about 1 metre away from the instrument, although 1 /2 metre may be used for greater compactness. Q2) Explain the working principle of the galvanometer?A2) Let a current I flow through the rectangular coil of n number of turns and a cross-sectional area A. When this coil is placed in a uniform radial magnetic field B, the coil experiences a torque τ.Initially consider a single turn ABCD of the rectangular coil having a length l and breadth b. This is suspended in a magnetic field of strength B such that the plane of the coil is parallel to the magnetic field.Since the sides AB and DC are parallel to the direction of the magnetic field, they do not experience any effective force due to the magnetic field. The sides AD and BC being perpendicular to the direction of field experience an effective force F given by F=BI.l

Figure 2. Current carrying loop in magnetic field. We know that torque τ = force x perpendicular distance between the forcesτ = F × bSubstituting the value of F we already know,Torque τ acting on single-loop ABCD of the coil = BIl × bWhere lx b is the area A of the coil,Hence the torque acting on n turns of the coil is given byτ = nIABThe magnetic torque thus produced causes the coil to rotate, and the phosphor bronze strip twists. In turn, the spring S attached to the coil produces a counter torque or restoring torque kθ which results in a steady angular deflection.Under equilibrium condition:kθ = nIABHere k is called the torsional constant of the spring (restoring couple per unit twist). The deflection or twist θ is measured as the value indicated on a scale by a pointer which is connected to the suspension wire.θ= ( nAB / k)ITherefore θ ∝ I Q3) Explain the construction of vibration galvanometer?

Figure 3. Vibration GalvanometerThe figure shows the construction of Duddell’s Moving coil galvanometer. The moving coil consists of fine bronze or platinum silver wire. This wire passes over small pulley at top and is pulled tight by a spring attached to the pulley , the tension of the spring can be adjusted by turning a milled head attached to the spring. The loop of wire is stretched over two ivory bridge pieces the distance between these pieces is adjustable. When the moving coil vibrates due to passage of a.c the reflected beam from the mirror throws a band of light upon a scale provided for this purpose. Tuning: Tuning means adjustment of the natural frequency of the moving system so that it is equal to the frequency of the current passing through the coil. Tuning is done by varying the distance between the bridge pieces. This varies the length of the loop which is free to vibrate and thus varies the natural frequency of the moving system. Fine adjustment is done by varying the tension of the spring. When the galvanometer is tuned the amplitude of vibrations is very large and consequently a very wide band of light is observed on the scale. Q4) Derive the expression for ballistic galvanometer?

Let us consider a rectangular-shaped coil consists of ‘N’ number of turns kept in a constant magnetic field. The length and breadth are ‘l’ and ‘b’. So, the area of the coil is

A = l × b

When current flows across the coil, then the torque is developed . The magnitude of the torque is given by τ = NiBA

Assume that the flow of current across the coil for each minimal time is dt and so the change in current is represented as

τ dt = NiBA dt

When there is current flow across the coil for a time of ‘t’ seconds, then the value is represented as

ʃ0t τ dt = NBA ʃ0t idt = NBAq

where ‘q’ is the total amount of charge that flows across the coil. The inertial moment that exists for the coil is shown as ‘I’ and the coil’s angular velocity is shown as ‘ω’.

The below expression provides the angular momentum of the coil and it is lω. It is like the pressure that is applied to the coil.

By multiplying the above two equations, we get

lw = NBAq

Also, the kinetic energy across the coil will have deflection at ‘ϴ’ angle and the deflection will be restored using the spring. It is represented by

Restoring torque value = (1/2)cϴ2

Kinetic energy value = (1/2)lw2

As the coil’s restoring torque is similar to the deflection then

(1/2)cϴ2 = (1/2)lw2

cϴ2 = lw2

Also, the periodic oscillations of the coil is shown as below

T = 2π√(l/c)

T2 = (4π2l/c)

(T2/4π2) = (l/c)

(cT2/4π2) = l

Finally, (ctϴ/2π) =lw = NBAq

q = (ctϴ)/NBA2π

q = [(ct)/NBA2π] * ϴ)

Assume that k = [(ct)/NBA2π

Then q = k ϴ

So, ‘k’ is the constant term of the ballistic galvanometer.

Q5) Explain the construction of ballistic galvanometer?

The ballistic galvanometer consists coil of copper wire which is wound on the non-conducting frame of the galvanometer. The phosphorous bronze suspends the coil between the north and south poles of a magnet. For increasing the magnetic flux the iron core places within the coil. The lower portion of the coil connects with the spring. This spring provides the restoring torque to the coil.When the charge passes through the galvanometer, their coil starts moving and gets an impulse. The impulse of the coil is proportional to the charges passes through it. The actual reading of the galvanometer achieves by using the coil having a high moment of inertia. The moment of inertia means the body oppose the angular movement. If the coil has a high moment of inertia, then their oscillations are large. Thus, accurate reading is obtained. Q6) The scale of galvanometer is placed at a distance of 0.4m from the mirror . A deflection of 44mm is observed. What is the angle through which the coil has turned?Suppose d is the deflection and r is the distance between scale and mirror and

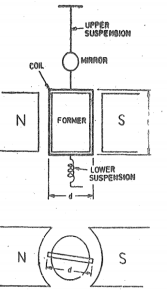
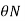is the angle turned through by the mirror then d = 2 r

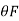= d/2r = 44 x 10 -8 / 2 x0.4 = 55 x 10 -3 rad Q7) The coil of moving coil galvanometer is wound on non-magnetic former whose height and width are both 2cm. It moves in constant field of 0.12 Wb/m2. The moment of inertia of its moving parts 0.25x 10 -5 kg-m2 and the control spring constant is 30 x 10 -6 Nm/rad. Calculate the number of turns that must be wound on the coil to produce a deflection of 150 o with current of 10mA.

Final steady deflection = 150

Current i=10mA

Constant spring constant K = 30 x 10 -6 Nm/rad

Final steady deflection = Gi/K

Displacement constant G = KF /I = 30 x 10 -6 x (5/6) π/ 10 x 10 -3 = 2.5 π x 10 -3 Nm/A

But displacement constant G = NBld

Number of turns N = G/BlD = 2.5 π x 10 -3 / 0.12 x 0.02 x 0.02 = 164

Q8) A D’Arsonal galvanometer has a rectangular coil wound on an aluminium former of resistivity 27 x 10 -9 Ω-m. The sides of the former each of effective length move in a radial field of uniform flux density 0.15Wb/m2 against control torque 18 x 10 -6 Nm/rad. The width of the former is 20mm the ends being effectively outside the magnetic field and the moment of inertia of the moving system is 80 x 10 -9 kg-m2.

Total damping factor in the absence of all other damping except the damping produced by former is

D = G2 / N2 Rt = N2 B2 I 2 d2 / N2 Rt

For critical damping

B2 I 2 d2 / Rt = 2 √ K J

Hence resistance of former Rt = B2 I 2 d2 / 2 √ K J

= (0.15) 2 x (30 x 10-3) 2 x (20 x 10-3) 2 / 2 √ 18 x 10 -6 x 80 x 10 -9 = 3375

Q9) A moving coil ballistic galvanometer of 150Ω resistance gives a throw of 75 divisions when the flux through search coil to which it is connected is reversed. Find the flux density in which the reversal of the coil takes palce given that the galvanometer constant =110μC/div and the search coil has 1400 turns a mean area of 5000mm2 and resistance of 20 Ω. Calculate the ballistic and flux linkage sensitivites of the galvanometer.

The resistance of the galvanometer circuit = 20 + 150 = 170 Ω

Galvanometer constant Kv= 10 μC/div

Now

Kq = Q/ = it / 1 = et / R

But changes in flux linkages ∆ = 2

e = 2 /t = 2 ɸN/t = 2 BAN/t

Hnece Kq = 2 BAN/t . t/ R = 2BAN/ RQ1

Flux density B = KqR 2AN = 110 x 10 -6 x 170 x 75 / 2 x 5000 x 10 -6 x 1400= 0.1 Wb/m2

Ballastic sensitivity Sv= 1/Kq = 1/110 = 9.1 x 10 -3 div/μC = 9100 div/C

Flux linkage sensitivity = Sɸ = Sq/R = 9100/150 = 60 weber turn/div

Q10) A ballistic galvanometer gives the first maximum deflection of 60 o discharge of 1000μC. Find the quantity of electricity when discharged through the galvanometer gives rise to spot deflection of 10 divisions on a millimetre circular scale 1 metre away.

Let us assume that angular deflection of 60 o is the deflection of the reflected ray from the mirror attached to the moving coil

Charge Q = Kq = 60 = π/3 rad

Kq = 1000/ π/3 = 3000/π μ C/rad

Angle turned through the reflected ray for a swing of 10mm is = l/r = 10/1000 =0.01 rad

Charge for a swing of 0.01 radian is Q = 3000/π x 0.01 = 9.56 μ C

Sign Up