Unit - 1

Introduction and Modeling of control system

Q1) Find SFG for the block diagram below?

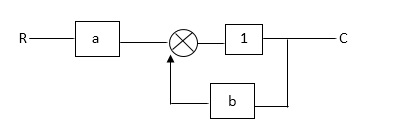
A1)

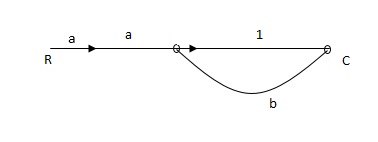
Ra+cb =c

c/R= a/1-b

Q2) The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1­?

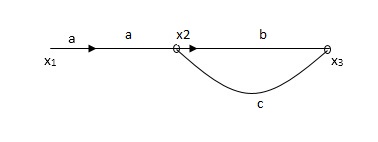
A2)

X1- I/p node

X2-Intenmediale node

X3- o/p node

Ab- forward path (p)

Bc- 1 loop (L)

At node XQ:

X2 = x1a + x3c [Add i/p signals at  node]

At node x3:

x2b =x3

(x1a+x3c) b = x3

X1ab = x3 (1-bc)

X1 = x3 (1-bc)/ab

Ab/(1-bc) = x3/x1

T= p/1-L

X1:- I/p node    x2, x3,x4,x5,Qnlexmedili node

X0:- o/p node  abdeg:- forward path

Bc, ef :- Loop [isolated] 

x2 = ax1+c x3

x3= bx2

x4 = d x3+f x5

x5 = e x4

x6= g x5

x6 = g(e x4) = ge [dx3+ e f x5]

xb = ge [d (bx2) + f (e x4)]

xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]

xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+

f( e [db (ax1+ cx3)

x2 = ax1 + cb (x2)  x4 = d bx2 + f exq

x2 = ax1 + cbx2          = db (d4) + fe/1-cb

x2 = ax1/(1-cb)   xy = db x2 + f x6/g

xy = db [ax1]/1-cb + f xb/g

x5 = c db ( ax1)/1-cb + efxb/g

xb = gx5

= gedb (ax1)/1-cb + g efxb/g

Xb = gx5

Gedb (ax1)/1-cb + g efxb/g

(1-gef/g) xb = gedb ax1/1-ab

Xb/x1 = gedb a/ (1- ef – bc + beef

Xb/x1 = p/ 1- (L1+L2) + L1 L2 for isolated loops

Q3) Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?

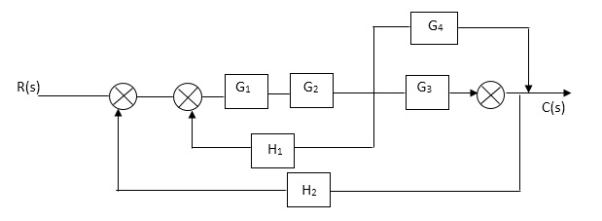
A3)

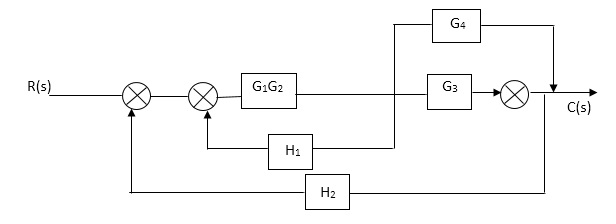
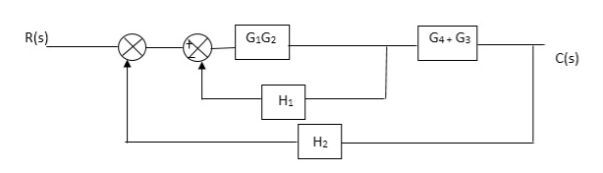
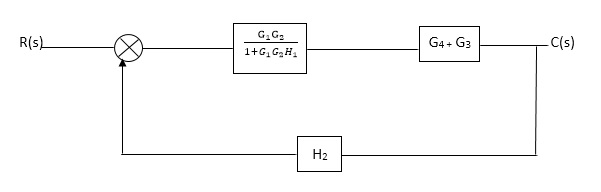
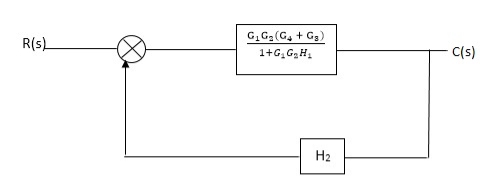
Fig. Final reduced block diagram

C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1

= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)

=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)

C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2

Q4) Reduce using Masons gain formula

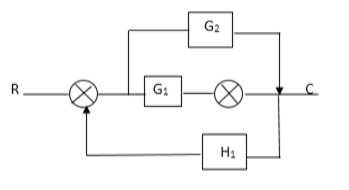
A4)

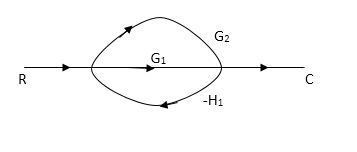
P1= G1 p2 =G2 Delta1 =1

L1= -G1 H1

= 1-(-G1H1)

= 1+G1H1

T= G1+G2/1+G1H1

Q5) Determine overall gain reliably x5 and x1 Draw SFG

X2 = ax1+ f x2

X3= bx2 +exy

X4 = cx3+hx5

X5 =dx4 + gx2

A5)

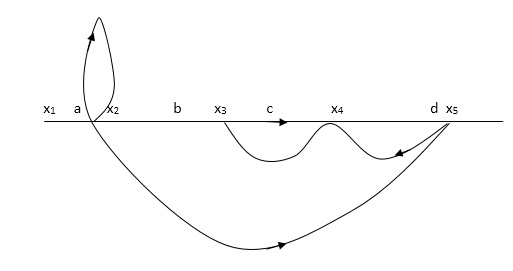
P1 = abcd       p2 = ag

L1 = f   L2 = ce, L3= dh

1 = 1

2= 1-ce

= 1-[L2+L2+L3] + [L1 L2 +L1 L3]

= 1-[f+ le = dh] + [fce +fdh]

T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)

Q6) Draw the free body diagram and write the differential equation for system below.

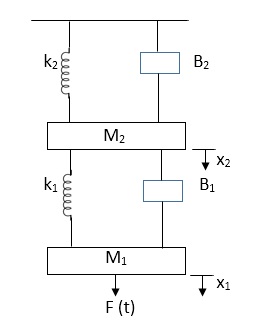
A6)

The free body diagram for M1 will be

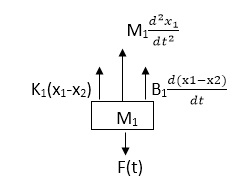
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)

Similarly for M2we have

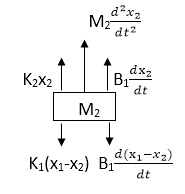
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt

Q7) For the given mechanical system below draw the analogus system (force. Voltage) & find V0(s)/V1(s)

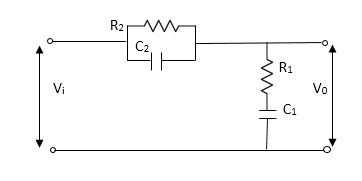
A7)

Let     Z1   = R2 11 1/c2

=R2*1/c2s/R2+1/c2s

Z1= R2/1+R2c2s

Let     Z2 = R1+1/c1s

Z2= 1+R1c1s/c1s

V0(s)/vi(s) = z2/z1+z2

= 1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s

V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2

Q8) Differentiate between AC and DC Tachometer?

A8)

Q9) What are magnetic amplifiers, explain its working and types?

A9)

They are basically electromagnetic device used for amplification of electrical signals. The basic working of this amplifier depends on the saturation of core principle. It consists of two cores connected in opposite phases, with control and AC winding. By applying small amount of DC currents on control winding large amount of current on AC winding can be controlled.  They are of two types

a)     Half wave magnetic amplifier: When DC supply is given to the control winding the magnetic flux is generated in the iron core. As flux increases the output impedance decreases and the current through AC winding in output increases. Here only half cycle of AC is utilised.

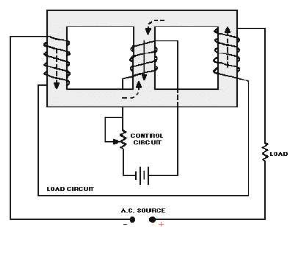
If the current through the control winding is zero, then the impedance of the output winding will be very high making no current to flow through the load or output winding. A diode is connected to the output winding which acts as a rectifier, used for reversing the polarity of the AC supply constantly from cancelling out control winding flux.

b)    Full wave magnetic amplifier: It utilizes both the half cycles of the AC supply. Due to wound of the two halves of the output winding the direction of magnetic flux created by these two halves in centre leg is same as direction of control winding flux                                         

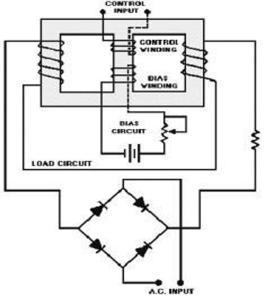
No control voltage is supplied there will be some flux present in magnetic core, hence impedance of the output winding will never attain its maximum value and current through load never attain its minimum value. The operation of the amplifier can be controlled by using the bias winding.

Q10) Explain force-voltage analogy?

A10)

If the dynamic characteristics of an electrical system is identical to that of a mechanical system, then the electrical system is said to be analogous to the mechanical system. This can be done by comparing the mathematical models of both the systems.

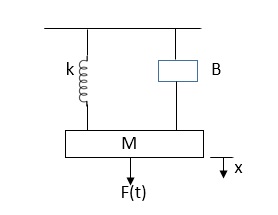
Fig. Mechanical System

The equation for above mechanical system is given by

f(t) = M 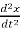+B 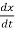+kx                                     (1)

For series RLC circuit the mathematical equation is given as

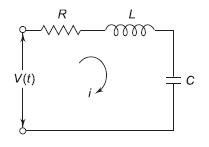
Fig. Electrical System

V(t)= Ri + L +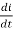

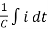
i =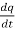 

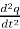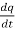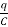V(t) = L + R +                                           (2)

Comparing 1 and 2 we see that

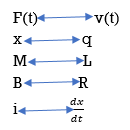
Q11) Explain force-current analogy?

A11)

For parallel RLC circuit shown below the KCL equation is written as

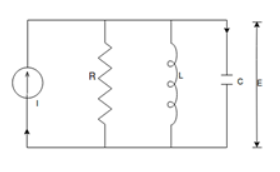
Fig. Electrical Circuit

i(t) = C + +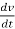

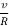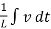
v =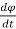 

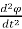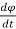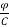i(t) = C + R +                          (3)

Comparing 1 and 3 we find that

Q12) Reduce the give block diagram to find the transfer function?

A12)

The above block diagram can be reduced as shown below

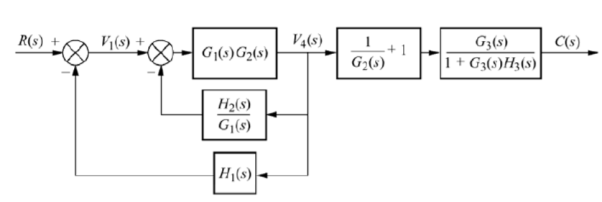
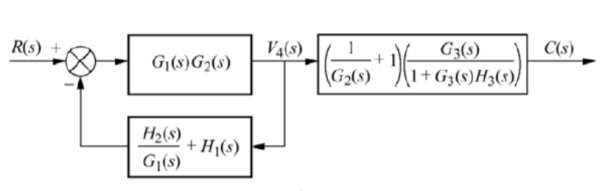
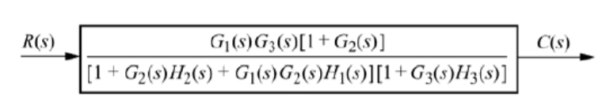
From above reduced figure the transfer function is very clear.

Q13) Reduce the given figure using block diagram reduction to find its transfer function?

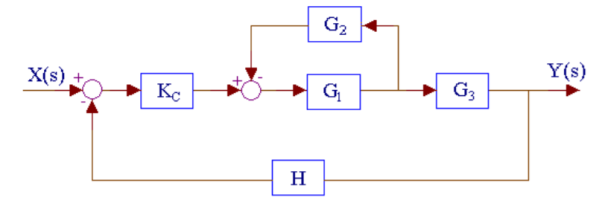
A13)

The above system can be reduced as

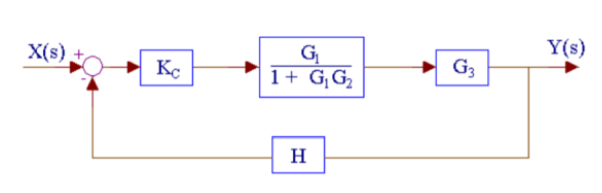
Kc, (G1/1+G1G2) and G3 are in series. H is in feedback with them.

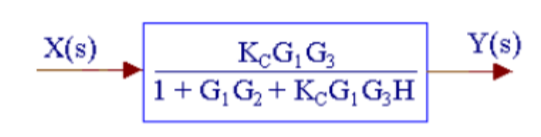
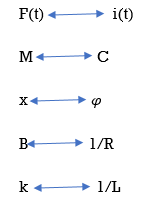
Q14) Reduce the given system using block diagram reduction technique?

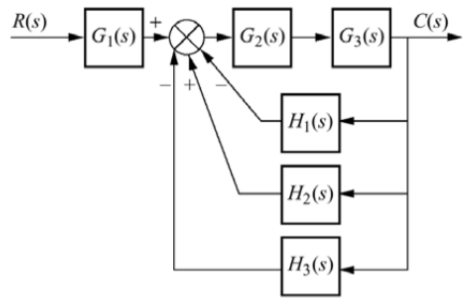
A14)

The figure can be reduced as

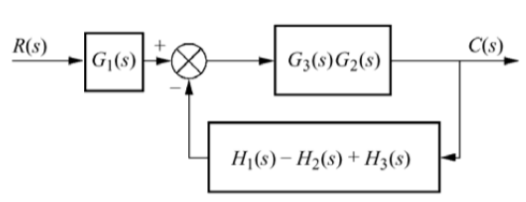
G1 and G2 are in series and H1, H2 and H3 are in parallel.

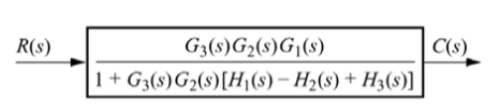
G1 is in series with feedback configuration. The transfer function becomes

C(s)/R(s) =

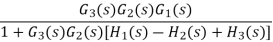
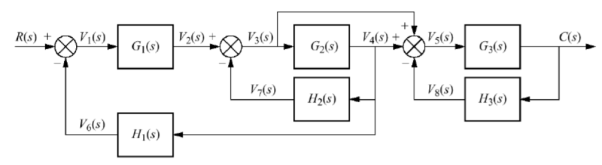
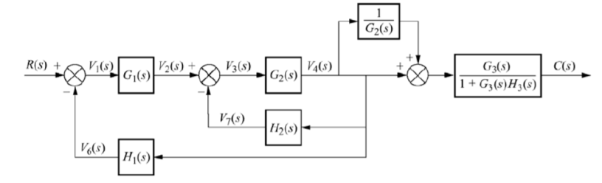
Q15) Compute the transfer function of the given figure?

A15)

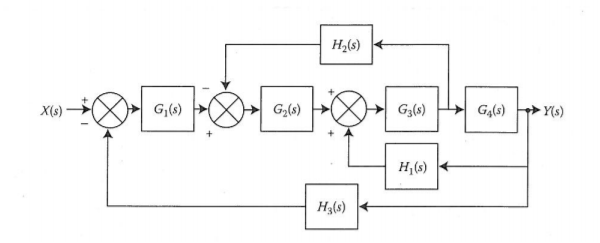
The branch point at the left of the block with transfer function G4(s) is moved at the right of G4(s). The equivalent block diagram is

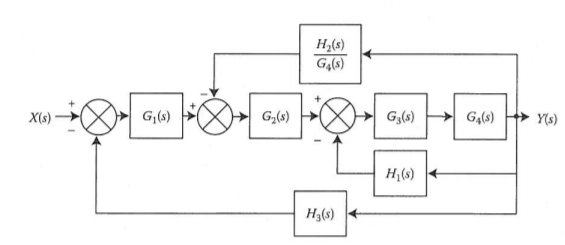
The transformation is applied to blocks with transfer function G3(s), G4(s) and H1(s).

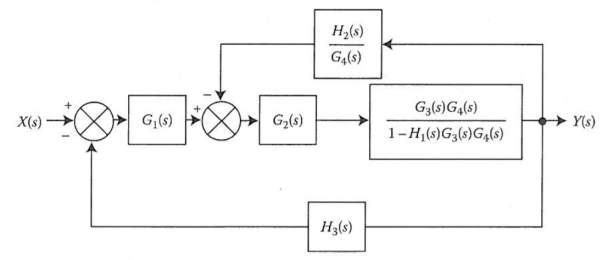
We apply transformation to the loop with TF H2(s)/G4(s) we get

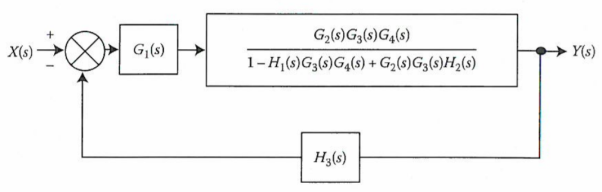
Again, applying same transformation to above figure we get the final reduced structure

Q16) Derive the transfer function of thermal system?

A16)

Thermal systems are those that involve the transfer of heat from one substance to another. The model of thermal systems is obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.

Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.

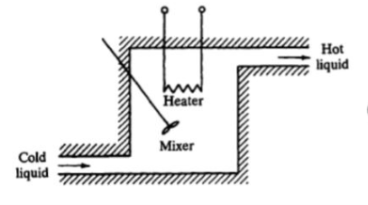
Fig. Thermal System

Let        θ1 = Steady state temperature of inflowing liquid, °C 

θ0 = Sandy state temperature of outflowing liquid, °C 

G = Steady state liquid flow rate, Kg/sec 

M = Mass of liquid in tank, Kg 

c = Specific heat of liquid, Kcal/Kg °C 

R = Thermal resistance, °C - sec/Kcal 

C = Thermal capacitance, Kcal/°C 

Q = Steady state heat input rate, Kcal/Sec 

Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1. Due to this, the heat output flow rate will gradually change from Q to Q + q0. The temperature of the outflowing liquid will also be changed from θ0  to  θ0 + θ.

For this system the equation for q0, C and R is obtained as follows,

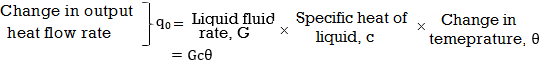
Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc 

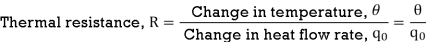
On substituting for qo from equation (1) in equation (3) we get, 

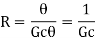
In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.

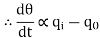
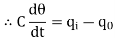
The constant of proportionality is capacitance C of the system.

Equation (5) is the differential equation governing system. Since, equation (5) is of first order equation, the system is first order system.

From equation (3),   R = θ/q0  

q0 = θ/R

On substituting for q0 from equation (6) in equation (5) we get,

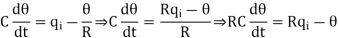
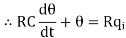
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s) 

On taking Laplace transform of equation (7) 

RC s θ(s) + θ(s) = R Q1(s)

θ(s) [sRC + 1] = R Q1(s)

 θ(s)/Q1(s)  is the required transfer function of thermal system.

Q17) Write short note on hydraulic system and also mention its types?

A17)

The Hydraulic system of interest to control engineers may be classified into, 

1.Liquid Level system

2.Hydraulic devices 

The liquid level system consists of storage tanks and connecting pipes. The variables to be controlled are liquid height in tanks and flow rate in pipes. The driving force is the relative difference of the liquid heights in the tanks. The Hydraulic devices are devices using incompressible oil as their working medium. In this we will be learning transfer function of hydraulic system.  

These devices are used for controlling the forces and motions. The driving force is the high-pressure oil supplied by the Hydraulic pumps. Liquids are slightly compressible at high pressures.

In hydraulic system, the compressibility effects may be neglected and conservation of volume is used as the basic physical law. The variables of hydraulic system are volumetric flow rate, q and pressure, R The volumetric flow rate, q is through variable and it is analogous to current. The pressure, P is across variable and it is analogous to voltage.

Three basic elements of hydraulic systems are the Resistance, Capacitance and lnertance. The liquid flowing out of a tank can meet the resistance in several ways. Liquid while flowing through a pipe meet with resistance due to the friction between pipe walls and liquid. Presence of valves, bends, coupling of pipes of different diameter also offer resistance to liquid flow.

The capacitance is an energy storage element and it represents storage in gravity field. The inertance represents fluid inertia and is derived from the inertia forces required to accelerate the fluid in a pipe. It is also an energy storage element. But the energy storage due to inertance element is negligible compared to that of capacitance element.

Consider the flow through a short pipe connecting two tanks. The Resistance, R for liquid flow in such a pipe or restriction, is defined as the change in the level difference, necessary to cause a unit change in the flow rate. 

R = Change in level difference/Change in flow rate

The Capacitance, C of a tank is defined to the change in quantity of stored liquid necessary to cause in the potential (head). 

C = Change in liquid stored/Change in head

A simple liquid level system is shown in the below figure with steady flow rate, Q and steady state head, H.

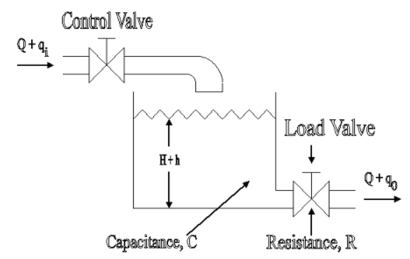
Fig. Liquid Level System

Let Q = Steady state flow rate(before any change has occured)

Qi = Small deviation of inflow rate from its steady-state value

Qo = Small deviation of outflow rate from its steady-state value  

H = Steady state head (before any change has occurred

h = Small deviation of head from its steady state value

Let the system be considered linear. The differential equation governing the system is obtained by equating the change in flow rate to the amount stored in the tank. In a small time interval dt, let the change in flow rate be (qi - qo) and the change in height be dh.

Now, Change In storage = Change in flow rate 

C dh = (qi – q0) dh 

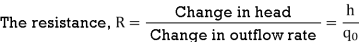
q0 = h/R

On substituting for q0, we get ,

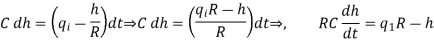 RC dh/dt + h = qi R

The above equation is the differential equation governing the system.The term RC is the time constant of the system .On the Laplace's transform of above equation we get,

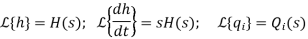
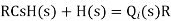
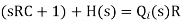
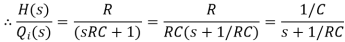
The above equation is the required transfer function of the Hydraulic system.

Q18) Explain servomechanism and ac servomotor with torque speed characteristics?

A18)

Servomechanism is also called servo which is a device usually error sensing device connected as a feedback element to correct the action of a mechanism. Here instead of controlling a device by variable input signal, the device is controlled by feedback signal.

The input signal applied to such systems generate the required output which is compared again to the input signal. If the device achieves its desired output, there will be no longer the logical difference between the two signals. Hence, the primary task of servomechanism is to maintain the output of a system at the desired value in the presence of disturbances.

A.C. Servomotors:

A.C servomotor is a two-phase ac induction motor. There are two windings in this motor, one is fixed or reference winding is supplied with a fixed voltage and frequency from a constant voltage source. Second winding is control winding with variable supply voltage of same frequency as reference winding but having a phase displacement of 900 electrical. A flux is induced due to the phase change which cuts the conducting bars of rotor and causes a time varying current, this current produces a time varying flux and reacts with the stator flux causing the rotor to rotate.

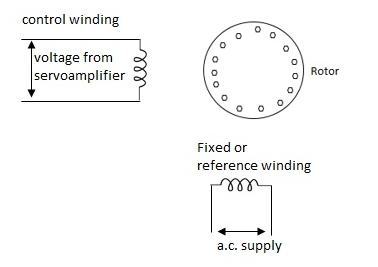
Fig. AC Servomotor

The rotor of A.C. Servo motors are of two types,

(a). Squirrel Cage Rotor

(b). Drag cup type rotor

(a). Squirrel cage rotor: They have high resistance as the rotor is having large length and small diameter. The air gap here is kept small.

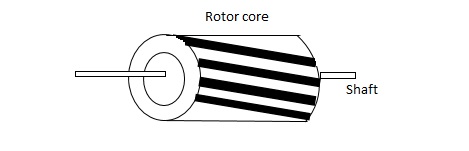
Fig. Squirrel cage rotor

(b). Drag cup type motor: For the drag cup rotor there are two air gaps. For the rotor a cup of non-magnetic conducting material is used. A stationary iron core is placed between the conducting cup to complete the magnetic circuit. The resistance of drag cup type is high and therefore, has high starting torque. Generally aluminium is used for cup.

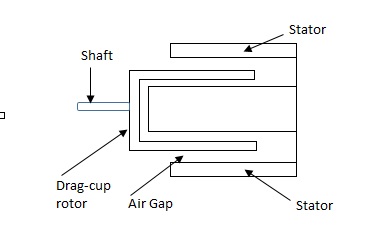
Fig. Drag Cup type rotor

Torque-speed characteristic:

The torque speed characteristics of the two phase servomotor depends on ratio of reactance to resistance(X/R).

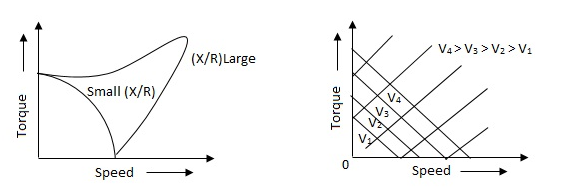
Fig. The torque speed characteristics of the two phase servomotor

(i). For high ‘R’ and low X, the characteristic is linear and

(ii). For high X and low R, it becomes non-linear.

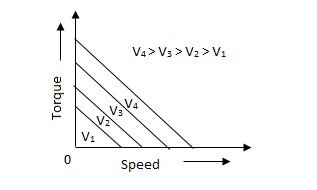
Fig. Torque-speed characteristic for various voltage

The torque-speed characteristic for various voltage is almost linear.

Q19) What are tachometers and list the difference between its types?

A19)

These are electromechanical devices which convert mechanical input at their shaft to corresponding electrical output. It is basically used to measure speed of motor. It has negative feedback. These devices are most commonly used to find speed of any rotating machine.

Q20) Explain synchros transformer?

A20)

Its basic working principle is similar to the synchro transformer. Here the rotor is cylindrical type. It is an electromechanical device. The combination of synchro transmitter and synchro transformer is used as an error detector.

The basic diagram is shown below,

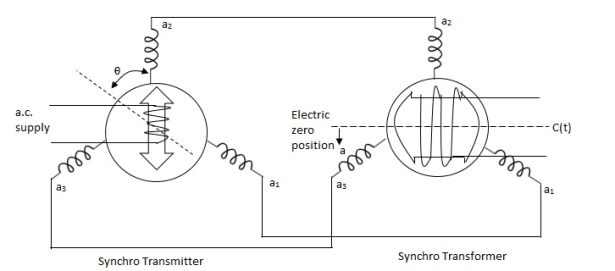
Fig. Synchros Transformers 

Let transmitter rotate at an angle ϴ and control transformer rotor rotate in same direction through α. Then,

φ = ( 90 - ϴ + α )

Voltage across rotor terminal is given as,

e(t) = K1Vrcos ϴSinwot

e(t) = K1VrSin(ϴ - α) Sin wot

From above equation we can conclude that when two rotor shafts are not aligned, the rotor voltage of transformer is a sine function of difference between two angles.

For small angular displacement between two rotor position

e(t) = K1Vr(ϴ - α)Sinwot