Unit - 6
Power Electronics Applications
Q1) A three phase fully controlled bridge converter operating from a 3-phase 220V, 50Hz supply is used to charge a battery bank with nominal voltage of 240V. The battery bank has internal resistance of 0.01Ω and the battery bank voltage varies by ± 10% around its nominal value between fully charges and uncharged condition. Assuming continuous conduction find out:
- The range of firing angle of the converter
- The range of ac input power
- The range of charging efficiency.
A1) When the battery bank is charged with constant average charging current of 100Amps through a 250mH lossless inductor.
The maximum and miminum battery voltages are VB(min) = 0.9 x VB Nom = 216 volts
And VB (max) = 1.1 x VB Nom = 264 volts.
Since the average charging current is constant 100A.
Vo (max) = V B max + 100 x RB = 264 + 100 x 0.01 = 265 volts
Vo (min) = VB (min) + 100 x RB = 216 + 100 x 0.01 = 217 volts.
But Vo max = 3√ 2/ π VL cos α min ; α min = 26.88
Vo min = 3√ 2/ π VL cos α max α max = 43.08
Therefore pf max = Distortion factor x displacement factor | max = 3/ π x cos α min = 0.85
p.f Min = 3/π x cos α max = 0.697
(iii) Power loss during charging = Io 2 RMS RB
But Io RMS 2 = Io 2 + I1 2 + I2 2 +………. And Ik ≈ VK / 6K wL = √ V 2 AK + V 2 BK / 6√2 K wL
For α = α min
VA1 = 0.439V VB1 = 48.8 V I1 = 0.073 Amps
VA2 = 10.76 VB2 = 20.15 I2 = 0.017 Amps
Jo 2 rms ≈ 100 2 +(0.073) 2 + (0.017) 2 = 10000.00562
Ploss = 100 watts.
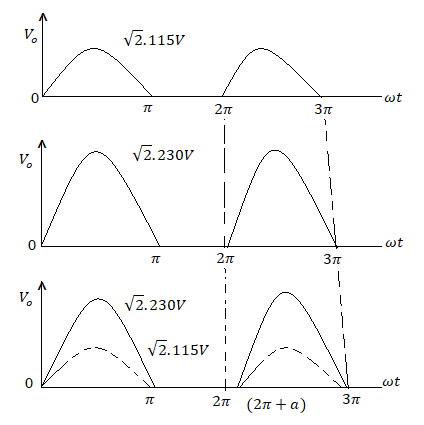
At α min Po = Io x Vb max 26400 watts
Charging effeiency = 26400/26400 + 100 = 99.6%
For αmax Io 2 rms = Io 2
Ploss = 100 watts
Po = Vo x Vb min = 21600 watts
Charging effeciency = 21600/ 21600 + 100 = 99.54 %
Q2) A three phase fully controlled converter operates from a 3 phase 230 V, 50 Hz supply through a Y/Δ transformer to supply a 220 V, 600 rpm, 500 A separately excited dc motor. The motor has an armature resistance of 0.02 Ω. What should be the transformer turns ratio such that the converter produces rated motor terminal voltage at 0º firing angle. Assume continuous conduction. The same converter is now used to brake the motor regeneratively in the reverse direction. If the thyristors are to be provided with a minimum turn off time of 100 μs, what is the maximum reverse speed at which rated braking torque can be produced.
A2) Form the above 3√2 / π VL = 220 V ; VL = 162.9V
Where VL is the secondary side line and also phase voltage since the secondary side is ∆ connected.
Primary side phase voltage = 230/√3 = 132.79V
Turns ratio = 132.79/162.9 = 1:1.2267
During regenrative braking in reverse direction the converter operates in the mode.
Tq| min = 100 µ sec
Β min = wtq| min = 1.8 0
Α max = 180 – β min = 178.2 0
The maximum negative voltage that can be generated by the converter is 3√2/π V L cos 178.2 = -219.89V
For rated braking torque Ia = 500 A
Eb = Va – Ia r = -229.89 V
At 600 RPM Eb= 220 – 500 x 0.02 = 210V
Maximum reverse speed is 229/210 x 600 = 656.83 RPM.
Q3) A three phase controlled rectifier has input voltage which is 480Vrms at 60Hz. The load is modelled as a series resistance and inductance with R = 10 Ω and L = 50mH. Determine the delay angle required to produce an average current of 50A in the load.
A3) Vdc = Idc . R = 50 x 10 = 500V
√ 3 Vrms = 480V
α= cos -1 Vdc π / 3 √3 Vm = cos -1 ( 500 π/ 3 √24 80) = 39.5 0
∴ Power factor = Displacement factor × Distortion factor =
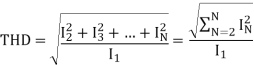
TUF
TUF=
Where
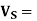 RMS supply (secondary) voltage
RMS supply (secondary) voltage
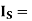 RMS supply (secondary) current
RMS supply (secondary) current
Q4) A single- phase full wave ac voltage controller working on ON-OFF control technique has supply voltage of 230V, RMS 50Hz, load = 50Ω. The controller is ON for 30 cycles and off for 40 cycles. Calculate
• ON & OFF time intervals.
• RMS output voltage.
• Input P.F.
• Average and RMS thyristor currents.
A4)
Vin(rms) = 230V; Vm = √ 2 x 230 = 325.269 V, Vm = 325.269 V
T = 1/f = 1/50 = 0.02 sec; T = 20 ms
n = number of input cycles during which controller is ON; n = 30
m = number of input cycles during which controller is OFF; m=40
TOn = n x T = 30 x 20 ms = 0.6 se
Controller ON time
TOFF = m x t = 40 x 20 ms = 800 msec = 0.8 sec
TOFF = controller OFF time.
Duty cycle k = n/ (m+n) = 30/40 + 30 = 0.4285
RMS output voltage:
Vo(rms) = Vi(rms) x √ n/(m+n)
= 230 x √ 30 / 30 + 40 = 230 √ 3/7 = 150.570V
Io(rms) = Vo(rms) / Z = Vo(rms) / RL = 150.570/50 = 3.0114A
Po = Io 2 (rms) x RL = 3.0114 2 x 50 = 453.426498W
Q5) A single phase voltage controller has input voltage of 230V, 50Hz and a load R=15 . For 6 cycles on and 4 cycles off determine (i) rms output voltage (ii) input pf (iii) Average and rms thyristor currents?
. For 6 cycles on and 4 cycles off determine (i) rms output voltage (ii) input pf (iii) Average and rms thyristor currents?
A5)
(a) rms value of output voltage is
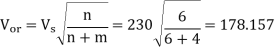
(b) input pf = 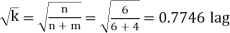
Also power delivered to load 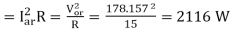
Input VA= 230×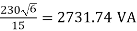
Input pf 
(c) Peak thyristor current 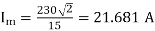
Average value of thyristor current
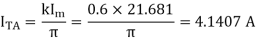
Rms value of thyristor current
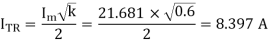
Q6) A single phase voltage controller feeds power to a resistive load of 3 from
(a) the maximum values of average and rms thyristor currents for any firing angle ,
(b) the minimum circuit turn-off time for any firing angle ,
(c) the ratio of third-harmonic voltage to fundamental voltage for 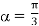
(d) the maximum value of di/dt occurring in the thyristors,
A6)
(a) It is seen current through thyristor flows from to π for the first cycle of 2π radians. Therefore, average thyristor current is given by
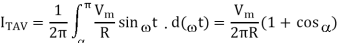
Its maximum value occurs when =0 therefore, maximum value of average thyristor current us
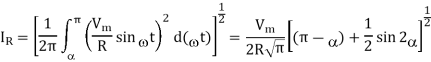
Its maximum value occurs at =0
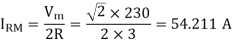
(b) Waveforms for  show that for any value of firing angle , the circuit turn-off time tis always π radians
show that for any value of firing angle , the circuit turn-off time tis always π radians
Circuit turn-off time 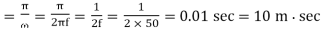
(c) For third harmonic 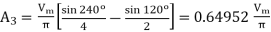

The amplitude of third harmonic voltage from eq(9.12) is 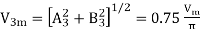
The amplitude of fundamental frequency from eq(9.15a)
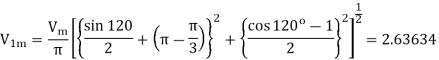
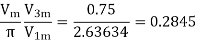
(d)
As there is a sudden rise of current from zero to  tat firing angle , di/dt is infinity.
tat firing angle , di/dt is infinity.
Q7) A single phase voltage controller is employed for controlling the power flow from 230 V, 50 Hz source into a load circuit consisting of R=3 and L=4 Calculate
(a) the control range of firing angle
(b) the control value of rms load current
(c) the maximum power and power factor
(d) the maximum values of average and rms thyristor currents
(e) the maximum possible value of di/dt that may occur in the thyristor and
(f) the conduction angle for =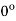 and
and 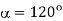 assuming a gate pulse of duration π radian.
assuming a gate pulse of duration π radian.
A7) (a) For controlling the load, the minimum value of firing angle =load phase angle 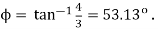 The maximum possible value of is
The maximum possible value of is 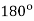 .
.
Firing angle control range is 
(b) the maximum value of rms load current  occurs when
occurs when 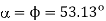 . But at thus value of firing angle, the power circuit of ac voltage controller behaves as if load is directly connected to ac source. Therefore maximum value of rms load current is
. But at thus value of firing angle, the power circuit of ac voltage controller behaves as if load is directly connected to ac source. Therefore maximum value of rms load current is
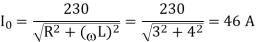
(c) Maximum Power 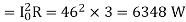
Power factor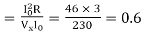
(d) Average thyristor current is maximum when 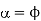 and conduction angle =π
and conduction angle =π
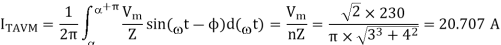
Similarly, maximum value of rms thyristor current is

(e)Maximum value of 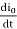 occurs when
occurs when 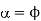

Its value s maximum when 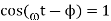
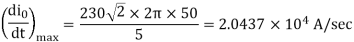
(f) For 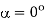 , that conduction angle is
, that conduction angle is  . For
. For 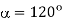 and
and  gives a conduction angle of about
gives a conduction angle of about 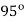 .
.
Q8) For the circuit shows in fig. (a) sketch the waveforms of output voltage
(a) sketch the waveforms of output voltage and current for the following values of firing angles.
(b) Only T2 is triggered at  etc
etc
(c) Only T1 is triggered at 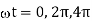 etc
etc
(c) T2 is triggered at t=0, 2π,4π etc. But T1 is triggered at 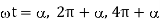 and so on. Take around
and so on. Take around 
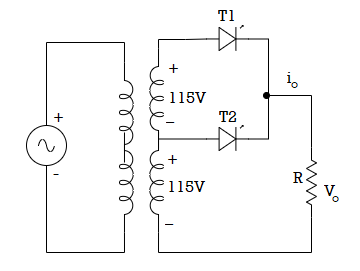
A8)
(a) At 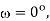 supply voltage is passing through zero and becoming positive. Therefore, when thyristor T2 turned off as load current
supply voltage is passing through zero and becoming positive. Therefore, when thyristor T2 turned off as load current 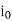 is zero. Load voltage
is zero. Load voltage 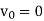 from
from  etc. as shown in
etc. as shown in  . For R load, current wave form is identical with voltage waveform.
. For R load, current wave form is identical with voltage waveform.
(b) This part is similar to part (a), except that the voltage amplitude is now  Fig (b-ii)
Fig (b-ii)
(c) At  etc. when T2 is triggered it gets turned on and
etc. when T2 is triggered it gets turned on and  At
At  etc. when forward biased thyristor T1 is triggered, it gets turned on. But when T1 gets on, a voltage equal to
etc. when forward biased thyristor T1 is triggered, it gets turned on. But when T1 gets on, a voltage equal to  appears as reverse bias across T2, it is therefore turned off at
appears as reverse bias across T2, it is therefore turned off at 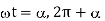 etc. Thus, from
etc. Thus, from 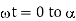 ,
, 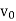 follows the curve
follows the curve  but from
but from 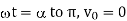 . From
. From 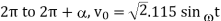 and from
and from 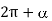 to
to 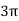 ,
, 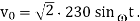 As the load is resistive, load current waveform is identical with load
As the load is resistive, load current waveform is identical with load 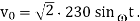 As the load is resistive, load current wave form is identical with load voltage waveform.
As the load is resistive, load current wave form is identical with load voltage waveform.
Input Power Factor 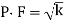
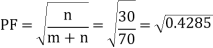
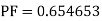
Average Thyristor Current Rating
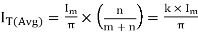
Where 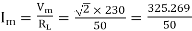
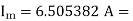 Peak (maximum) thyristor current
Peak (maximum) thyristor current
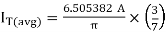
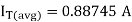
RMS Current Rating of Thyristor
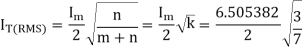
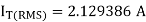
Q9) Draw the circuit and explain how three phase controlled convert can be analysed in the inverting mode?
A9) Analysis of the converter in the inverting mode.
In all the analysis it has been assumed that α < 90°. It is seen that the output dc voltage will be positive in this case and power will be flowing from the three- phase ac side to the dc side. This is the rectifier mode of operation of the converter.
However, if α is made larger than 90° the direction of power flow through the converter will reverse provided there exists a power source in the dc side of suitable polarity. The converter in that case is said to be operating in the inverter mode.
It has been explained in connection with single phase converters that the polarity of EMF source on the dc side would have to be reversed for inverter mode of operator.
Fig. Shows the circuit connection and wave forms in the inverting mode of operation where the load current has been assumed to be continuous and ripple free.
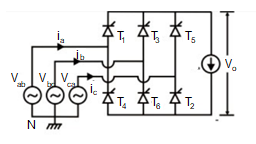
Figure. Inverting mode
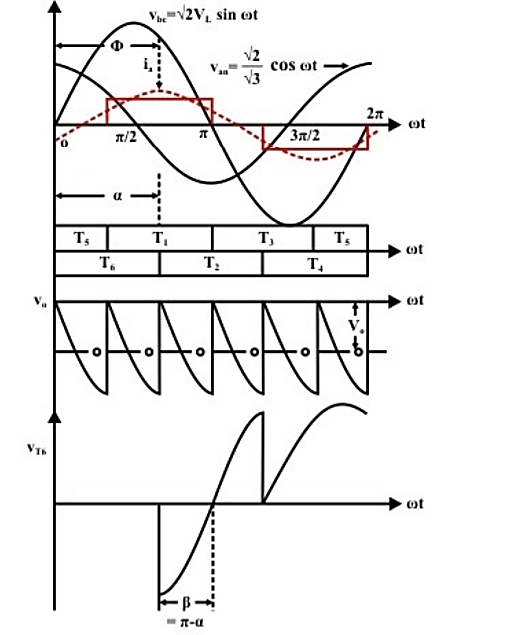
Fig. Wave forms in inverter mode of operation
Analysis of the converter in the inverting mode is similar to its rectifier mode of operation. The same expressions hold for the dc and harmonic compounds in the output voltage and current.
The input supply current Fourier series is

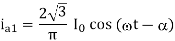
For values of α in the range 90° < α < 180° it is observed from Fig. 1(b) that the average dc voltage is negative and the displacement angle φ of the fundamental component of the input ac line current is equal to α > 90°.
Therefore, power in the ac side flows from the converter to the source. It is observed from Fig. 1(b) that an outgoing thyristor (thyristor T6 in Fig. 1(b)) after commutation is impressed with a negative voltage of duration β = π – α.
For successful commutation of the outgoing thyristor it is essential that this interval is larger than the turn off time of the thyristor i.e, β ω≥ tq , tq is the thyristor turn off time Therefore π - α ω≥ ≤ tq or α π -ωtq which imposes an upper limit on the value of α. In practice this upper value of α is further reduced due to commutation overlap.
Q10) Explain the operation of half controlled converter?
A10) Fig. (a) shows the circuit diagram of three phase half- controlled converter supplying an R-LE load. In the continuous conduction mode only one thyristor from top group and only one diode from the bottom group conduct at a time. However, unlike fully controlled converter here both devices from the same phase leg can conduct at the same time. Hence, there are nine conducting modes as shown in Fig. (b).

Figure. Half fully controlled three phase circuit and condution diagram
- Consider the conducting and blocking state of D2. In the blocking state the voltage across D2 is either Vac or Vbc. Hence, D2 can block only when these voltages are negative.
- Taking Vbc as the reference phasor (i.e., Vbc = 2V sinωt ) D2 will block during 2π/3 ≤ ωt ≤2π and will conduct in the interval 0 ≤ ωt ≤2π/3 .
- Similarly, it can be shown that D4 and D6 will conduct during 2π/3 ≤ ωt ≤ 4π/3 and 4π/3 ≤ ωt≤ 2π respectively. Next consider conduction of T1. The firing sequence of the thyristor is T1 → T3 → T5. Therefore, before T1 comes into conduction T5 conducts and voltage across T1 is Vac= 2V sin (ωt + π/3).
- If the firing angle of T1 is α then T1 starts conduction at ωt = α - π/3 and conducts up to α + π/3 . Similarly T3 and T5 conducts during α + π/3 ≤ ≤ ωt α + π and α + π ω≤ ≤t 2π + α - π/3.
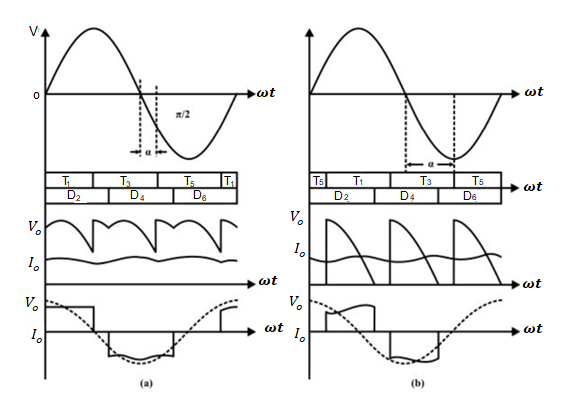
Figure. Waveforms of three half phase controller with α =  α =
α = 
Q11) In the 3-phase inverter circuit shown, the load is balanced and the gating scheme is 180c conduction mode. All the switching devices are ideal. (i) The rms value of load phase voltage. (ii) If the dc bus voltage Vd = 300, V the power consumed by 3-phase load?
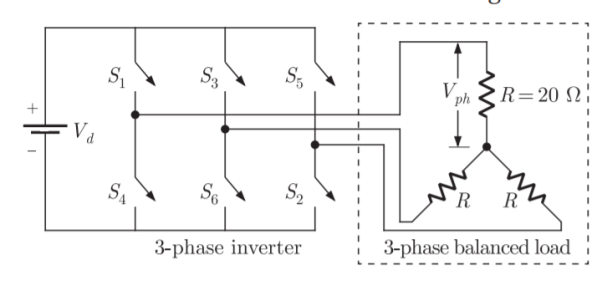
A11)
For a three-phase bridge inverter, rms value of output line voltage is
VL =√2/3 Vdc
Vdc = 300V
VL=141.4V
(ii) P=VL2/R = 3 x (141.4)2/20= 3kV
Q12) A solar energy installation utilize a three – phase bridge converter to feed energy into power system through a transformer of 400 V/400 V, as shown below. The energy is collected in a bank of 400 V battery and is connected to converter through a large filter choke of resistance 10 W. (i) The maximum current through the battery. (ii) The kVA rating of the input transformer?
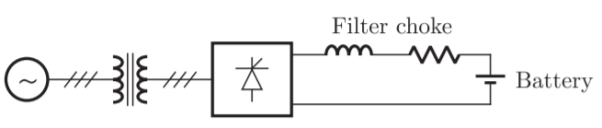
A12)
Output voltage of 3-phase bridge converter
Maximum output
Resistance of filter choke is 10 W, So
(V0)max = E + I Rchock
540.6 = 400 + I(10 )
I = 14 A
(ii) kVA Rating = √3 VL IL = √3 x 400 x(√6/π)x14 = 7.5kVA
Q13) The fully controlled thyristor converter in the figure is fed from a single-phase source. When the firing angle is 0c, the dc output voltage of the converter is 300 V. What will be the output voltage for a firing angle of 60c, assuming continuous conduction?
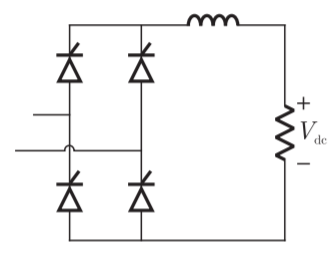
A13)
Given fully-controlled thyristor converter, when firing angle α = 0, dc output voltage Vdc0 = 300 V
If  then
then 
For fully-controlled converter
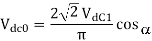
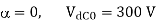
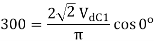

At  , then
, then 
For fully-controlled converter
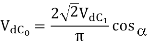
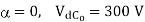
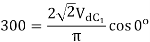
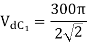
At 

Q14) In the single phase voltage controller circuit shown in the figure, for what range of triggering angle (α), the input voltage (V0) is not controllable?
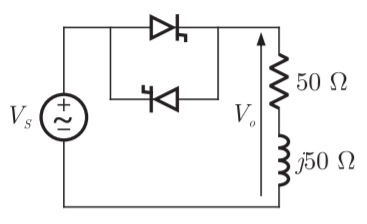

A14)
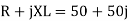

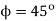
So firing angle ‘’ must be higher the 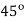 , thus for
, thus for 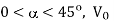 is uncontrollable.
is uncontrollable.
Q15) A single-phase half controlled converter shown in the figure feeding power to highly inductive load. The converter is operating at a firing angle of 600. If the firing pulses are suddenly removed, the steady state voltage (V0) waveform of the converter will be?
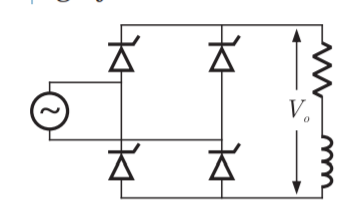
A15)
Here the inductor makes T1 and T3 in ON because current passing through T1 and T3 is more than the holding current.
Output of this will be
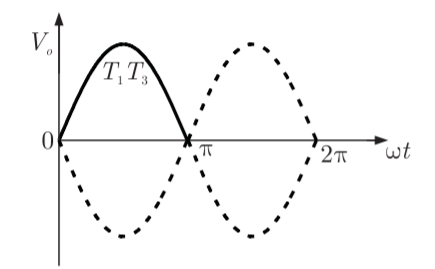
Q16) A single phase fully controlled converter bridge is used for electrical braking of a separately excited dc motor. The dc motor load is represented by an equivalent circuit as shown in the figure. Assume that the load inductance is sufficient to ensure continuous and ripple free load current. The firing angle of the bridge for a load current of I0 = 10 A will be?
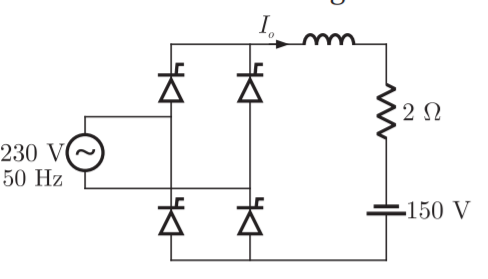
A16)
Here for continuous conduction mode, by Kirchoff’s voltage law, average load current
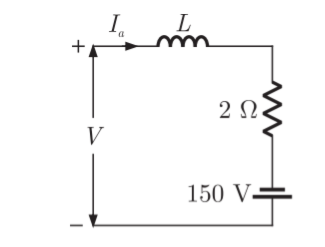
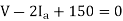
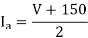
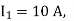 So
So
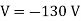
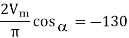
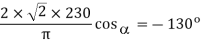
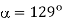
Q17) A three-phase, 440 V, 50 Hz ac mains fed thyristor bridge is feeding a 440 V dc, 15 kW, 1500 rpm separately excited dc motor with a ripple free continuous current in the dc link under all operating conditions, Neglecting the losses, the power factor of the ac mains at half the rated speed will be?
A17)
When losses are neglected,

Here back emf with  is constant
is constant
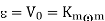
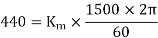
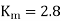
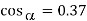
At this firing angle
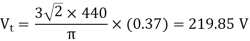
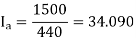

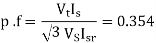
Q18) A 3-phase fully controlled bridge converter with free wheeling diode is fed from 400 V, 50 Hz AC source and is operating at a firing angle of 60c. The load current is assumed constant at 10 A due to high load inductance. The input displacement factor (IDF) and the input power factor (IPF) of the converter will be?
A18)
Given that
400 V, 50 Hz AC source, 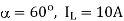
So,
Input displacement factor = cos =0.5
Input power factor =D.F ×cos
Distortion factor 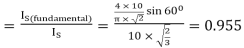
Input power factor =0.955 ×0.5=0.478
Q19) A solar cell of 350 V is feeding power to an ac supply of 440 V, 50 Hz through a 3-phase fully controlled bridge converter. A large inductance is connected in the dc circuit to maintain the dc current at 20 A. If the solar cell resistance is 0.5 W, then each thyristor will be reverse biased for a period of?
A19)
Let we have 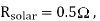
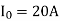
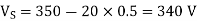
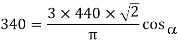

So each thyristor will reverse biased for 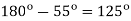
Q20) Consider a phase-controlled converter shown in the figure. The thyristor is fired at an angle α in every positive half cycle of the input voltage. If the peak value of the instantaneous output voltage equals 230 V, the firing angle a is close to?
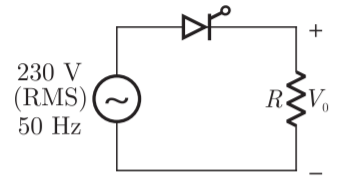
A20)
We know that 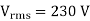
So, 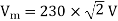
If whether 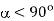
Then 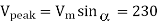
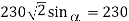
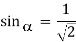
Angle