Question Bank

Unit 4

1. Explain random Sequences and Models of Convergence in Probability?

Convergence in probability is stronger than convergence in distribution. In particular, for a sequence X1, X2, X3, ⋯⋯ to converge to a random variable X, we must have that P(|Xn−X|≥ϵ) goes to 0 as n→∞ for any ϵ>0ϵ>0. To say that XnXn converges in probability to XX, we write

Xn→p X.

Here is the formal definition of convergence in probability:

Convergence in Probability

A sequence of random variables X1, X2, X3, ⋯⋯ converges in probability to a random variable X, shown by Xn→p X, if

Limn→∞P(|Xn−X|≥ϵ)=0, for all ϵ>0.

Problem:

Let X be a random variable, and Xn=X+Yn, where

EYn=1n,Var(Yn)=σ2n,where σ>0 is a constant. Show that Xn→p X.

Solution

First note that by the triangle inequality, for all a,b∈R, we have

|a+b|≤|a|+|b|.

Choosing a=Yn−EYn and b=EYn, we obtain

|Yn|≤|Yn−EYn|+1n.

Now, for any ϵ>0, we have

P(|Xn−X|≥ϵ)

=P(|Yn|≥ϵ)≤P(|Yn−EYn|+1/n≥ϵ)

=P(|Yn−EYn|≥ϵ−1/n)≤Var(Yn)/(ϵ−1/n)2

=σ2n(ϵ−1/n)2→0 as n→∞.(by Chebyshev's inequality)

Therefore, we conclude Xn→p X.

2.Explain random Sequences and Models of Convergence in Probability?

If we define the distance between Xn and X as P(|Xn−X|≥ϵ), we have convergence in probability. One way to define the distance between Xn and X is E(|Xn−X|r),

Where r≥1 is a fixed number. This refers to convergence in mean. The most common choice is r=2, in which case it is called the mean-square convergence.

Convergence in Mean

Let r≥1 be a fixed number. A sequence of random variables X1, X2, X3, ⋯ converges in the rth mean or in the Lr norm to a random variable X, shown by Xn−→Lr X, if

Lim n→∞ E(|Xn−X|r)=0.

If r=2, it is called the mean-square convergence, and it is shown by Xn→m.s. X.

3.Consider a sequence {Xn,n=1,2,3,⋯} such that

Xn = {   n 2                   with probability 1/n

                0                     with probability 1-1/n     

Show thatXn→p 0.

Xn does not converge in the rth mean for any r≥1.

Solution

To show Xn→p 0, we can write, for any ϵ>0

Limn→∞P(|Xn|≥ϵ)

=limn→∞P(Xn=n2)

=limn→∞1/n=0.

We conclude that Xn→p 0.

For any r≥1, we can write

Limn→∞E(|Xn|r) =limn→∞(n2r⋅1/n+0⋅(1−1/n))

=limn→∞n2r−1=∞(since r≥1).

Therefore, Xn does not converge in the rth mean for any r≥1. In particular, it is interesting to note that, although Xn→p 0, the expected value of Xn does not converge to 0.

4.Explain Strong law of large numbers

Let X1, X2, X3, ⋯ be a sequence of i.i.d. Uniform(0,1) random variables. Define the sequence Yn as

Yn=min(X1,X2,⋯,Xn).

Prove the following convergence results independently (i.e, do not conclude the weaker convergence modes from the stronger ones).

Yn →d 0.

Solution

Yn →d 0:

Note that

FXn(x) = { 0                  x<0

                    x                 0 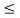x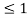

1                                   x

Note that RYn = [0,1] for 0 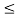y we can write

F Yn (y) = P ( Yn 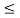y)

                   1 – P( Yn > y)

                    1 – P (X1 >y, X2>y, ………………Xn >y)

                    1 – P (X1>y) P(X2>y) ……………P(Xn>y)

                  = 1 – ( 1 – Fx1(y))(1-Fx2(y))…..(1 – FXn(y))

          = 1 – (1-y) n

Therefore we conclude that

Lim FYs(y) = { 0               y 0

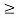1                               y   0

Therefore Yn ->d0

5. Explain weak law of large numbers?

Weak Law of large numbers

The weak law of large numbers (WLLN)

Let X1, X2 , ... , Xn be i.i.d. Random variables with a finite expected value EXi=μ<∞. Then, for any ϵ>0,

Limn→∞P(|X¯−μ|≥ϵ)=0.

The proof of the weak law of large number is easier if we assume Var(X)=σ2 is finite. In this case we can use Chebyshev's inequality to write

P(|X¯−μ|≥ϵ)

=Var(X)n/ϵ2,

≤Var(X¯)/ϵ2

Which goes to zero as n→∞.

6. Explain Central limit theorem?

The central limit theorem (CLT) is one of the most important results in probability theory.

It states that, under certain conditions, the sum of a large number of random variables is approximately normal.

Here, we state a version of the CLT that applies to i.i.d. Random variables. Suppose that X1, X2 , ... , Xn are i.i.d. Random variables with expected values EXi=μ<∞ and variance Var(Xi)=σ2<∞. Then the sample mean X¯¯=X1+X2+...+Xnn has mean EX¯=μ and variance Var(X¯)=σ2n. Thus, the normalized random variable.

Zn=X¯−μσ/n−=X1+X2+...+Xn−nμn−√σ

Has mean EZn=0 and variance Var(Zn)=1. The central limit theorem states that the CDF of Zn converges to the standard normal CDF.

Let X1,X2,...,Xn be i.i.d. Random variables with expected value EXi=μ<∞ and variance 0<Var(Xi)=σ2<∞. Then, the random variable

Zn=X¯−μ/σ/ √n=X1+X2+...+Xn−nμ/ 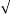nσ

Converges in distribution to the standard normal random variable as n goes to infinity, that is

Limn→∞P(Zn≤x)=Φ(x), for all x∈R,

Where Φ(x) is the standard normal CDF.

7. What are the steps to apply central limit theorem?

Here are the steps that we need in order to apply the CLT:

1.Write the random variable of interest, Y, as the sum of n i.i.d. Random variable Xi's:

Y=X1+X2+...+Xn.

2.Find EY and Var(Y) by noting that

EY=nμ,Var(Y)=nσ2,

Where μ=EXi and σ2=Var(Xi).

3.According to the CLT, conclude that

Y−EY/ √Var(Y)=Y−nμ/ √nσ is approximately standard normal; thus, to find P(y1≤Y≤y2), we can write

P(y1≤Y≤y2)=P(y1−nμ/√nσ≤Y−nμ/√nσ≤y2−nμ/√nσ)

≈Φ(y2−nμ/ √nσ)−Φ(y1−nμ/√nσ).

8. In a communication system each data packet consists of 1000 bits. Due to the noise, each bit may be received in error with probability 0.1. It is assumed bit errors occur independently. Find the probability that there are more than 120 errors in a certain data packet.

Solution

Let us define Xi as the indicator random variable for the ith bit in the packet. That is, Xi=1 if the ith bit is received in error, and Xi=0 otherwise. Then the Xi's are i.i.d. And Xi∼Bernoulli(p=0.1).

If Y is the total number of bit errors in the packet, we have

Y=X1+X2+...+Xn.

Since Xi∼Bernoulli(p=0.1), we have

EXi=μ=p=0.1,Var(Xi)=σ2=p(1−p)=0.09

Using the CLT, we have

P(Y>120)=P(Y−nμ/ √nσ>120−nμ/√nσ)

=P(Y−nμ/√nσ>120−100/ √90)

≈1−Φ(20/√90)=0.0175

Continuity Correction:

Let us assume that Y∼Binomial(n=20,p=12), and suppose that we are interested in P(8≤Y≤10). We know that a Binomial(n=20,p=12) can be written as the sum of n i.i.d. Bernoulli(p) random variables:

Y=X1+X2+...+Xn.

Since Xi∼Bernoulli(p=12), we have

EXi=μ=p=12,Var(Xi)=σ2=p(1−p)=14.

Thus, we may want to apply the CLT to write

P(8≤Y≤10)=P(8−nμ/√nσ<Y−nμ/√nσ<10−nμ/ √nσ)

=P(8−10/√5 <Y−nμ/ √nσ<10−10/ √5)≈Φ(0)−Φ(−2/√5)=0.3145

Since, here, n=20 is relatively small, we can actually find P(8≤Y≤10) accurately. We have

P(8≤Y≤10)=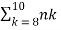pk(1−p)n−k

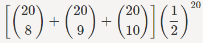
=0.4565

We notice that our approximation is not so good. Part of the error is due to the fact that Y is a discrete random variable and we are using a continuous distribution to find P(8≤Y≤10). Here is a trick to get a better approximation, called continuity correction. Since Y can only take integer values, we can write

P(8≤Y≤10)

=P(7.5<Y<10.5)

=P(7.5−nμ/√nσ<Y−nμ/√nσ<10.5−nμ/√nσ)

=P(7.5−10/√5 <Y−nμ/√nσ<10.5−10/√5)

≈Φ(0.5/√5)−Φ(−2.5/√5)

=0.4567

As we see, using continuity correction, our approximation improved significantly. The continuity correction is particularly useful when we would like to find P(y1≤Y≤y2), where Y is binomial and y1 and y2 are close to each other.  

9. Explain the applications of central limit theorem?

10. Explain the advantages of central limit theorem?

The Central Limit Theorem is important for statistics because it allows us to safely assume that the sampling distribution of the mean will be normal in most cases. This means that we can take advantage of statistical techniques that assume a normal distribution.