Unit - 2

Decision Tree Learning

Q1) What are some Learning algorithms used in Inductive Bias?

A1)

Inductive Bias are -

Q2) Write a short note on the Hypothesis space?

A2)

The Hypothesis space H is the set of all possible models h which can be learned by the current learning algorithm – e.g. Set of possible weight settings for a perceptron

Restricted hypothesis space –

• Can be easier to search
• May avoid overfitting since they are usually simpler (e.g. Linear or low order decision surface)
• Often will underfit l Unrestricted Hypothesis Space
• Can represent any possible function and thus can fit the training set well
• Mechanisms must be used to avoid overfitting

Distinct Observations in X = 3.2.2.2.2.2 = 96

Distinct hypothesis in H = 5.4.4.4.4.4 = 5120

Q3) What is an Unbiased Learner?

A3)

An Unbiased Learner can be explained as through this figure the box on the left represents the set X of all instances, the box on the right the set H of all hypotheses. Each hypothesis corresponds to some subset of X.

Suppose if we have 3 instances then we can have pow(2,3) = 8 subsets. Each subset corresponds to one hypothesis in the hypothesis space. Each hypothesis will learn a concept that is represented by the subset of the instances. By having such a hypothesis space will represent every teachable concept that is representing every possible subset of the instances X.

Note — out of 8 hypotheses, only 1 hypothesis is a conjunctive and the rest 7 hypothesis are disjunctions, conjunctions, and negations combinations.

In the Enjoy Sport learning task, the size of the instance space X of days described by the six attributes is (3.2.2.2.2.2 = ) 96 instances. In total, we can have pow (2,96) subsets from the 96 district instances.

The solution to the problem of assuring that the target concept is in the hypothesis space H is to provide a hypothesis space capable of representing every teachable concept that is representing every possible subset of the instances X.

The set of all subsets of a set X is called the power set of X.

Note, the conjunctive hypothesis space can represent only (4.3.3.3.3.3 =) 973 of these — a biased hypothesis space indeed.

Let us reformulate the Enjoy sports learning task in an unbiased way by defining a new hypothesis space H’ that can represent every subset of instances; that is, let H’ correspond to the power set of X. One way to define such an H’ is to allow arbitrary disjunctions, conjunctions, and negations of our earlier hypotheses.

For instance, the target concept “Sky = Sunny or Sky = Cloudy” could then be described as (Sunny, ?, ?, ?, ?, ?) v (Cloudy, ?, ?, ?, ?, ?).

However, while this hypothesis space eliminates any problems of expressibility, it, unfortunately, raises a new, equally difficult problem: our concept learning algorithm is now completely unable to generalize beyond the observed examples.

Q4) Explain the fundamental property of inductive inference.

A4)

“A learner that makes no a priori assumptions regarding the identity of the target concept has no rational basis for classifying any unseen instances”

The only reason that the candidate elimination algorithm was able to generalize beyond the observed training examples in our original formulation of the Enjoy Sport task is that it was biased by the implicit assumption that the target concept could be represented by a conjunction of attribute values. In cases where this assumption is correct (and the training examples are error-free), its classification of new instances will also be correct. If this assumption is incorrect, however, the candidate elimination algorithm will certainly miss-classify at least some instances from X.

Q5) Write a short note on Inductive Bias for Candidate Elimination

A5) Algorithm for Inductive Bias for Candidate Elimination

• Assume a training set Dc. The candidate elimination algorithm computes the version space VS_HD.
• Classify the new instance xi by a vote among hypotheses in this version space. Here let us assume that it will output a classification for xi only if this vote among version space hypotheses is unanimously positive or negative and that it will not output a classification otherwise
• Conjecture: B = { c ∈ H } is the inductive bias (’the underlying target concept c is in H’) From c ∈ H it follows that c is a member of the version space.
• L (xi, Dc) = k implies that all members of VS_HD, including c, vote for class k (unanimous voting). Therefore: c(xi) = k = L( xi, Dc ).
• This means, that the output of the learner L(xi, Dc) can be logically deduced from B ∧ Dc ∧ xi
• → The inductive bias of the Candidate Elimination Algorithm is: “c is in H”

Q6) Elaborate Reduced Error Pruning?

A6)

Reduced Error Pruning is an approach,(Quinlan 1987), is used in the validation set to prevent overfitting and is to consider each of the decision nodes in the tree to be candidates for pruning.

• Reduced-error pruning is to consider each of the decision nodes in the tree to be candidates for pruning
• Pruning a decision node consists of removing the subtree rooted at that node, making it a leaf node, and assigning it the most common classification of the training examples affiliated with that node
• Nodes are removed only if the resulting pruned tree performs no worse than-the original over the validation set.
• Reduced error pruning affects that any leaf node added due to coincidental regularities in the training set is likely to be pruned because these same coincidences are unlikely to occur in the validation set

Q7) Explain with an example of Concept Learning Task

A7)  

Enjoy Sport Concept Learning Task

Define the learning task for Enjoy Sport Concept.

1. X — The set of items over which the concept is defined is called the set of instances, which we denote by X. In the current example, X is the set of all possible days, each represented by the attributes Sky, AirTemp, Humidity, Wind, Water, and Forecast.
2. c — The concept or function to be learned is called the target concept, which we denote by c. In general, c can be any boolean-valued function defined over the instances X; that is, c: X → {0, 1}.

In this current example, the target concept corresponds to the value of the attribute EnjoySport (i.e, c(x)=1 if EnjoySport=Yes, and c(x)=0 if EnjoySport= No)

3.     (x, c(x)) — When learning the target concept, the learner is presented with a set of training examples, each consisting of an instance x from X, along with its target concept value c(x). Instances for which c(x) = 1 are called positive examples and instances for which c(x) = 0 are called negative examples. We will often write the ordered pair (x, c(x)) to describe the training example consisting of the instance x and its target concept value c(x).

4.     D — We use the symbol D to denote the set of available training examples.

5.     H — Given a set of training examples of the target concept c, the problem faced by the learner is to hypothesize, or estimate, c. We use the symbol H to denote the set of all possible hypotheses that the learner may consider regarding the identity of the target concept.

6.     h(x) — In general, each hypothesis h in H represents a Boolean-valued function defined over X; that is, h: X →{0, 1}.

The goal of the learner is to find a hypothesis h such that h(x) = c(x) for all x in X.

Algorithm for Enjoy Sport Concept Learning Task

Given

-         Instances X: set of all possible days, each described by the attributes

• Sky – (values: Sunny, Cloudy, Rainy)
• AirTemp – (values: Warm, Cold)
• Humidity – (values: Normal, High)
• Wind – (values: Strong, Weak)
• Water – (values: Warm, Cold)
• Forecast – (values: Same, Change)

-         Target Concept (Function) c: EnjoySport: X → {0, 1}

-         Hypotheses H: Each hypothesis is described by a conjunction of constraints on the attributes.

-         Training Examples D: positive and negative examples of the target function

Determine

-         A hypothesis h in H such that h(x) = c(x) for all x in D.

Q8) Explain some basic features of an artificial neuron.

A8)  

A neuron is a mathematical function modeled on the working of biological neurons

• It is an elementary unit in an artificial neural network
• One or more inputs are separately weighted
• Inputs are summed and passed through a nonlinear function to produce output
• Every neuron holds an internal state called activation signal
• Each connection link carries information about the input signal
• Every neuron is connected to another neuron via a connection link

Q9) What is a Perceptron Function?

A9)

Perceptron is a function that maps its input “x,” which is multiplied with the learned weight coefficient; an output value ”f(x)” is generated.

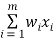
In the equation given above:

“w” = vector of real-valued weights

“b” = bias (an element that adjusts the boundary away from the origin without any dependence on the input value)

“x” = vector of input x values

“m” = number of inputs to the Perceptron

The output can be represented as “1” or “0.”  It can also be represented as “1” or “-1” depending on which activation function is used.

Q10) Write the Principle of Gradient Descent.

A10)

Gradient descent is an optimization algorithm that approaches a local minimum of a function by taking steps proportional to the negative of the gradient of the function as the current point.