Unit - 3

Evaluating Hypotheses

Q1) What is Evaluation Hypothesis?

A1) Estimating Hypotheses Accuracy

This is made clear by distinguishing between the true error of a model and the estimated or sample error. One is the error rate of the hypothesis over the sample of data that is available. The other is the error rate of the hypothesis over the entire unknown distribution D of examples.

Machine learning, specifically supervised learning, can be described as the desire to use available data to learn a function that best maps inputs to outputs.

Technically, this is a problem called function approximation, where we are approximating an unknown target function (that we assume exists) that can best map inputs to outputs on all possible observations from the problem domain.

An example of a model that approximates the target function and performs mappings of inputs to outputs is called a hypothesis in machine learning.

The choice of algorithm (e.g. Neural network) and the configuration of the algorithm (e.g. Network topology and hyperparameters) define the space of possible hypotheses that the model may represent.

Q2) Define the process of Sampling.

A2) Process of Sampling:

1. Identifying the Population set.
2. Determination of the size of our sample set.
3. Providing a medium for the basis of selection of samples from the Population medium.
4. Picking out samples from the medium using one of many Sampling techniques like Simple Random, Systematic, or Stratified Sampling.
5. Checking whether the formed sample set contains elements that match the different attributes of the population set, without large variations in between.
6. Checking for errors or inaccurate estimations in the formed sample set, that may or may not have occurred
7. The set which we get after performing the above steps contributes to the Sample Set.

Q3) State the differences between Supervised and Unsupervised learning.

A3) The main differences between Supervised and Unsupervised learning are given below.

Q4) State Bayes’s theorem.

A4) Bayes' Theorem:

Bayes' theorem is also known as Bayes' Rule or Bayes' law, which is used to determine the probability of a hypothesis with prior knowledge. It depends on the conditional probability.

The formula for Bayes' theorem is given as:

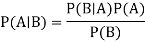
 Where,

P(A|B) is Posterior probability: Probability of hypothesis A on the observed event B.

P(B|A) is Likelihood probability: Probability of the evidence given that the probability of a hypothesis is true.

P(A) is Prior Probability: Probability of hypothesis before observing the evidence.

P(B) is a Marginal Probability: Probability of Evidence.

Q5) State types of Naïve Bayes Model.

A5) There are three types of Naive Bayes Model, which are given below:

Gaussian: The Gaussian model assumes that features follow a normal distribution. This means if predictors take continuous values instead of discrete, then the model assumes that these values are sampled from the Gaussian distribution.

Multinomial: The Multinomial Naïve Bayes classifier is used when the data is multinomial distributed. It is primarily used for document classification problems, it means a particular document belongs to which category such as Sports, Politics, education, etc. The classifier uses the frequency of words for the predictors.

Bernoulli: The Bernoulli classifier works similarly to the Multinomial classifier, but the predictor variables are the independent Booleans variables. Such as if a particular word is present or not in a document. This model is also famous for document classification tasks.

Q6) Define the advantages and disadvantages of EM algorithms.

A6) Advantages of EM algorithm –

1. It is always guaranteed that likelihood will increase with each iteration.
2. The E-step and M-step are often pretty easy for many problems in terms of implementation.
3. Solutions to the M-steps often exist in the closed-form.

Disadvantages of EM algorithm –

1. It has slow convergence.
2. It makes convergence to the local optima only.
3. It requires both the probabilities, forward and backward (numerical optimization requires only forward probability).

Q7) Write a short note on types of Naive Bayes Classifier

A7) Types of Naive Bayes Classifier

Multinomial Naive Bayes:

This is mostly used for the document classification problem, i.e whether a document belongs to the category of sports, politics, technology, etc. The features/predictors used by the classifier are the frequency of the words present in the document.

Bernoulli Naive Bayes:

This is similar to the multinomial naive Bayes but the predictors are boolean variables. The parameters that we use to predict the class variable take up only values yes or no, for example, if a word occurs in the text or not.

Gaussian Naive Bayes:

When the predictors take up a continuous value and are not discrete, we assume that these values are sampled from a gaussian distribution.

Gaussian distribution (Normal Distribution)

Since the way the values are present in the dataset changes, the formula for conditional probability changes to,

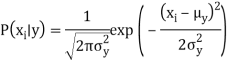
Naive Bayes algorithms are mostly used in sentiment analysis, spam filtering, and recommendation systems, etc. They are fast and easy to implement but their biggest disadvantage is that the requirement of predictors to be independent. In most real-life cases, the predictors are dependent, this hinders the performance of the classifier.

Q8) Write a short note on the Bayesian method.

A8) Bayesian methods provide the basis for probabilistic learning methods that accommodate (and require) knowledge about the prior probabilities of alternative hypotheses and about the probability of observing various data given the hypothesis. Bayesian methods allow assigning a posterior probability to each candidate hypothesis, based on these assumed priors and the observed data. 0 Bayesian methods can be used to determine the most probable hypothesis given the data-the maximum a posteriori (MAP) hypothesis. This is the optimal hypothesis in the sense that no other hypothesis is more likely.

The Bayes optimal classifier combines the predictions of all alternative hypotheses, weighted by their posterior probabilities, to calculate the most probable classification of each new instance.

Q9) Write the significance of naive Bayes classifier.

A9) The naive Bayes classifier is a Bayesian learning method that is useful in many practical applications. It is called "naive" because it incorporates the simplifying assumption that attribute values are conditionally independent, given the classification of the instance. When this assumption is met, the naive Bayes classifier outputs the MAP classification. Even when this assumption is not met, as in the case of learning to classify text, the naive Bayes classifier is often quite effective. Bayesian belief networks provide a more expressive representation for sets of conditional independence assumptions among subsets of the attributes.

The framework of Bayesian reasoning can provide a useful basis for analyzing certain learning methods that do not directly apply the Bayes theorem. For example, under certain conditions, it can be shown that minimizing the squared error when learning a real-valued target function corresponds to computing the maximum likelihood hypothesis.

The Minimum Description Length principle recommends choosing the hypothesis that minimizes the description length of the hypothesis plus the description length of the data given the hypothesis. Bayes's theorem and basic results from information theory can be used to provide a rationale for this principle.

Q10) What is a Bayesian Belief Network?

A10) A Bayesian belief network describes the probability distribution governing a set of variables by specifying a set of conditional independence assumptions along with a set of conditional probabilities. In contrast to the naive Bayes classifier, which assumes that all the variables are conditionally independent given the value of the target variable, Bayesian belief networks allow stating conditional independence assumptions that apply to subsets of the variables. Thus, Bayesian belief networks provide an intermediate approach that is less constraining than the global assumption of conditional independence made by the naive Bayes classifier, but more tractable than avoiding conditional independence assumptions altogether. Bayesian belief networks are an active focus of current research, and a variety of algorithms have been proposed for learning them and for using them for inference