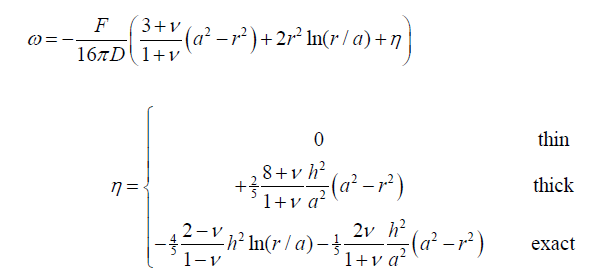UNIT 5

Introduction to Theory of Plates and Shells

Q1) Discuss assumptions of Classical Plate theory (KCPT)

A1) Assumptions-

Thickness is smaller than the other dimension.

Displacements are much smaller than plate thickness.

Governing equations are based on unreformed geometry.

Materials follow Hook’s Law.

The middle surface is always unstrained during bending.

The Plane normal to the middle surface remains normal.

Rotatory inertia is negligible. Transverse shear strains also negligible.

Q2) Explain Higher-order Shear Deformation Beam Theories?

A2) To deal with ambiguity in deciding suitable shear coefficients in case of first-order shear deformation theories, the interest is later switched over to higher-order shear deformation theories. In case of higher-order shear deformation theories, the displacement field of the theories can predict realistic transverse shear stress distribution through the beam height. Also, the displacement field can satisfy zero shear stress surface conditions. Hence, the need for using shear coefficients in the beam formulation can be avoided.

Q3) Explain Boundaries conditions?

A3) Boundary Conditions:

There are three possibilities of boundary condition-

1. Simply supported-

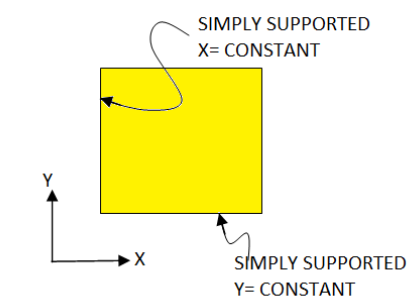
Figure - Middle plane

For x constant –

w( x , y ) = 0

For edge y constant-

W=0

2. Clamped-

For x constant –

W=0

For y constant-

W=0

Q4) What is plate?

A4) Plates

A plate is a flat structural element for which the thickness is small compared with the surface dimensions. The thickness is usually constant but may be variable and is measured normal to the middle surface of the plate, Fig. 6.1.1

Q5) Discuss From Beam Theory to Plate Theory?

A5) In the beam theory, based on the assumptions of plane sections remaining plane and that one can neglect the transverse strain, the strain varies linearly through the thickness.

In the notation of the beam, with y positive up 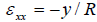, where R is the radius of curvature, R positive when the beam bends “up”. In terms of the curvature 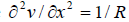where v is the deflection, one has

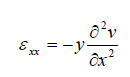
The beam theory assumptions are essentially the same for the plate, leading to strains which are proportional to distance from the neutral (mid-plane) surface, z, and expressions similar to 6.2.1. This leads again to linearly varying stresses 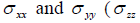is also taken to be zero, as in the beam theory).

Q6) Explain Curvature and Twist?

A6) The plate is initially undeformed and flat with the mid-surface lying in the x - y plane.

When deformed, the mid-surface occupies the surface w = w(x, y) and w is the elevation above the x - y plane, Fig. 6.2.1.

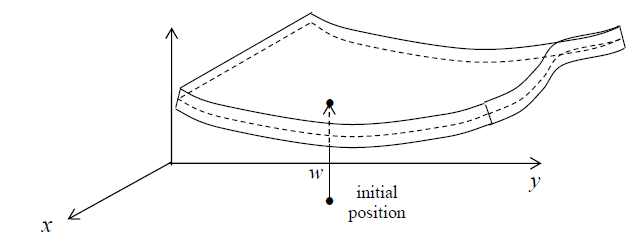
Fig: Deformed Plate

The slopes of the plate along the x and y directions are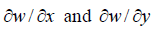

Q7) What is Von Karman Strains?

A7) Introduce now the assumptions of the classical plate theory. The assumption that line elements normal to the mid-plane remain inextensible implies that

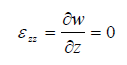
This implies that w =w(x, y) so that all particles at a given (x, y) through the thickness of the plate experience the same vertical displacement. The assumption that line elements Perpendicular to the mid-plane remain normal to the mid-plane after deformation then imply that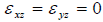 

The strains now read

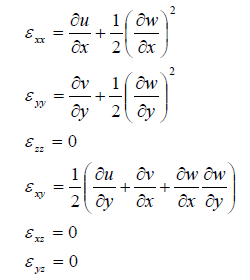
These are known as the Von Karman strains

Q8) Explain stresses and the Curvatures/Twist in a Linear Elastic Plate?

A8) From Hooke’s law, taking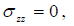

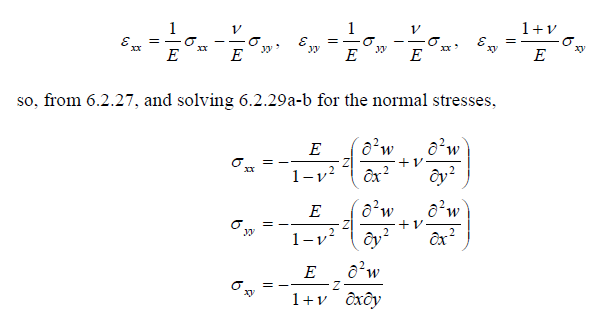
Q9) Write limitations of Classical Plate Theory?

A9) The validity of the classical plate theory depends on a number of factors:

1. The curvatures are small

2. The in-plane plate dimensions are large compared to the thickness

3. Membrane strains can be neglected

Q10) Explain Comparison of solution for circular plates?

A10) Comparison of Solutions for Circular Plates

1. Uniform load q, clamped:

Both thin and thick plate theories give

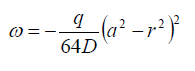
2. Uniform load q, simply supported

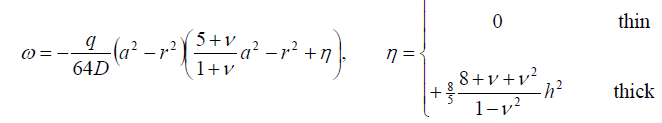
3. Concentrated central load, clamped (Eqn. 6.6.25):

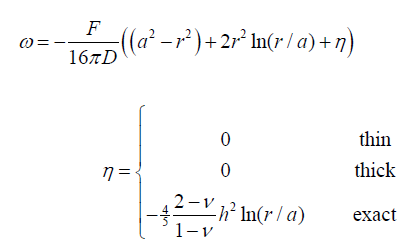
4. Concentrated central load Q, simply supported: