UNIT-1
Introduction to solid, liquid and gaseous fuels
Question 1: What is fuel? Explain its different types.
A1): Fuel is a substance which, when consumed on coming in contact and responding with Oxygen or air produces heat. Along these lines the substances delegated fuel should essentially contain one or a few of the burnable components carbon, hydrogen, sulphur, and so on during the time spent burning, the substance energy of fuel is changed over into heat energy.
To use the energy of fuel in most usable structure, it is needed to change the fuel from its one state to another, for example from strong to fluid or vaporous state, fluid to vaporous state, or from its compound energy to some other type of energy through single or numerous stages. Along these lines, the energy of powers can be used all the more viably and proficiently for different purposes.
1. Solid fuel
Strong energizes are predominantly grouped into two classes, for example characteristic energizes, for example, wood, coal, and so forth and produced powers, for example, charcoal, coke, briquettes, and so on
2. Liquid fuel
These are the powers which are found in fluid state and simpler to deal with and use when contrasted with strong powers. The normally accessible fluid fuel is oil which isn't utilized straightforwardly as it is combination of various helpful substances. Along these lines prior to utilizing, it is refined by bubbling and build-up measure in processing plants refineries to isolate into various helpful substances like petroleum, lamp oil, fuel oils, greasing up oils, coal tar and so on Out of these some are utilized as powers, yet some like greasing up oil, coal tar are utilized in different applications, From our subject perspective the accompanying fluid energizes are significant.
3. Gaseous fuels
These are additionally normally accessible or misleadingly arranged. The flammable gas is accessible under the world's surface close to oil fields. It is a combination of methane, ethane and other like gases. Vaporous energizes are should have been packed for putting away in compartments and furthermore for powerful use. They are hard to deal with and require huge hefty compartments however their bit of leeway is that they promptly burst into flames and liberated from contaminations. So ignition is finished and furthermore contamination is less.
Question 2: Explain Ash zone, ignition zone, reduction zone, distillation zone.
A2):
Ash Zone
The least zone comprises of for the most part of debris, and along these lines, it is known as debris zone.
Ignition Zone
The zone close to the debris zone is known as oxidation or ignition zone. Here the carbon consumes and shapes CO and CO2. The temperature of this zone is about 1100oC. The accompanying responses happen.
C+O2=CO2 + 94 Kcal
C + ½ O2 = CO + 29.5 kcal
Reduction Zone
Here carbon dioxide and steam consolidates with super-hot carbon and Frees free hydrogen and carbon monoxide. The responses are:
CO2 + C = 2CO – 94 kcal
C + H2O = CO + H2 + 29 kcal
C + 2H2O = CO2 + 2H2 – 19 kcal
All these decrease responses are endothermic, thus, the temperature in the decrease zone tumbles to 1000oC.
Distillation zone
In this zone (400 – 800oC) the approaching coal is warmed by active gases by giving reasonable warmth to the coal. The warmth given by the gases and warmth transmitted from the decrease zone serves to distillate the fuel consequently unpredictable matter of coal is added to the active gas.
Question 3: Explain the advantages and disadvantages of gaseous fuels.
A3): Advantages
Gaseous fuels due to erase and flexibility of their applications possess the Following advantages over solid or liquid fuels:
(a) They can be passed on effectively through pipelines to the real spot of Need accordingly dispensing with difficult work in transportation.
(b) They can be lit calm.
(c) They have high warmth substance and consequently help us in having higher temperatures.
(d) They can be pre-warmed by the warmth of hot waste gases, in this way influencing economy in warmth.
(e) Their ignition can promptly by controlled for change popular like oxidizing or decreasing air, length fire, temperature, and so on
(f) They are spotless being used.
(g) They don't need any extraordinary burner.
(h) They consume with no shoot, or smoke and cinders.
(I) They are liberated from pollutions found in strong and fluid fills.
Disadvantages
(a) Extremely enormous capacity tanks are required.
(b) They are exceptionally inflammable, so odds of fire risks in their utilization are high.
Question 4: Explain the exhaust gas analysis.
A4): The essential ignition cycle can be depicted by the fuel (the hydrocarbon) in addition to oxidizer (air or oxygen) called the Reactants, which go through a chemical process while delivering heat to form the product of combustion such that mass is conserved.
In the least complex burning cycle, known as Stoichiometric combustion, all the carbon in the fuel structures carbon dioxide (CO2) and all the hydrogen structures water (H2O) in the items, in this manner we can compose the chemical reaction as follows:
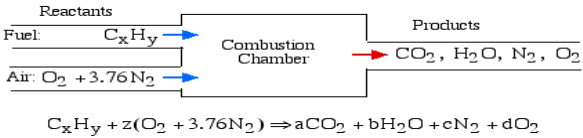
Where z is known as the stoichiometric coefficient for the oxidizer (air) Note that this response yields five questions: z, a, b, c, d, subsequently we need five conditions to tackle. Stoichiometric burning accepts that no abundance oxygen exists in the items, consequently d = 0. We get the other four conditions from adjusting the quantity of particles of every component in the reactants (carbon, hydrogen, oxygen and nitrogen) with the quantity of atoms of those components in the items. This implies that no molecules are demolished or lost in a burning response.
Element | Amount in reactants | = | Amount in Products | Reduced equation |
Carbon (C) | X |
| a | a = x |
Hydrogen (H) | Y |
| 2b | b = y/2 |
Oxygen (O) | 2z |
| 2a+b | z = a + b/2 |
Nitrogen (N) | 2(3.76)z |
| 2c | c = 3.76z |
Question 5: What is first law of analysis of combustion.
A5): The First Law Analysis of Combustion:
The fundamental motivation behind ignition is to deliver heat through a difference in enthalpy from the reactants to the items. From the first Law condition in a control volume, ignoring kinetic and potential energy changes and expecting no work is done, we have:
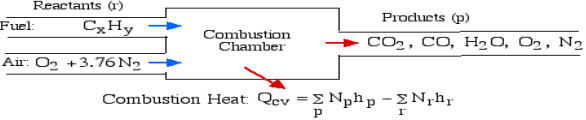
Where the summations are assumed control over all the items (p) and the reactants (r). N alludes to the quantity of moles of every part and h [kJ/kmol] alludes to the molar enthalpy of every segment.
For example, rethink the total ignition of Methane (CH4) with hypothetical air:
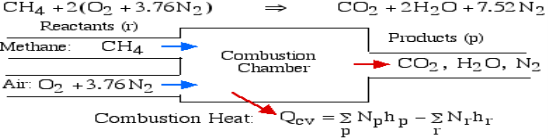
Notice that in the reactants and the results of the above model we have essential components O2 and N2 just as mixes CH4, CO2, and H2O. At the point when the compound is shaped then the enthalpy change is known as the Enthalpy of Development, signified hfo, and for our model:
Substance | Formula | hfo [kJ/kmol] |
Carbon dioxide | CO2(g) | -393,520 |
Water Vapor | H2O(g) | -241,820 |
Water | H2O(l) | -285,820 |
Methane | CH4(g) | -74,850 |
Where (g) alludes to gas and (l) alludes to fluid. The negative sign implies that the cycle is Exothermic, for example heat is radiated when the compound is framed. Note that the enthalpy of development of fundamental components O2 and N2 is zero.
Consider first the case in which there is adequate heat transfer such that both the reactants and the items are at 25°C and 1 atom pressure, and that the water item is fluid. Since there is no reasonable enthalpy change the energy condition becomes:
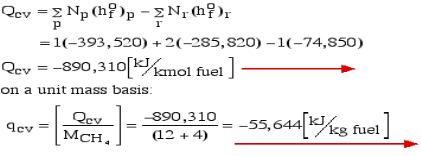
Question 6: Define Enthalpy.
The precise definition of enthalpy (H) is the sum of the internal energy (U) plus the product of pressure (P) and volume (V). In symbols, this is:
H = U + PV
A change in enthalpy (∆H) is therefore:
∆H = ∆U + ∆P∆V
Where the delta symbol (∆) means “change in.” In practice, the pressure is held constant and the above equation is better shown as:
∆H = ∆U + P∆V
However, for a constant pressure, the change in enthalpy is simply the heat (q) transferred:
∆H = q
If (q) is positive, the reaction is endothermic (i.e., absorbs heat from its surroundings), and if it is negative, the reaction is exothermic (i.e., releases heat into its surroundings). Enthalpy has units of kJ/mol or J/mol, or in general, energy/mass. The equations above are really related to the physics of heat flow and energy: thermodynamics.
Question 7: Explain Simple Enthalpy Change Calculation:
A7): The most basic way to calculate enthalpy change uses the enthalpy of the products and the reactants. If you know these quantities, use the following formula to work out the overall change:
∆H = Hproducts − Hreactants
The addition of a sodium ion to a chloride ion to form sodium chloride is an example of a reaction you can calculate this way. Ionic sodium has an enthalpy of −239.7 kJ/mol, and chloride ion has enthalpy −167.4 kJ/mol.
Sodium chloride (table salt) has an enthalpy of −411 kJ/mol. Inserting these values gives:
∆H = −411 kJ/mol – (−239.7 kJ/mol −167.4 kJ/mol)
= −411 kJ/mol – (−407.1 kJ/mol)
= −411 kJ/mol + 407.1 kJ/mol = −3.9 kJ/mol
So the formation of salt releases almost 4 kJ of energy per mole.
Question 8: Define adiabatic flame temperature.
A8): At the point when a combustion reaction takes place energy is delivered to the ignition items. On the off chance that no heat is lost in this cycle, the temperature of the burning items is known as the "Adiabatic Fire Temperature.
For an combustion cycle that happens adiabatically with no shaft work, the temperature of the items is alluded to as the adiabatic fire temperature. This is the greatest temperature that can be accomplished for given reactants. heat transfer, incomplete combustion, and separation all outcome in lower temperature. The most extreme adiabatic flame temperature for a given fuel and oxidizer mix happens with a stoichiometric combination (right extents to such an extent that all fuel and all oxidizer are burned-through). The measure of abundance air can be custom fitted as a component of the plan to control the adiabatic fire temperature. The significant distance between present temperatures in a gas turbine engine and the most extreme adiabatic flame temperature at stoichiometric conditions compressor exit temperature of 12000F (922 K).
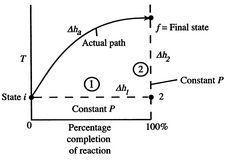
Figure 1: Schematic of adiabatic flame temperature
An initial perspective on the idea of adiabatic flame temperature is given by inspecting two responding gases, at a given pressing factor, and asking what the end temperature is. The cycle is indicated schematically in Figure 1, where temperature is plotted versus the percentage completion of the reaction. The underlying state is i and the last state is f with the final state at a higher temperature than the initial state. The strong line in the figure shows a portrayal of the ''actual'' process.
Question 9: Derive the expression for Adiabatic flame temperature.
A9): To perceive how we would show up at the final completion state the dashed lines break the condition of reaction change into two sections. Process (1) is reaction at consistent T and P. To complete such a cycle, we would have to extract heat. Assume the aggregate sum of heat extraction per unit mass is q1. The connection between the enthalpy changes in process (1) is
h2- h1= -q1= (hof) unit mass
Where q1is the heat of reaction.''
For Process (2), we put this amount back into the products to raise their temperature to the final level. For this process,
hf – h2 = q1
Or if we can approximate the specific heat as constant (using some appropriate average value).
CP.avg(Tf – T2) = q1
For the overall process there is no work done and no heat exchanged so that the difference in enthalpy between initial and final states is zero:
∆h1 + ∆h2 = ∆Hadiabatic = 0
The temperature change during this second process is therefore given by (approximately).
(Tf – T2) = q1 / Cp.avg = (hof) unit mass / Cp.avg
The estimation of the adiabatic flame temperature given in Condition (15.5) is for 100% finish of the reaction. In reality, as the temperature increases, the tendency is for the degree of reaction to be less than 100%. For example, for the burning of hydrogen and oxygen, at high temperatures the combustion product (water) separates once more into the less difficult basic reactants. The degree of reaction is in this manner itself a component of temperature that need to be computed. We utilized this thought in discussing the stoichiometric ramjet, when we said that the greatest temperature was autonomous of flight Mach number and subsequently of inlet stagnation temperature. It is also to be emphasized that the idea of a constant (average) specific heat, Cp average is for illustration and not inherently part of the definition of adiabatic flame temperature.
A model calculation of adiabatic flame temperature is furnished by the combustion of liquid octane at with 400% hypothetical air. The response is
C8H18(l) + 12.3 O2 + 12.5(3.76N2) + 3[12.5O2 + 12.5(3.76N2)] → 8CO2 + 9H2O(g) + 37.5O2 + 188N2
For an adiabatic process
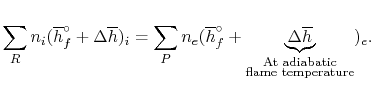
We can again think of the general process in steps:
1. Bring reactants to 250C [the term(∆h)i ] from the initial temperature, using whatever heat transfer, qa is required. In this model we needn't bother with step (i) since we are now at the reference temperature.
2. Reaction at 250c [the term(hof) reactants-products]. There will be some heat transfer in this progression, qb out of the combustor.
3. Put back warmth qa+qb into the results of ignition. The subsequent temperature is the adiabatic flame temperature.
In the present case
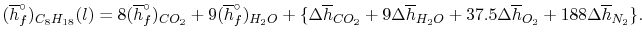
We can look at the terms in the SFEE independently, beginning with the heat of formation terms, and monitoring units:
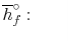
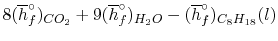
= 8 k mole (-393,522 kJ /k mole) + 9 k mole (-241,827 kJ/k mole)
= - 1 k mole (-249,952 KJ/k mole)
= - 5.075 X 106 kJ
The exit state at the adiabatic flame temperature is determined by:
We find the adiabatic flame temperature in three ways:
An approximate solution using an average value of Cp
A more precise one utilizing the organized development of Cp with temperature,
Question 10: What is chemical equilibrium and calculation of it using free energy.
A10): We have identified three criteria for whether a given reaction will occur spontaneously: ΔSuniv > 0, ΔGsys < 0, and the relative magnitude of the reaction quotient Q versus the equilibrium constant K. Recall that if Q < K, then the reaction proceeds spontaneously to the right as written, resulting in the net conversion of reactants to products. Conversely, if Q > K, then the reaction proceeds spontaneously to the left as written, resulting in the net conversion of products to reactants. If Q = K, then the system is at equilibrium, and no net reaction occurs. Table 1 summarizes these criteria and their relative values for spontaneous, nonspontaneous, and equilibrium processes.
Table Criteria for the Spontaneity of a Process | ||
Spontaneous | Equilibrium | Nonspontaneous* |
*Spontaneous in the reverse direction. | ||
ΔSuniv > 0 | ΔSuniv = 0 | ΔSuniv < 0 |
ΔGsys < 0 | ΔGsys = 0 | ΔGsys > 0 |
Q < K | Q = K |
|
Because all three criteria are assessing the same thing—the spontaneity of the process—it would be most surprising indeed if they were not related. In this section, we explore the relationship between the standard free energy of reaction (ΔG°) and the equilibrium constant (K).
Because ΔH° and ΔS° determine the magnitude of ΔG° and because K is a measure of the ratio of the concentrations of products to the concentrations of reactants, we should be able to express K in terms of ΔG° and vice versa. "Free Energy", ΔG is equal to the maximum amount of work a system can perform on its surroundings while undergoing a spontaneous change. For a reversible process that does not involve external work, we can express the change in free energy in terms of volume, pressure, entropy, and temperature, thereby eliminating ΔH from the equation for ΔG. The general relationship can be shown as follow
ΔG=VΔP-SΔT…..1
If a reaction is carried out at constant temperature (ΔT = 0), then Equation 1 simplifies to
ΔG=VΔP…..2
Under normal conditions, the pressure dependence of free energy is not important for solids and liquids because of their small molar volumes. For reactions that involve gases, however, the effect of pressure on free energy is very important.
Assuming ideal gas behaviour, we can replace the V in Equation 2 by nRT/P (where n is the number of moles of gas and R is the ideal gas constant) and express ΔGin terms of the initial and final pressures (Pi and Pf , respectively):
ΔG = (nRT / P) ΔP = n RT (ΔP / P) = n RT in (Pf / Pi)……3
If the initial state is the standard state with Pi = 1atm then the change in free energy of a substance when going from the standard state to any other state with a pressure P can be written as follows:
G−G°=nRTlnP…….4
This can be rearranged as follows:
G=G°+nRTlnP…..5
As you will soon discover, Equation 5allows us to relate ΔG° and Kp. Any relationship that is true for Kp must also be true for K because Kp and K are simply different ways of expressing the equilibrium constant using different units.
Let’s consider the following hypothetical reaction, in which all the reactants and the products are ideal gases and the lowercase letters correspond to the stoichiometric coefficients for the various species:
aA+bB⇌cC+dD……..6
Because the free-energy change for a reaction is the difference between the sum of the free energies of the products and the reactants, we can write the following expression for ΔG:
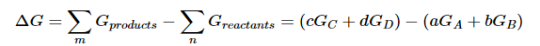 ……7
……7
Substituting Equation 5 for each term into Equation 7,
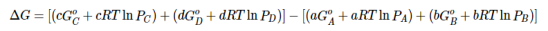 ….8
….8
Combining terms gives the following relationship between ΔG and the reaction quotient Q:
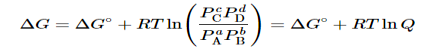 …..9
…..9
Where ΔG° indicates that all reactants and products are in their standard states. For gases at equilibrium (Q=KpQ=Kp), and as you’ve learned in this chapter, ΔG = 0 for a system at equilibrium. Therefore, we can describe the relationship between ΔG° and Kp for gases as follows:
0=ΔG°+RTlnKp……10
ΔG°=−RTlnKp……...11