Unit - 4

Digital Electronics Fundamentals

Q1) Write the Difference between analog and digital signals?

A1)

Q2) Give a short note on Boolean algebra.

A2)

Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra. Boolean algebra was invented by George Boole in 1854.

Rule in Boolean Algebra

Following are the important rules used in Boolean algebra.

• Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
• Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as 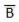. Thus if B = 0 then  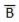= 1 and B = 1 then  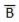= 0.
• ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.
• Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.

Q3) Write a description on Basic and Universal Gates?

A3)

        The basic gates are namely AND gate, OR gate & NOT gate.

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

                                         Fig. : AND gate (ref. 1)

Timing Diagram:

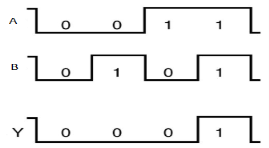
OR gate

It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of 2-input OR gate is:

Here A, B are the inputs and Y is the output of two input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

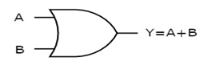
Fig. : OR gate (ref. 1)

Timing Diagram:

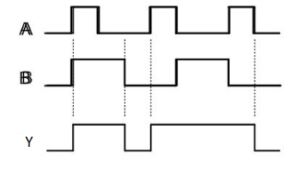
NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

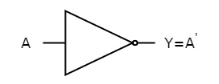
                                             Fig. : NOT gate (ref. 1)

Timing Diagram:

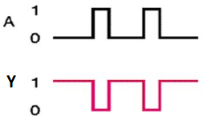
Universal gates

      NAND & NOR gates are known as universal gates.

      We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of 2-input NAND gate is:

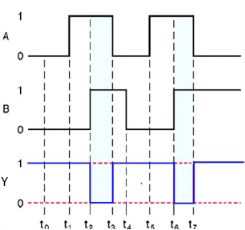
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

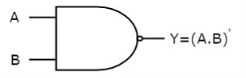
                                              Fig.: NAND gate (ref. 1)

NAND gate works same as AND gate followed by an inverter.

Timing Diagram:

NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the input is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.

The symbol of NOR gate is:

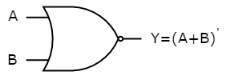
                                                           Fig.: NOR gate (ref. 1)

NOR gate works exactly same as that of OR gate followed by an inverter.

Timing Diagram:

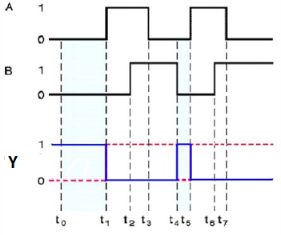
Special Gates

Ex-OR gate

It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

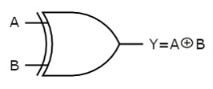
                                                           Fig.: XOR gate (ref. 1)

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

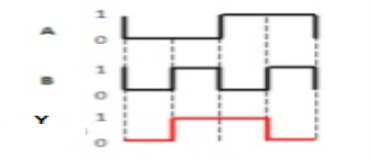
Ex-NOR gate

It stands for Exclusive-NOR gate. Its function is same as that of NOR gate except when the inputs having even number of ones.

The truth table of 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.

Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.

The symbol of Ex-NOR gate is:

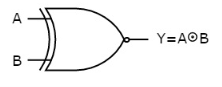
                                       Fig.: XNOR gate (ref. 1)

It is similar to NOR gate except for few combination(s) of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.

Timing Diagram:

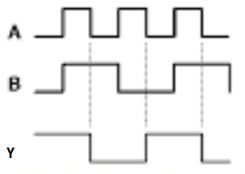
Q4) Short note on Logic IC’s.

A4)

1.        7400 Quad 2 input NAND gates
2. 7402 Quad 2 input NOR gates
3. 7404 Hex NOT gates (Inverters)
4. 7408 Quad 2 input AND gates
5. 7432 Quad 2 input OR gates
6. 7486 Quad 2 input XOR gates
7. 747266 Quad 2 input XNOR gates
8. 74133 Single 13 input NAND gate

Q5) What do you understand by Half and full adder?

A5)

           is a combinational circuit which has two inputs and two outputs.

      It is designed to add two single bit binary number A and B.

      It has two outputs carry and sum.

Block diagram

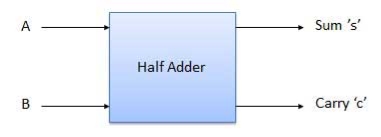
                                  Fig. : Half adder (ref. 2)

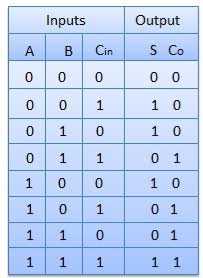
Truth Table

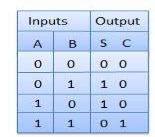
Circuit Diagram

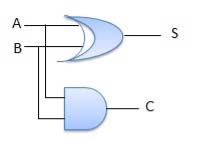
                             Fig.: Half adder (ref. 2)

Full Adder

      It is developed to overcome the drawback of Half Adder circuit.

      It can add two one-bit numbers A and B and a carry C.

      It is a three input and two output combinational circuit.

Block diagram

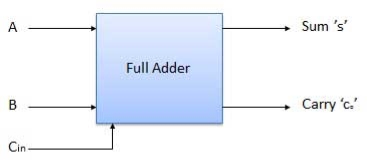
                             Fig. : Full adder (ref. 2)

Circuit Diagram

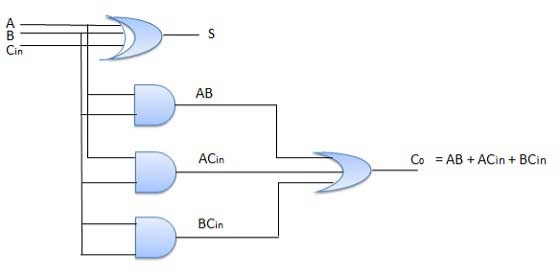
                             Fig. : Full adder (ref. 2)

Q6) Explain the work of Multiplexers?

A6)

•     It is a special type of combinational circuit.
• It has n-data inputs, one output and m inputs select lines with 2m = n.
• It selects one of the n data inputs and routes it to the output.
• The selection of one of the inputs is done by the select lines.
• Depending on the code applied at the inputs, one of the n data sources is selected and transmitted to the single output Y.
• E is the enable input which is useful for cascading purpose.
• It is an active low terminal hence performs the required operation when it is low.

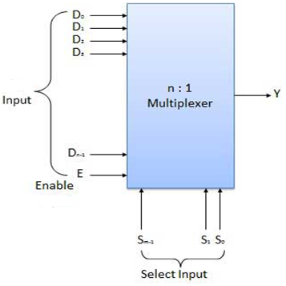
Fig.: Block diagram of multiplexer (ref. 2)

Multiplexers come in multiple variations

• 2 : 1 multiplexer
• 4 : 1 multiplexer
• 16 : 1 multiplexer
• 32 : 1 multiplexer

Block Diagram of 2:1 MUX

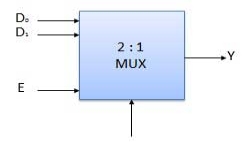
Truth Table of 2:1 MUX

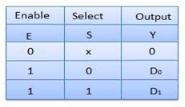
Where x is don’t care.

Q7) Explain the function of De-multiplexers?

A7)

•   It performs the inverse operation of a multiplexer as it receives one input and distributes it across its outputs.
• It has only one input and n outputs with m select input.
• At a time only one output line is selected by the select lines and that input is transmitted through the output line.
• It is equivalent to a single pole multiple way switch .

Various Demultiplexers are used as:

• 1 : 2 demultiplexer
• 1 : 4 demultiplexer
• 1 : 16 demultiplexer
• 1 : 32 demultiplexer

Block diagram

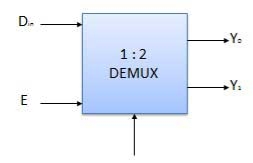
Truth Table

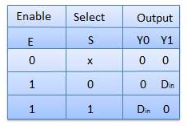
Where x is don’t care.

Q8) What do you understand by Flip-flops?

A8)
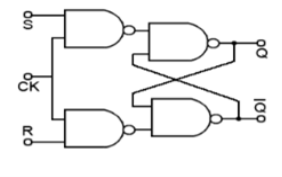
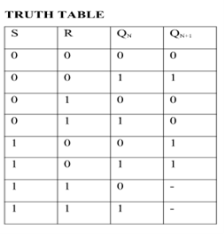
SR Flip Flop

JK Flip Flop

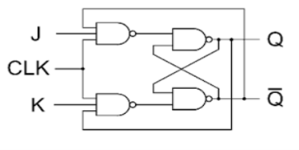
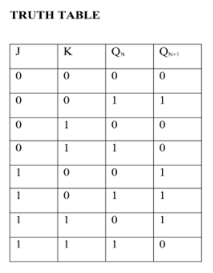
Race Around Condition In JK Flip-flop –

• For J-K flip-flop, if J=K=1, and if clk=1 for a long period of time, then output Q will toggle as long as CLK remains high which makes the output unstable or uncertain.
• This problem is known as race around condition in J-K flip-flop.
• This problem can be avoided by ensuring that the clock input is at logic “1” only for a very short time.
• Hence the concept of Master Slave JK flip flop was introduced.

D Flip Flop

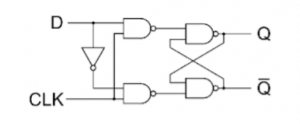
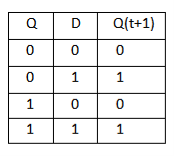
T Flip Flop

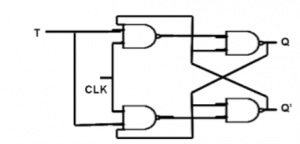
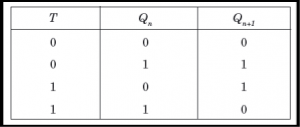
Q9) Give a short note on Shift registers.

A9)

• Flip flops are used to store one bit of binary data (1or 0).
• If we need to store multiple bits of data, we use multiple flip flops.
• N flip flops are connected to store n bits of data.
• A Register is a device which stores such information. It is a group of flip flops connected in series which is used to store multiple bits of data.
• The information stored in these registers can be transferred with the help of shift registers.
• This register is a group of flip flops used to store multiple bits of data.
• The bits stored in these registers can be moved in/out of the registers by applying clock pulses.
• The registers which shift the bits towards left are called “Shift left registers”.
  The registers which shift the bits towards right are called “Shift right registers”.

Shift registers are of 4 types and they are:

1. Serial In Serial Out register
2. Serial In parallel Out register
3. Parallel In Serial Out register
4. Parallel In parallel Out register

Serial-In Serial-Out Shift Register (SISO) –

• It allows serial input i.e. one bit after another and produces a serial output is known as Serial-In Serial-Out shift register.
• Since it has one output, the data leaves the register one bit at a time in a serial pattern, hence known as Serial-In Serial-Out Shift Register.
• The logic circuit is given underneath.
• The circuit comprises of four D flip-flops which are connected serially.
• All these flip-flops are synchronous in nature

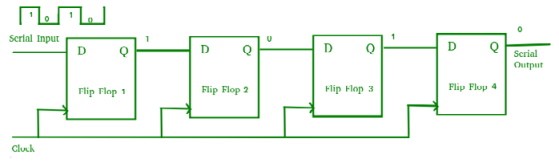
                                                         Fig.  SISO

Serial-In Parallel-Out shift Register (SIPO) –

• It allows serial input through a single data line and produces a parallel output.
• The logic circuit is given underneath .
• The circuit consists of four D flip-flops which are connected synchronously.
• The clear (CLR) signal is also connected to all the 4 flip flops in order to RESET them.
• The output of the first flip flop is sent to the input of the next and so on.

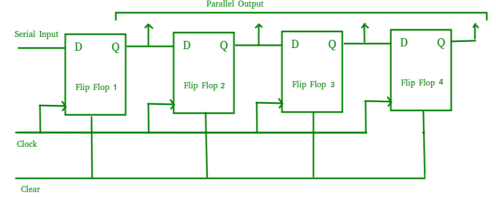
                                                         Fig.  SIPO

• They are used in communication lines because the main use of the SIPO register is to convert serial data into parallel data.

Parallel-In Serial-Out Shift Register (PISO) –

• It allows parallel input data and produces a serial output.
• The logic circuit is given underneath.
• The circuit comprises of four D flip-flops which are connected synchronously.
• The clock is connected to all the flip flops but the input data is connected to each flip flop individually through a multiplexer .
• The output of the previous flip flop and parallel data input are connected to the input of the MUX and the output of MUX is connected to the next flip flop.

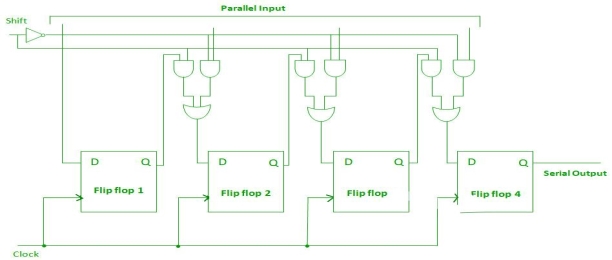
                                                         Fig.  PISO

• It used to convert parallel data to serial data.

Parallel-In Parallel-Out Shift Register (PIPO) –

• It allows parallel input data and produces a parallel output.
• The logic circuit is given underneath.
• The circuit comprises of four D flip-flops which are connected in a synchronous manner.
• The clear (CLR) and clock signals are connected to all flip flops.
• In this, there are no interconnections between flip-flops as no serial shifting of the data is required.
• Data is provided separately as input for each flip flop and the output is also collected individually from each flip flop.

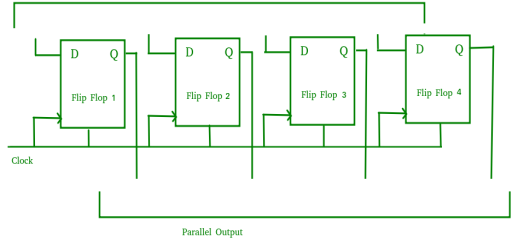
                                                         Fig. PIPO

• It is used as a temporary storage device and it acts as a delay element too.

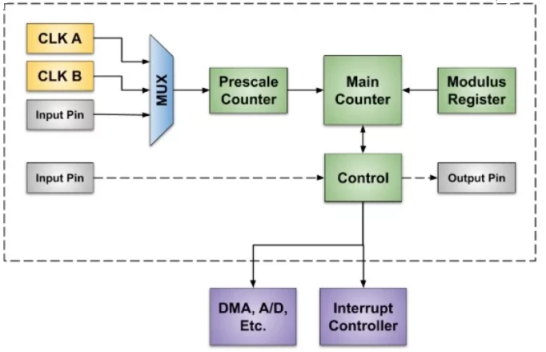
Q10) Write in brief about the function of Counters?

A10)

      A Counter stores the number of times a particular event or process has occurred in relationship to a clock signal. 

      They are used in digital electronics for counting purpose.

      They can count specific event happening how many times in the circuit.

      For example, in UP counter count increases for every rising edge of clock.

      A counter can follow certain sequence based on our design like any sequence 0,1,3,2… .

      They can be designed with the help of flip flops.

Counter Classification

Counters are broadly classified into two categories:

1. Asynchronous counter
2. Synchronous counter

1. Asynchronous Counter

      In this universal clock is not used and only the first flip flop is driven by main clock and the clock input of rest of the following is driven by output of previous flip flops.

                                         Fig.  Asynchronous counter

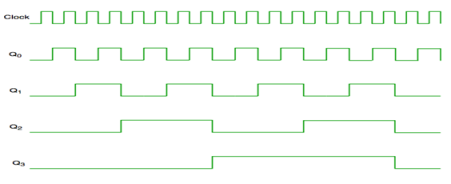
                                        Fig.  Timing diagram of Asynchronous counter

      It is seen from timing diagram that Q0 is changing as soon as the rising edge of clock pulse is encountered.

      Q1 is changing when rising edge of Q0 is encountered and so on.

      In this way ripples are generated through Q0,Q1,Q2,Q3  and therefore  it is also called  as a RIPPLE counter.

2. Synchronous Counter

      It has one global clock which drives each and every flip flop and hence output changes in parallel.

      The advantage of synchronous counter over asynchronous counter is that it can operate on higher frequency and  it does not have cumulative delay .

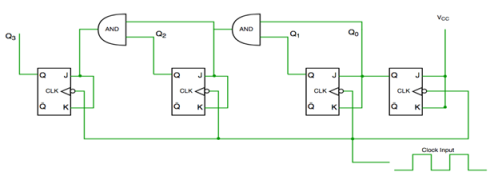
                                                   Fig.  synchronous counter

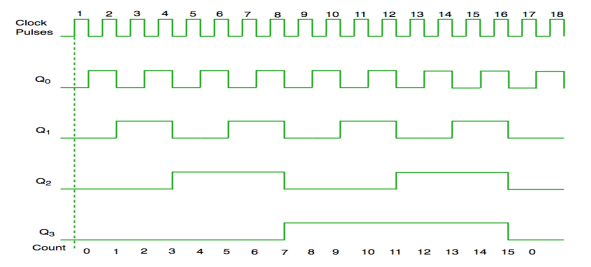
                                                Fig.  Timing diagram of synchronous counter

Q11) What do you understand by microprocessor/microcontroller and explain its application?

A11)

  Microprocessor: Introduction

• It is a controlling unit that is fabricated on a small chip.
• It is capable to perform arithmetic logic operations and communicate with various devices connected to it.
• It comprises of an ALU (Arithmetic Logic Unit), MU (Memory unit) and CU (Control unit).
• It also consists of register array with registers named as B, C, D, E, H, L and ACC.

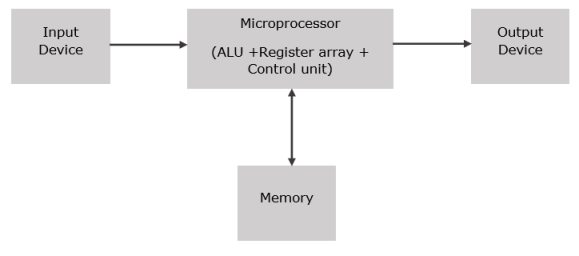
                                Fig.: Basic block diagram of microprocessor

Microcontroller: Introduction

• Microcontroller is a compact tiny computer that is fabricated inside a chip and is used in automatic control systems including security systems, office machines, power tools, alarming system, traffic light control, washing machine, and much more.
• It is economical programmable logic control that can be interfaced with external devices in order to control the devices from a distance.
• It was specially built for embedded system and consisted of read write memory, read only memory, I/O ports, processor and built in clock.
• C and assembly languages are used to program the microcontrollers.
• There are also other languages available to program the microcontroller but at the start learning a microcontroller programming with C and assembly language is a great choice, both are easy to learn and provide a clear concept about microcontroller.
• Technology have been evolved in an amazing way and made our lives easier more than ever before.