undefined | unit 5 properties of areas

Engineering Mechanics

Unit 5

Properties of Areas

Q1. An airplane A is traveling northeast with a speed of 160 m/s A second airplane B is traveling southeast with a speed of 200 m/s. Find a vector expression that expresses the velocity of aircraft A as seen from an observer flying in aircraft B. Calculate this vector. What is its magnitude and direction?

Solution:

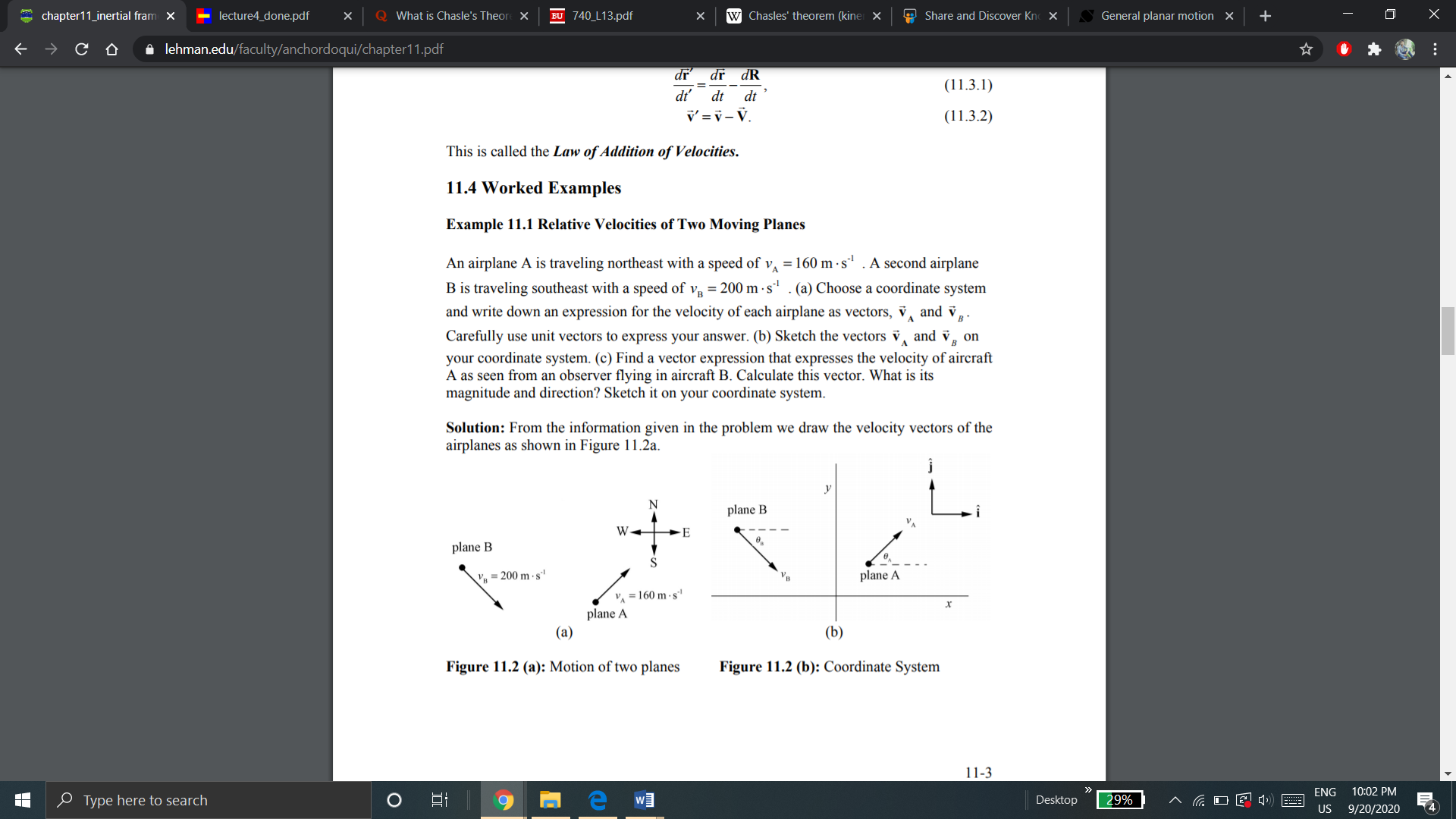
A flies northeast so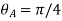

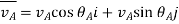
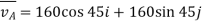
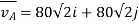
B flies southeast so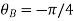

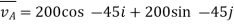
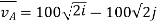
The velocity of airplane A with respect to an observer moving along with Airplane B is given by

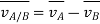
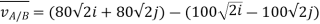
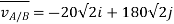
Magnitude is given by

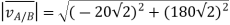
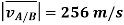
Direction is given by

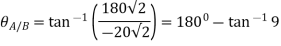
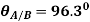
Q2. What is center of mass? And derive the expression for finding its coordinates.

Solution: Center of mass is the point on an object, where the weight of the body acts.

Consider a body of total mass m and having center of mass as Cm.

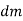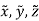A body is composed of an infinite number of particles of differential size. Consider one particle of mass , weight and location () as shown in figure

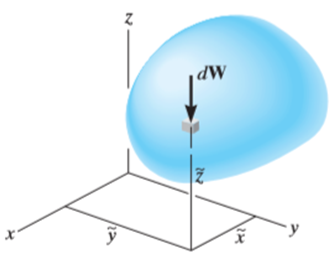
Weights of each particle will form an approximately parallel force system, and the resultant of this system is the total weight of the body W, which passes through a single point called the center of gravity G.

i.e. the weight of the body is the sum of the weights of all of its particles

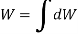
Also, mass of body is the sum of the mass of each particle of the body

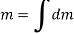
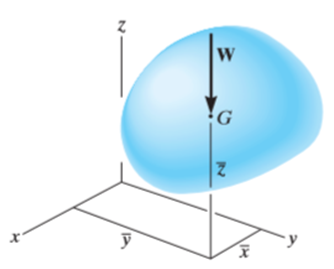
Now, the moment of W about x-axis is equal to the sum of moment of weights of each particles about same axis.

We get,

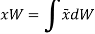
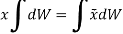
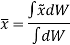
Now, as 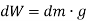and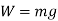

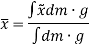
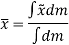
Similarly, if moments are summed about the y axis,

We get,

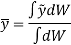
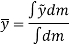
Now, consider that the body is fixed within the coordinate system and this system is rotated about the y axis as shown in fig

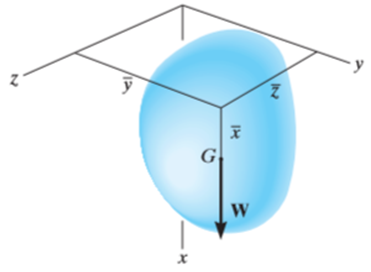
In similar manner, if moments are summed about the z axis, we get,

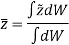
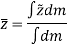
Hence, the location of center of mass with respect to x, y, z axes is

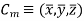
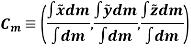
Q3. Explain mass moment of Inertia and radius of gyration.

Solution: The mass moment of inertia of a body is a measure of the body’s resistance to angular acceleration.

Consider a rigid body, rotating about z-axis, as shown in figure.

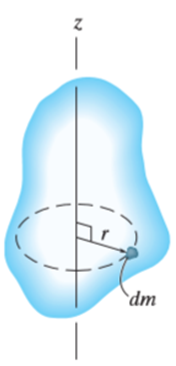
Mass moment of inertia is defined by,

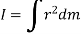
Where, r is the perpendicular distance from the axis of rotation to the arbitrary differential element of the body of mass dm.

The moment of inertia is also written as

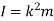
Where, m is the total mass of the body

And k is referred as radius of gyration

Radius of gyration for a body rotating about an axis is defined as the radial distance to a point which would have a same moment of inertia as the body’s actual distribution of mass, if the total mass of the plate were concentrated.

In simple words, radius of gyration is the perpendicular distance of the axis of rotation to the point where the entire mass of the body is supposed to be concentrated for dynamic analysis.

It is given by,

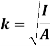
Q4. State and explain Theorem of parallel and perpendicular axes.

Solution: Theorem of parallel axes

Theorem of parallel axes states that, “the moment of inertia of the rotating body about an axis is equal to the summation of the moment of inertia of the body about an axis passing through the center of mass and the product of total mass of the body and the square of perpendicular distance between the two axes.”

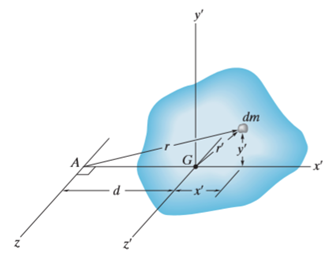
Mathematically,

Where,

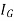= Moment of inertia about z’ axis passing through the center of mass G

m = total mass of body

d = perpendicular distance between the parallel axes

Theorem of perpendicular axes

It states that, “for the planar element, the moment of inertia about an axis is equal to the summation of moment of inertias about two mutually perpendicular axes.”

Mathematically,

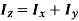
Q5. Explain General Plane motion.

Solution: General plane motion of a rigid body refers to a combination of translation and rotation motion.

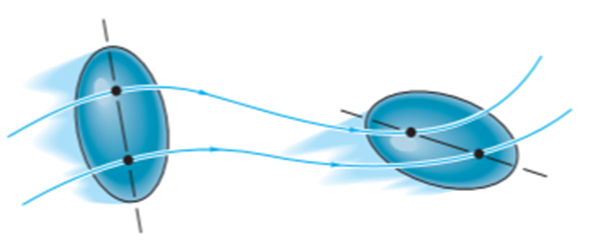
General planar motion refers to the simultaneous rotational and translational motion of a planar body in a 2-D plane.

General planar motion can be fully specified by knowing both the angular rotation of a line fixed in the body and the motion of a point on the body.

These motions can be related by using a rectilinear position coordinate s to locate the point along its path and an angular position coordinate 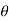to specify the orientation of the line. Then these two coordinates are related using the geometry of the problem. The following relation is found.

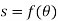
Differentiating the above equation, gives the relation between velocity 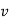and angular velocity .

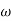Where,

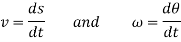
Then again differentiating, it yields to the relation between acceleration and angular acceleration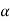

Where,

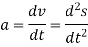
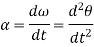
Q6. State and explain Chasle’s Theorem

Solution: Chasle’s Theorem states that, “Every spatial displacement can be referred as the composition of a rotation about some axis, and a translation along the same axis.”

Chasle's theorem applies only to rigid body displacements. It says that for rigid bodies, any given displacement can be treated as equivalent to a translation (T) along an axis and a rotation (R) about the same axis.

The axis that is mentioned above (usually refers to as the “Screw Axis”) need not necessarily passes through the body.

The translation and rotation order can be either translation followed by rotation or vice versa.

The word used above is “Displacement” which means that as per this theorem, the T+R combination (or the R + T combination) applied to the start point may result in the end point, but may not necessarily think of the difference between distance travelled and the corresponding displacement vector to visualize this better.

Mathematically,

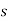is the resultant displacement

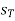is translational displacement

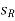is the rotational displacement

It used to find the displacement equation of a rigid body in general plane motion.

Q7. A cord is wrapped around a wheel which is initially at rest when 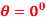. If a force is applied to the cord and gives it an acceleration 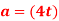m/s2 where t is in seconds, determine, as a function of time, (a) the angular velocity of the wheel, and (b) the angular position of line OP in radians.

Solution:

Q8. The motor shown in the photo is used to turn a wheel and attached blower contained within the housing. The details of the design are shown in Figure. If the pulley A connected to the motor begins to rotate from rest with a constant angular acceleration of , determine the magnitudes of the velocity and acceleration of point P on the wheel, after the pulley has turned two revolutions. Assume the transmission belt does not slip on the pulley and wheel.

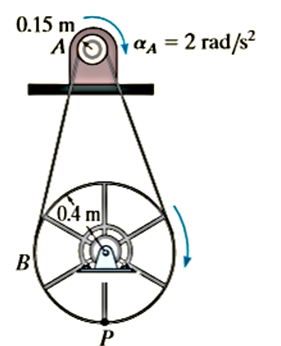
Solution:

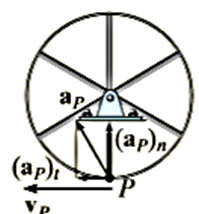
Q9. The end of rod R shown in Figure maintains contact with the cam by means of a spring. If the cam rotates about an axis passing through point O with an angular acceleration and angular velocity , determine the velocity and acceleration of the rod when the cam is in the arbitrary position .

Solution:

Q10. The large window in Figure is opened using a hydraulic cylinder AB. If the cylinder extends at a constant rate of 0.5 m/s, determine the angular velocity and angular acceleration of the window at the instant

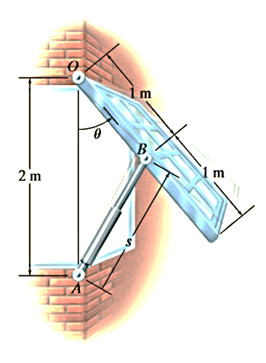
Solution:

Sign Up