Unit 6

Work and Energy

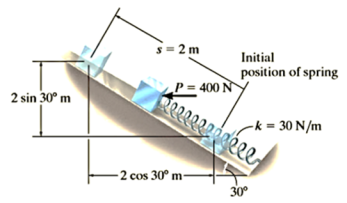
Q1) The 10-kg block shown in Fig. Rests on the smooth incline. If the spring is originally stretched 0.5 m, determine the total work done by all the forces acting on the block when a horizontal force pushes the block up the plane .

A1)

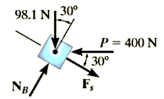
First the free-body diagram of the block is drawn in order to account for all the forces that act on the block

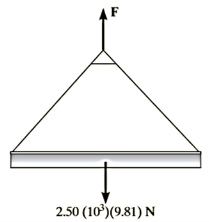
Q2) For a short time the crane lifts the 2.50-Mg beam with a force of Determine the speed of the beam when it has risen Also, how much time does it take to attain this height starting from rest?

A2)

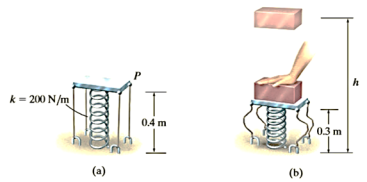
Q3) The platform P, shown in Figure a, has negligible mass and is tied down so that the 0.4-m-long cords keep a 1-m-long spring compressed 0.6 m when nothing is on the platform. If a 2-kg block is placed on the platform and released from rest after the platform is pushed down 0.1 m, Figure b, determine the maximum height h the block rises in the air, measured from the ground.

A3)

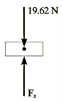
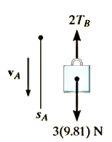
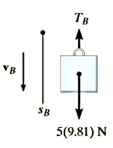
Q4) Blocks A and B shown in Figure below have a mass of 3 kg and 5 kg, respectively. If the system is released from rest, determine the velocity of block B in 6 s. Neglect the mass of the pulleys and cord.

A4)

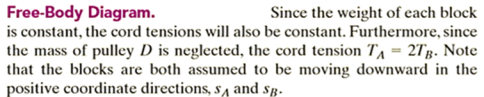
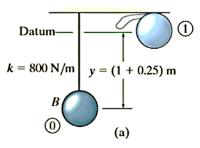
Q5) Ball B shown in Figure has a mass of 1.5 kg and is suspended from the ceiling by a 1-m-long elastic cord. If the cord is stretched downward 0.25 m and the ball is released from rest, determine how far the cord stretches after the ball rebounds from the ceiling. The stiffness of the cord is and the coefficient of restitution between the ball and ceiling is 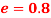. The ball makes a central impact with the ceiling.

A5)

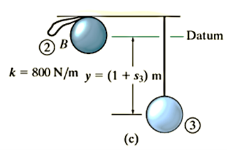
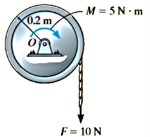
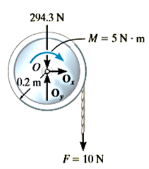
Q6) The 30–kg disk, shown in Figure, is pin supported at its center. Determine the number of revolutions it must make to attain an angular velocity of starting from rest. It is acted upon by a constant force which is applied to a cord wrapped around its periphery, and a constant couple moment . Neglect the mass of the cord in the calculation.

A6)

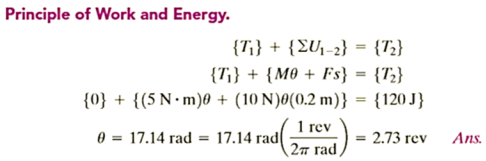
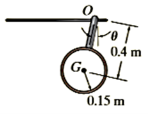
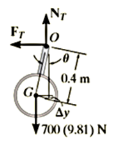
Q7) The 700-kg pipe is equally suspended from the two tines of the fork lift shown in the photo. It is undergoing a swinging motion such that when 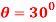it is momentarily at rest. Determine the normal and frictional forces acting on each tine which are needed to support the pipe at the instant 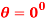. Measurements of the pipe and the suspender are shown in Fig. Neglect the mass of the suspender and the thickness of the pipe.

A7)

Q8) The 100-kg spool shown in Figure has a radius of gyration of 0.35 m. A cable is wrapped around the central hub of the spool, and a horizontal force having a variable magnitude of is applied, where t is in seconds. If the spool is initially at rest, determine its angular velocity in 5 s. Assume that the spool rolls without slipping at A.

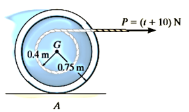
A8)

Q9) The Charpy impact test is used in materials testing to determine the energy absorption characteristics of a material during impact. The test is performed using the pendulum shown in Figure, which has a mass m, mass center at G, and a radius of gyration about G. Determine the distance from the pin at A to the point P where the impact with the specimen S should occur so that the horizontal force at the pin A is essentially zero during the impact. For the calculation, assume the specimen absorbs all the pendulum’s kinetic energy gained during the time it falls and thereby stops the pendulum from swinging when .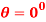

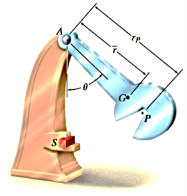
A9)

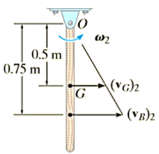
Q10) The 5-kg slender rod shown in Fig. 19–10a is pinned at O and is initially at rest. If a 4-g bullet is fired into the rod with a velocity of 400 m/s, as shown in the Figure, determine the angular velocity of the rod just after the bullet becomes embedded in it.

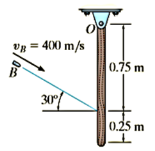
A10)