Unit - 2
Kinematics of Fluid Flow
Q1) Derive the Continuity Equation.
A1) The product of cross-sectional area of the pipe and the fluid speed at any point along the pipe is constant.
This product is equal to the volume flow per second or simply flows rate.
Mathematically it is represented as Av = Constant
Consider a fluid flowing through a pipe of non-uniform size. The particles in the fluid move along the same lines in a steady flow.
If we consider the flow for a short interval of time Δt, the fluid at the lower end of the pipe covers a distance Δx1 with a velocity v1, then: Distance covered by the fluid = Δx1 = v1Δt Let A1 be the area of cross section of the lower end then volume of the fluid that flows into the pipe at the lower end =V= A1 Δx1 = A1 v1 Δt
If ρ is the density of the fluid, then the mass of the fluid contained in the shaded region of lower end of the pipe is:
Δm1=Density × volume Δm1 = ρ1A1v1Δt ——– (1)
Now the mass flux defined as the mass of the fluid per unit time passing through any cross section at lower end is:
Δm1/Δt =ρ1A1v1 Mass flux at lower end = ρ1A1v1 ——————— (2)
If the fluid moves with velocity v2 through the upper end of pipe having cross sectional area A2 in time Δt, then the mass flux at the upper end is given by:
Δm2/Δt = ρ2A2v2 Mass flux at upper end =ρ2A2v2 ———————–(3)
Since the flow is steady, so the density of the fluid between the lower and upper end of the pipe does not change with time. Thus, the mass flux at the lower end must be equal to the mass flux at the upper end so:
ρ1A1v1 = ρ2A2v2 ———————-(4)
In more general form we can write: ρ A v =constant This relation describes the law of conservation of mass in fluid dynamics. If the fluid is in compressible, then density is constant for steady flow of in compressible fluid so ρ1 =ρ2
Now equation (4) can be written as: A1 v1 = A2 v2
In general: A v = constant
Q2) Calculate the velocity if 10 m3/h of water flows through a 100 mm inside diameter pipe. If the pipe is reduced to 80 mm inside diameter.
A2) Velocity of 100 mm pipe
Using the equation (2), to calculate the velocity of 100 mm pipe
(10 m3/h) (1/3600 h/s) =v100(3.14(0.1 m)2/4)
Or
v100= (10 m3/h) (1/3600 h/s) (3.14(0.1)2/4)
=0.35 m/s
Velocity of 80 mm pipe
Using the equation (2), to calculate the velocity of 80 mm pipe
(10 m3/h) (1/3600 h/s) =v80(3.14(0.08 m)2/4)
Or
v80= (10 m3/h) (1/3600 h/s) (3.14(0.08 m)2/4)
=0.55 m/s
Q3) Water is moving with a speed of 5.3 m/s through a pipe with a cross-sectional area of 4.8 cm24.8 cm2. The water gradually descends 11 m as the pipe increases to 8.3 cm28.3 cm2.
(a) What is the speed at the lower level?
(b) If the pressure at the upper level is 1.8×105 Pa1.8×105 Pa, what is the pressure at the lower level?
A3) Given Data:
- Initial velocity, v1=5.3m/sv1=5.3m/s.
- Initial area, A1=4.8cm2A1=4.8cm2.
- Final area, A2=8.3cm2A2=8.3cm2.
- Initial height, z1=11m, z1=11m.
- Final height, z2=0z2=0.
- Initial pressure, P1=1.8×
 Pa
Pa
P1=1.8×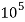 Pa.
Pa.
Specific weight of water, γ=9810N/m3=9810Pa/mγ=9810N/m3=9810Pa/m.
Part (a):
From the continuity equation, the final velocity is computed as follows:
Q2=Q1A2v2=A1v1v2=A1A2v1=
4.8cm2/8.3cm2*(5.3m/s)
≈3.1 m/s
Part (b)
By applying the Bernoulli's equation, the final pressure is determined as follows:
P2=P1+γ[v21−v222g+z1−z2]
= 1.8×105Pa+9810Pa/m [(5.32−3.0652) m2/s2/2(9.81m/s2) +11m−0]
≈3.0×105Pa
Q4) Define the term:
Stream line
Path line
Streak line
A4) Stream line:
A stream line is a continuous line in a fluid which shows the direction of the velocity of the fluid at each point along the line. The tangent to the stream line at any point on it is in the direction of the velocity at that point. Fluid particles lying on a stream line at an instant move along the stream line.
Path line:
A path line means the path or a line actually described by a single fluid particle as it moves during a period of time. The path line indicates the direction of the velocity of the same fluid particle at successive instants of time.
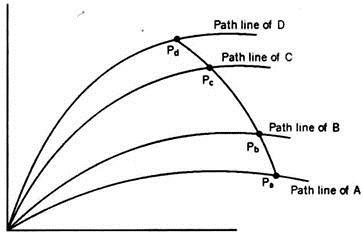
Streak line:
The streak line is the locus of the positions of fluid particles which have passed through a given point in succession. Suppose A, B, C, D… are fluid particles which passed through a reference point say the origin one after the other in succession. These particles have described their own path lines. Suppose at a time t, these particles A, B, C, D… are at Pa, Pb, Pc, Pd …. The line Pa, Pb, Pc, Pd …. Is the streak line, at time t.
Q5) Define and Derive equipotential line.
A5) A line, in which all line in which all points are at same voltage, is called equipotential line.
Equipotential lines are perpendicular to electric field.
Derivation:
This is a line along which the velocity potential ϕ is constant i.e., along this line dϕ=0.
But 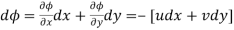
∴ For the equipotential line,
∴ 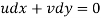
∴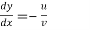 [Slope of equipotential line]
[Slope of equipotential line]
Q6) Derive Stream line equation.
A6) Stream line equation:
Consider a line of constant stream function, i.e., along this line
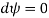
But
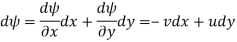
Therefore, for a line of constant stream function
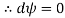
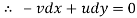
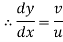
But we know v/u is the slope of the stream line.
∴ A line of constant stream function is a stream line.
Since the slope of the equipotential lies is 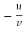 and the slope of the stream line is
and the slope of the stream line is  , it follows that at any point the equipotential line is orthogonal to the stream line.
, it follows that at any point the equipotential line is orthogonal to the stream line.
Condition for irrotational flow, we know for the condition of irrotational flow
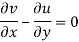
But we know 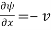
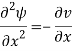
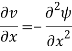
And 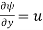

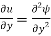
Then the condition 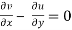 reduces to
reduces to
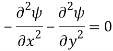
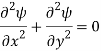
Q7) Describe Flow Net.
A7)
A grid obtained by drawing a series of stream lines and equipotential lines is known as a flow net.
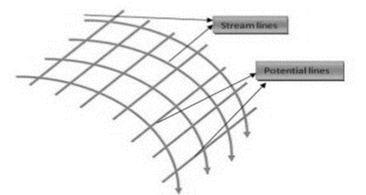
The stream lines and equipotential lines are mutually perpendicular to each other.
A flow net analysis assists in the design of an efficient boundary shapes.
It is also used to calculate the flow at ground level.
Flow nets provides information regarding two dimensional irrotational flow where it is difficult to go by mathematical solution.
Methods of drawing Flow nets
- Analytical Method
- Graphical method
- Hydraulic Models
- Electrical Analogy
Q8) Describe Irrotational Flow.
A8) Irrotational Flow:
Fluid elements moving in the flow field do not undergo any rotation,
ω = 0, ∇×V=0
The flow is irrotational if ω = 0 for every point.
The irrotational flow is always inviscid; i.e., Re>>1, but not turbulent and far from the boundaries where the viscous laminar layers are formed.
Subject to boundary conditions (usually no flow through a solid boundary) obtained when a body (e.g., an aerofoil) is placed in a flow which is uniform infinitely far upstream.
To satisfy boundary conditions one often constructs a composite solution. Note that if  and
and  are solutions to Eq. (1) then function
are solutions to Eq. (1) then function  is also a solution since:
is also a solution since:
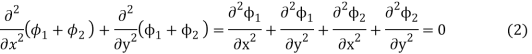
In general, then, if 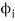 where
where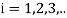 are each solution to laplace equation so must be
are each solution to laplace equation so must be
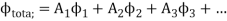
Where 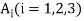 are constants.
are constants.
Q9) A liquid flows through a pipe with a diameter of 10cm at a velocity of 9cm/s. If the diameter of the pipe, then decreases to 6cm, what is the new velocity of the liquid?
A9) Rate of flow, A * v, must remain constant. Use the continuity equation, A1v1=A2v2.
Solving the initial cross-sectional area yields: A1=πr2=25πcm2. The initial radius is 5cm.
Then find the final area of the pipe: A2=πr2=9πcm2. The final radius is 3cm.
Using these values in the continuity equation allows us to solve the final velocity.
(25πcm2) (9cm/s) =(9πcm2) v2
v2=25cm/s
Q10) If blood flows through the aorta with velocity, va, with what velocity would blood flow through the capillaries in the body?
A10) Just like the volume flow rate equation for fluids, the flow rate of blood through the body is equal to area time velocity.
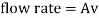
The flow rate is a constant, so depending on the area that the blood is travelling through, the velocity is constantly changing; therefore, the volume rate flow through the aorta is equal to the volume flow rate in capillaries.
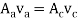
Because we can determine the area of the aorta and area of the capillaries, knowing the velocity through the aorta can give the velocity through the capillaries.
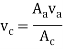
Q11) The velocity component is given by u=4y and v=-4x. Check whether the stream function is exists? If so, determine stream function
A11) Continuity Equation
Du/dx +dv/dy =0
d/dx(4y) +d/dy(-4x) =0
Hence the flow is possible the stream function is existing
By definition
v =d /dx = -4x
/dx = -4x
u = - d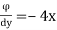
d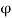 /dx =4x
/dx =4x
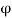 =x2 +y2
=x2 +y2
Integrating w.r.t x
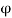 = 2x2 +f(y) ………………..(1)
= 2x2 +f(y) ………………..(1)
Differentiate w.r.t. y
-4y = f’(y)
Integrating w.r.t.y
 y2 =f(y)
y2 =f(y)
Put in equation (1)
 = 2 (x2 +y2 )
= 2 (x2 +y2 )
The stream line is a line at which the stream function is constant, therefore the equation of stream line is given by,
x2 +y2 =constant
Q12) Calculate the velocity at the point (3,3) for the following stream function;
 = ½ (y2- x2) +xy – 6
= ½ (y2- x2) +xy – 6
A12) Given: x=3, y=3
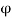 = ½ (y2- x2) +xy – 6
= ½ (y2- x2) +xy – 6
Velocity component
u = - d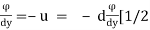 (y2- x2) +xy – 6]
(y2- x2) +xy – 6]
u=-[1/2(2y)+x]
=-(y+x)
=-(3+3)
=-6 m/sec
v =d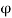 /dx
/dx
= d/dx[ 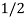 (y2- x2) +xy – 6]
(y2- x2) +xy – 6]
= -x+y =-3+3=0
Hence the velocity at point (3,3)
V =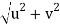
V = 6m /sec
Q13) Air flows into a jet engine at 5 kg/sec while fuel flow into the jet is at 0.1 kg/sec. The burned gases leave at the exhaust which has cross area 0.1m2 with velocity of 500 m/sec. What is the density of the gases at the exhaust?
A13) The mass conservation equation is used. Thus, the flow out is (5 + 0.1 )5.1 kg/sec
The density is
ƍ = m˙/AU
= 5.1 kg/sec/0.01m2 X500 m/sec
ƍ = 1.02kg/m3
Q14) The continuity and momentum equations for 2-D flow for a cylindrical coordinate system are: ∂u/∂x + 1/r. ∂ (rv) /r =0
A14)
u ∂u/ ∂x +v/r. ∂(ur)/ ∂r = 1/ ρ. ∂p/∂x + v[∂2u/ ∂x2 +1/r (∂/∂r) (r∂u/∂r)]
u ∂v/ ∂x +v/r. ∂(vr)/ ∂r = -(1/ ρ). ∂p/∂r + v[∂2v/ ∂x2 +1/r (∂/∂r) (r∂v/∂r)]
Where u and v are velocity components in x and r direction respectively. Simplify the above equations to obtain the momentum equation for hydro dynamically fully developed flow in a circular tube. Use the resulting equation and appropriate boundary condition to obtain velocity distribution for hydro dynamically fully developed flow in a circular tube. Find mean velocity um and express the velocity distribution in form of u/um = f(r).
Q15) The velocity potential function is given by an expression
ɸ =-xy3 /3 –x3 +x3y/3 +y2
Find the velocity components in x and y directions
A15) The velocity potential function is given by
ɸ =-xy3 /3 –x3 +x3y/3 +y2
By definition
u = - 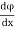 and v =d
and v =d /dy
/dy
Velocity component is given by
V = d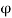 /dy
/dy
= x y 2 –x 3/3 -2y
u = - d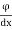
= y3 /3 +2x –x2 y
Q16) Stream function is given by the expression  = 2x2- y3) ,find component of velocity as well as the resultant velocity at point (3,3)
= 2x2- y3) ,find component of velocity as well as the resultant velocity at point (3,3)
A16) Stream function 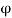 = 2x2- y3
= 2x2- y3
Velocity at point P , x =3, y=3)
By definition
u = - 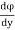
= - 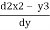
= -(-3y2)
u =27 units
v =d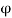 /dx
/dx
= d/dx(2x2- y3)
=4x
v =12 units
Resultant velocity
V =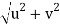
V = 29.546 unit
Direction of velocity
Θ = tan-(v/u)
Θ =23.96 0