Unit - 4

Fluid Dynamics

Q1) Explain Boundary layer with diagram.

A1) Boundary layer is the thickness of that layer next to a surface in which the velocity grows from zero to a maximum value (or so close to a maximum as to be of no practical difference). This thickness is usually given the symbol δ (small delta).

The boundary layer, once established may have a constant thickness but, for example, when a flow meets the leading edge of a surface, the boundary layer will grow as shown in figure below.

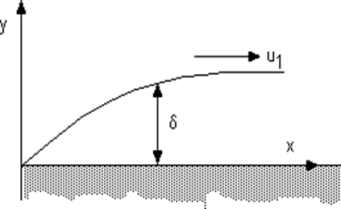
• Boundary layer is defined as:
• The boundary layer of a flowing fluid is the thin layer close to the wall.
• In a flow field, viscous stresses are very prominent within this layer.
• Although the layer is thin, it is very important to know the details of flow within it.
• The main-flow velocity within this layer tends to zero while approaching the wall (no-slip condition).
• Also, the gradient of this velocity component in a direction normal to the surface is large as compared to the gradient in the stream wise direction.

Q2) What is fluid dynamics? list the various forces acting on fluid mass. Explain the significance of each.

A2) The study of force which produced motion in a fluid is called as fluid dynamics

Newton’s second law of motion is the fundamental principle on which fluid dynamics are based. It states that, the resultant force on the fluid element is directly proportional to the rate of change of momentum and take place in the direction of force.

Net force = mass X acceleration

ƩF      =m. a

Forces acting on fluid -

Gravity force (Fg)

Pressure force (Fp)

Viscous force (Fv)

Turbulent force (Ft)

Compressibility force (Fc)

1.gravity force (Fg) –it is due to weight of the fluid

2. Pressure force (Fp) –It is due to pressure gradient between two points in the direction of flow

3.Viscous force (Fv) –It is due to viscous property of the flowing fluid

4. Turbulent force (Ft)- It is due to turbulence of the flow.

5. Compressibility force (Fc)-It is due to elastic property of fluid.

Net force = Fg +Fp +Fv +Ft

This equation is called as Reynold’s equation of motion.it is useful in the study of turbulent flows. If compressibility and turbulence effects on the fluid is neglected then,

Net force = Fg +Fp +Fv

This equation is called as Navier –Stokes’s equation of motion. If fluid flow is considered as an ideal flow, then

Net force = Fg +Fp

This equation is called as Euler’s E\equation of motion.

Q3) Elaborate displacement thickness briefly.

A3) Displacement Thickness:

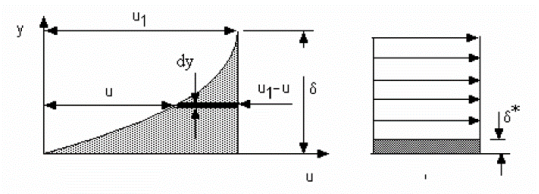
The flow rate within a boundary layer is less than that for a uniform flow of velocity u1. The reduction in flow is equal to the area under the curve in fig. If we had a uniform flow equal to that in the boundary layer, the surface would have to be displaced a distance 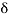* inorder to produce the reduction. This distance is called the displacement thickness and it isgiven by:

Another interpretation of the displacement thickness is that because the volumetric flow in the boundary layer is actually 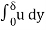the same flow would be achieved if the wall was displaced upward into the flow in an amount 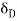since the definition can be written in the form

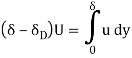
Q4) Describe Momentum thickness.

A4) Momentum Thickness

Momentum Thickness, θ Momentum thickness is the distance that, when multiplied by the square of the free stream velocity, equals the integral of the momentum defect. Alternatively, the total loss of momentum flux is equivalent to the removal of momentum through a distance θ. It is a theoretical length scale to quantify the effects of fluid viscosity near a physical boundary.

Momentum thickness is given by:

The momentum in a flow with a boundary layer present is less than that in a uniform flow of the same thickness. The momentum in a uniform layer at velocity 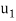and height h is h. When a boundary layer exists, this is reduced by 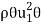.   Where, 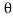is the thickness of the uniform layer that contains the equivalent to the reduction.

If density is constant, this simplifies to

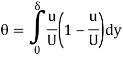
Q5) Explain Energy thickness in fluid mechanics.

A5) Energy thickness (δe):

Energy thickness (δe) is defined as the thickness of an imaginary layer in free stream flow which has energy equal to the deficiency of energy caused to actual mass flowing inside the boundary layer.

By equating the energy transport rate for velocity defect to that for ideal fluid

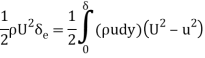
If density is constant, this simplifies to

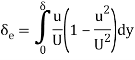
Q6) Derive the expression for displacement thickness.

A6) Consider a fluid moving with a velocity U approaching a flat plate at rest as shown in Figure mentioned below:

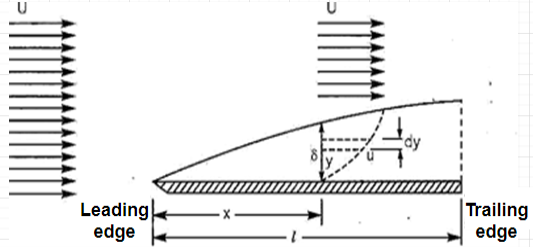
At a section distance x from the leading edge, let δ be the thickness of the boundary layer. At this section the velocity varies from zero at the plate to U at a distance δ from the plate.

Consider unit width of the plate. Consider an elemental strip (1 x dy) distance y from the plate. Let u be the velocity at this level.

Mass flowing per second through the elemental strip = ρudy

If the plate had not been present the mass flowing per second through the above elemental strip would have been ρUdy.

∴ Reduction in mass flowing per second through the elemental strip

= ρ (U – u) dy

∴ Total reduction in mass flowing per second due to the plate –

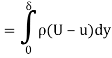
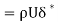
Let the above quality be

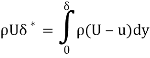
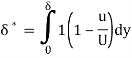
Suppose the plate is displaced normal to itself by δ* and the velocity is uniform at the value U, then the mass of fluid passing through the strip of thickness δ* will be ρUδ *. The depth δ* is called displacement thickness.

Q7) Derive the expression for momentum thickness. Explain it.

A7) Consider the flow through an elemental strip of area (1. Dy) distance y from the boundary.

Mass flowing per second through the elemental strip = ρudy

Let us consider the above quantity of the fluid.

Momentum of this quantity = (ρudy) u = ρu2dy

Momentum of this quantity in the absence of the boundary layer = (ρudy) U

Loss of momentum per second-

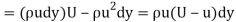
Total loss of momentum per second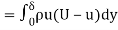

Let the above quantity be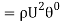

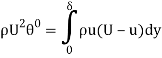
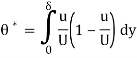
The momentum thickness θ* may be visualized as the depth of flow with uniform velocity U, so as to have a momentum per second equal to the loss of momentum per second due to boundary layer. For a depth of flow θ* with a velocity V momentum per second per unit width

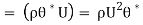
The depth θ* is called momentum thickness.

Q8) Derive the expression for the energy thickness.

A8) Consider the flow through an elemental strip (1. Dy) distant y from the boundary. Mass flowing per second through the elemental strip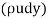

Kinetic Energy of this quantity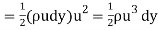

Kinetic energy of this quantity in the absence of the boundary layer

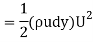
∴ Loss of kinetic energy

∴ Total Loss of kinetic energy

Suppose δ** is the depth of flow with uniform velocity U so as to have a kinetic energy equal to the loss of kinetic energy due to the boundary layer.

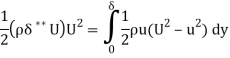
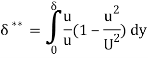
The depth δ** is called energy thickness.

Q9) Find the displacement thickness 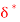for a laminar BL modelled by the equation

A9)

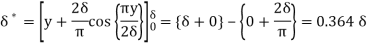
Q10) The velocity distribution inside a laminar BL over a flat plate is described by the cubic law 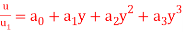. Show that the momentum thickness is 39δ/280.

A10) At 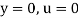so it follows that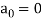

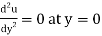so as 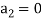. Show for yourself that this is so.

The law is reduced to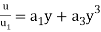

At y=δ, 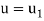so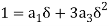

Hence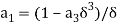

Now differentiate and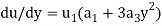

At 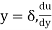is zero 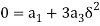so so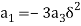

Hence by equating 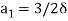and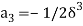

Now we can write the velocity distribution as

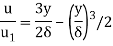
If we give term the symbol we η may be rewrite the equation as

The momentum thickness θ is given by

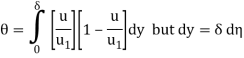
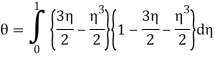
Integrating gives

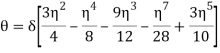
Between the limits 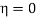and 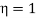this evaluates ot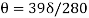

Q11) Show that the mean velocity in a pipe with fully developed turbulent flow is 49/60 of the maximum velocity. Assume the 1/7th law.

A11) For a pipe, the B.L. Extends to the centre so δ=radius=R. Consider an elementary ring of flow.

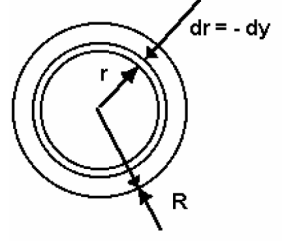
The velocity through the ring is u.

The volume flow rate through the ring is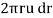

The volume flow rate in the pipe is

Since 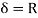then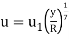

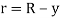
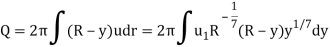
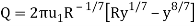
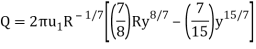
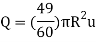
The mean velocity is defined by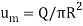

Hence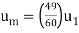 

Q12) Consider the two-dimensional, incompressible, steady flow of a fluid of constant viscosity in the entrance region of a slit of width 2h. The flow enters the tube (x = 0) with the uniform velocity V. At distance x from the entrance, the boundary layer thickness is δ, and the core flow has the speed U. The boundary layer is laminar.

µ/ U = 2(y/δ) – (y/δ )2

A12) Velocity profile in boundary layer assumed parabolic and it is gives

µ/ U = 2( y/δ) – (y/δ )2                         in 0 ≤ y ≤ δ

In δ ≤ y ≤ h

Let’s apply mass conservation to determine U = U(x). At region (1) and (2), the volume flow rates are    respectively

∫h 0 V dy = V h

∫h 0   u dy = ∫h 0 2U y/ δ − U (y /δ)2 dy + ∫h 0   U dy

= U/ δ y2 – (U /3 δ) y3+ U(h – δ)

=U(h-1/3 δ

V      =  U(1-1/3h δ)

Now let’s consider Karman momentum integral equation

d/dx (U 2 θ + δ∗U(du/dx)  =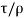

Where the displacement thickness δ∗ and momentum thickness θ are defined as

δ∗    = ∫ (1-u/U dy), θ =u/U= ∫ (1-u/U dy)

The differential equation can be simplified as

Vh     = 2 + 7/3δ / (1-3 δ)2 dδ = 30ν

Q13) If the velocity distribution in laminar boundary layer over a flat plate is assumed to be given by second order polynomial u=a+by+cy2, determine its form using necessary boundary condition

A13) Velocity distribution: u=a+by+cy2

Following boundary condition must be satisfied

(i)                At y =0, u =0

0=a+0+0

a =0

(ii)              At y =δ, u =U

U =0 +b δ +c δ2 

U   = b δ +c δ2  )    ……………………..(1

(iii)           At    y = δ, du/dy =0

(du/dy) y= δ      =d/dy(a+by+cy2)

0=b+2cy

Put y = δ

b =-2c δ ………………………….(2)

Put the value of b in 1st eqn

U= -c δ2

C =-U/ δ2 ………………………(3)

Put these value in eqn 2 & 3

  b =-2(-U/ δ2 ) δ

b =2U/ δ

Put value of a, b, and c in velocity distribution eqn

u =0+(2U/ δ) y +(-U/ δ2) y2

u =2U (y/ δ) –U (y/ δ)2

Q14) Velocity distribution in a boundary layer is given below find whether flow is attached or detached 

u/U =3/2(y/ δ)-1/2(y/δ)3

A14)

u/U =3/2(y/ δ)-1/2(y/δ)3

u    = (3/2) u (y/ δ)-U/2(y/δ)3

Diff. w.r.t. y

Du/dy =3/2 (U/ δ) –U/2(3y2/ δ3)

At y =0

(du/dy) =3U/2 δ - U/2 X 0

=  3/2( U/ δ)

As the value (du/dy) at y= 0 is positive, hence flow is attached

Q15) Velocity distribution in a boundary layer is given below check whether flow is attached or detached or on the verge of separation

u/U =2(y/ δ)2 + (y/δ)3 -2 (y/δ)4

A15) u/U =2(y/ δ)2 + (y/δ)3 -2 (y/δ)4

u = 2 U (y/ δ)2 +U (y/δ)3 -2U (y/δ)4

Diff w.r.t y

Du/dy =4Uy/ δ +3Uy2/ δ3 -8Uy3/ δ4

Du/dy =4Uy/ δ +3U/ δ (y/ δ)2 -8U/ δ (y/ δ)3

At y =0

Du/dy    =4U/ δ (0) +3 U/ δ (0/ δ)2 -8U/ δ (0/ δ)3

= 0

Hence flow is on the verge of separation