Unit - 5

Laminar Flow

Q1) Lubricating oil of specific gravity 0.84 and dynamic viscosity 0.137Ns/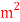 pumped at a rate of 0.024 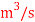through a 0.17m diameter 400m long horizontal pipe and the power required to maintain flow.

Given data:

Specific gravity of oil, S=0.84

Dynamic viscosity of oil, μ=0.137Ns/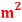

Rate of flow, Q =0.024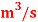

Diameter of pipe, D=0.17m

Length of pipe, L = 400m

A1) From Hagen-Poiseuille equation, Pressure drop, (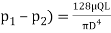

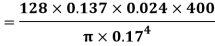
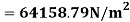
Shear stress at the pipe wall,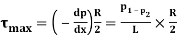

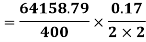
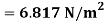
Q2) The Velocity distribution in laminar boundary layer is given by

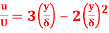. Where, 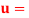Velocity at a distance y from the boundary

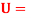Velocity at a distance δ, the thickness of the boundary layer.

Calculate:

(i) The ratio of displacement thickness to boundary layer thickness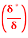

(ii) The ratio of momentum thickness to boundary layer thickness

A2) Velocity distribution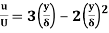

(i) Ratio of displacement thickness to boundary layer thickness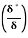

We know that,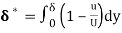

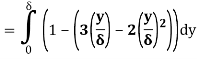
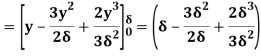
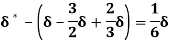
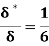
(ii) The ratio of momentum thickness to boundary layer thickness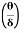

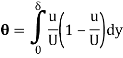
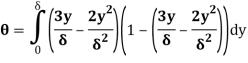
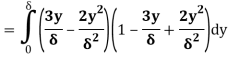
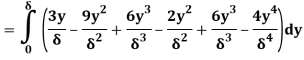
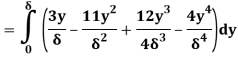
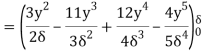
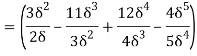
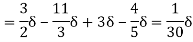
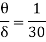
Q3) Explain turbulent through pipes.

A3) Eddy currents are present within the flow and the ratio of the internal roughness of the pipe to the internal diameter of the pipe needs to be considered to be able to determine the friction factor. In large diameter pipes the overall effect of the eddy currents is less significant. In small diameter pipes the internal roughness can have a major influence on the friction factor. The relative roughness of the pipe and the Reynolds number can be used to plot the friction factor on a friction factor chart. The friction factor can be used with the Darcy-Weisbach formula to calculate the frictional resistance in the pipe. Between the Laminar and Turbulent flow conditions (Re 2300 to Re 4000) the flow condition is known as critical. The flow is neither wholly laminar nor wholly turbulent. It may be considered as a combination of the two flow conditions. The friction factor for turbulent flow can be calculated from the Colebrook-White equation:

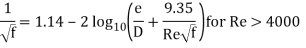
Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. The mixing action of the turbulent flow enhances the temperature averaging effect in addition to the transfer of energy from the hot water to the surrounding fluid. When a hot object is cooled, the mixing action of turbulent flows in the fluid surrounding the object plays an important role in cooling it.

Q4) Explain Darcy- Weibach equation.

A4) In the design of piping systems the choice falls between the selection of diameter and the pressure drop. The selection of a larger diameter leads to higher initial cost. But the pressure drop is lower in such a case which leads to lower operating cost. So, in the process of design of piping systems it becomes necessary to investigate the pressure drop for various diameters of pipe for a given flow rate. Another factor which affects the pressure drop is the pipe roughness. It is easily seen that the pressure drop will depend directly upon the length and inversely upon the diameter. The velocity will also be a factor and in this case the pressure drop will depend in the square of the velocity (refer Bernoulli equation).

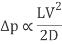
Hence, we can say that

The proportionality constant is found to depend on other factors. In the process of such determination Darcy defined or friction factor f as

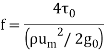
This quantity is dimensionless which may be checked. Extensive investigations have been made to determine the factors influencing the friction factor. It is established that in laminar flow f depends only on the Reynolds number and it is given by

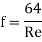
In the turbulent region the friction factor is found to depend on Reynolds number for smooth pipes and both on Reynolds number and roughness for rough pipes. Some empirical equations are given in section and also under discussions on turbulent flow. The value of friction factor with Reynolds number with roughness as parameter is available in Moody diagram. Using the definition of Darcy friction factor and conditions of equilibrium, expression for pressure drop in pipes is derived in this section. Consider an elemental length L in the pipe. The pressures at sections 1 and 2 are P1 and P2.

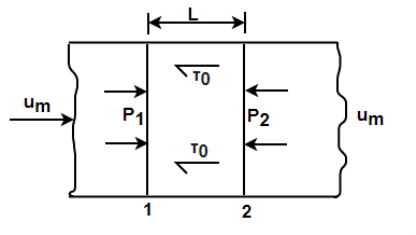
The other force involved on the element is the wall shear t0.

Net pressure force in the element is (P1 –P2)

Net shear force in the element is t0 PDL

Force balance for equilibrium yields

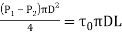
From the definition friction factor

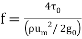
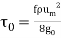
Substituting and letting (P1 –P2) to be ΔP.

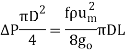
This reduces to

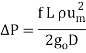
This equation known as Darcy-Weisbach equation and is generally applicable in most of the pipe flow problems. 

Q5) Water flows in a steel pipe (d = 40 mm, k = 0.045x10-3 m, µ = 0.001 k/ms) with a rate of 1 lit/s. Determine the friction coefficient and the head loss due to friction per meter length of the pipe using: 1- Moody chart? 2- Smooth pipe formula?

A5) v = Q / A = 0.001 / (π (0.04)2 /4) = 0.796 m/s 

Re = ρ v d / µ = (1000x0.796x0.04) / 0.001 = 31840 > 4000

 Turbulent flow.

1. Moody chart:

k/d = 0.045x10-3 / 0.04 = 0.0011 & Re = 31840 from the chart, f = 0.0065 hf = 4 f L v 2 = 4x0.0065x1x(0.796)2 = 0.0209 m / m of pipe 2 g d 2x9.81x0.04

2.     Smooth pipe (Blasius equation):

f = 0.079 / Re 0.25 = 0.079 / (31840) = 0.0059

Hf = 4 f L v 2 /2gd

= 4x0.0059x1x(0.796)2/2x9.81x0.04

= 0.02 m / m of pipe

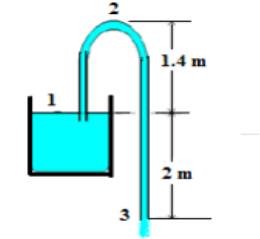
Q6) The pipe of a syphon has 75 mm diameter and discharges water to the atmosphere, as shown in figure. Neglect all possible losses. a. Determine the velocity of flow? b. Find the discharge? c. What is the absolute pressure at the point 2?

A6)

(a)   Applying Bernoulli’s equation between (1) and (3), 2 + 0 + 0 = 0 + 0 + (v 2 3/2g)

v3 = 6.26 m/s

(b) Q = v3 x A = 6.26 x (π (0.075)2 /4) = 0.028 m3 /s

(c) Applying Bernoulli’s equation between (1) and (2),

2 + 0 + 0 = 3.4 + P2/ρg + (6.262 /2g)

P2 = - 3.397 x (1000 x 9.81) = - 33327.8 N/m2 = - 33.33 kPa

P2abs = 64.77 kPa where, (Patm = 98.1 kN/m2)

Q7) A pipe, 40 m long, is connected to a water tank at one end and flows freely in atmosphere at the other end. The diameter of pipe is 15 cm for first 25 m from the tank, and then the diameter is suddenly enlarged to 30 cm. Height of water in the tank is 8 m above the centre of pipe. Darcy’s coefficient is 0.01. Determine the discharge neglecting minor losses?

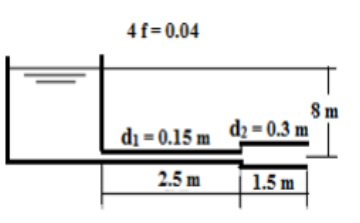
A7) Loss due to friction, hLf = hf1 + hf2

hf=32fLQ2/ 2 gd5

f = 0.01

Total losses, hT = Q2 ((32 f L1/ 2 gd15)+ (32 f L2 )/  2 gd2 5 ))

8 = Q2 ((32x0.01) x (25)/(π2g(0.15)5 +(32 x0.01 x15)/ (π2g(0.3)5

Q8) Two reservoirs have 6 m difference in water levels, and are connected by a pipe 60 cm diameter and 3000 m long. Then, the pipe branches into two pipes each 30 cm diameter and 1500 m long. The friction coefficient is 0.01. Neglecting minor losses, determine the flow rates in the pipe system?

A8) hf = hf1 + hf2

6 = hf1 + hf2

6 = k1 Q12 + k2 Q22

k1 = 32 f1 L1/2gd15= 32*0.01*3000/2×9.81×(0.65)5 = 127.64

k2 = 32 f2 L2/2gd25 = 32*0.01*1500//2×9.81×(0.3)5  = 4084.48

k2 = 32 k1

 6 = k1 Q1 2 + 32 k1 Q2 2

hf2 = hf3       &  k2 = k3        Q2 = Q3

Q1 = Q2 + Q3 = 2 Q2 

 6 = k1 Q12 + 8 k1 Q12 = 9 k1 Q1 2 = (9 * 127.64) Q12

= 1148.76 Q12 

  Q1 = 0.072 m3/s &

Q2 = 0.036 m3/s

Q9) Define friction factor for smooth and rough surface.

A9) The friction factor or Moody chart is the plot of the relative roughness (e/D) of a pipe against the Reynold's number. The blue lines plot the friction factor for flow in the wholly turbulent region of the chart, while the straight black line plots the friction factor for flow in the wholly laminar region of the chart.

Q10) Describe Moody’s Diagram.

A10) The Moody chart or Moody diagram is a graph in non-dimensional form that relates the Darcy-Weisbach friction factor, Reynolds number and relative roughness for fully developed flow in a circular pipe. It can be used for working out pressure drop or flow rate down such a pipe.

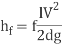
Pressure drop can then be evaluated as:

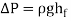or directly from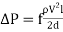

Where the density of the fluid is, is the average velocity in the pipe, is the friction factor from the Moody chart, is the length of the pipe and is the pipe diameter.

The Moody chart can be divided into two regimes of flow: laminar and turbulent. For the laminar flow regime, the Darcy–Weisbach friction factor was determined analytically by Poiseuille and   is used. In this regime roughness has no discernible effect. For the turbulent flow regime, the relationship between the friction factor and the Reynolds number is more complex and is governed by the Colebrook equation which is implicit in 

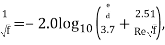turbulent flow.

In 1944, Lewis Ferry Moody plotted the Darcy–Weisbach friction factor into what is now known as the Moody chart.

Q11) On a circular conduit there are different diameters: diameter D1 = 2 m changes into D2 = 3 m. The velocity in the entrance profile was measured: v1 = 3 m/s. Calculate the discharge and mean velocity at the outlet profile (see fig. 1). Determine also type of flow in both conduit profiles (whether the flow is laminar or turbulent) – temperature of water T = 12° C. Discharge Q and consequently velocity v2 can be calculated from the continuity equation.

A11) Q= v1.s1   = v1 (  D1 2 )  /4 = 3 22 /4   =9425 m3/s

V2 = Q/s2 = 9425/(  D2 2) /4            = 1333 m/s

To determine type of flow in conduit,

The Reynolds number Re v.D /    will be used.

For laminar flow: Re2320

For turbulent flow Re2320

Kinematic viscosity of water of 12°C   124 X10-6  m2 / s for the conduit: 4838,1.10 2320 1

For the conduit:

Re1 =  v1 .D 1/   =3.2/124 X10-6  m2 / s

           =    4838,1X103                              2320  turbulent flow

Re2  =  v2 .D 2/  

         = 1333.3/124 X10-6  m2 / s

        =3225X103                                              2320 turbulent flow                  

Q12) Water flows in the pipeline (see fig). Calculate maximum velocity umax in the pipe axis and discharge Q. Determine whether the flow is laminar or turbulent (T = 12oC). The mercury differential manometer (Hg = 13600 kgm-3) shows the difference between levels in Pitot tube Hm = 0,02 m. Diameter of the pipe is D = 0,15 m. Velocity coefficient of Pitot tube is  = 1,0. Mean velocity is considered to be v = 0,84 u   

A12) The difference between velocity heads in profiles 1 and 2 (in profile 2 the velocity head is given by velocity u max, in profile 2 the velocity head is zero, because in manometer there is no velocity) will cause a difference between pressure heads. Consequently, it causes a change in mercury levels in manometer. To determine the point velocity, combination of equation of pressure balance (at convenient surface area in manometer) will be used in combination with Bernoulli equation for profiles 1 and 2.

Determination of pressure difference (balance of static pressures at surface area).

P1 +  hg g Hm   =P2 +  w g Hm

P1-P2 = Hm   X g (hg     -w   )

(P1  -   P2)/ w   .g  = Hm(hg     /w   -1)

Determination of point velocity (from Bernoulli equation for profiles 1 and 2, datum level at pipe

P1/  g  + α U2 /2g     =    P2/ g  +Z12

After equation arrangement, including introduction of a new coefficient  ,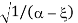

It comes to

Umax =  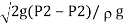

If loss is neglected ς = 0  φ = 1

Umax        =     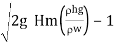

                 =   

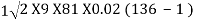
                 =      2224 m/s

Using the relation between point and mean velocity v = 0,84 umax, mean velocity will be determined and, consequently, continuity equation will be used to calculate discharge Q.

v = 0,84 umax   =1868 m/s

Q =v .s = Q(  D 2 )  /4          =0.033 m3/s

Flow regime will be determined using the Reynolds number:

Re       v D /

1868.015 /124 X10 -6    =225943

 The value of Reynolds number Re > 2320  flow in the pipeline is turbulent.

Q13) For turbulent flow through a pipe having wall shear stress 10 N/m 2, size of the surface imperfection is k=0.03 mm. Assuming the kinematic viscosity of water 1 X10 m 2/sec, find whether pipe behave as hydro dynamically rough, smooth or transitional

A13) Given: shear stress, =10 N/m2

Size of surface imperfection k    0.03 mm =0.03 X10-3 m

Kinematic viscosity  ν     =1X 10 m-4 m2/sec

Density water 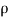   =1000 kg/m

Shea stress     µ   =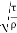

=

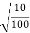
=0.1 m/s

Roughness Reynold’s number

Re =       µ k/ ν

=0.1 X0.03 X10-3 /1X 10-4

= 0.03 < 4

Re is less than 4, between 4 and 100, and hence pipe surface behaves as smooth.

Q14) A pipe line carrying oil s =0.8 has average height of irregularities projecting from the surface of the boundary of pipe as 0.3 mm. What type of boundary is it? the shear stress developed is 3 N/m2. Take kinematic viscosity ν=0.012 stoke

A14) Given:

Average height of irregularities K=0.3 mm =0.3 X10-3

Shea stress 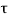   =3 n/mm2

Specific gravity of oil = s =0.8

Density                         = 800 kg3

Kinematic viscosity  = 0.012 stoke =0.012 X10-4   m2/s  

Shear stress,

µ   =     =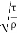      

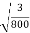
= 0.061 m/sec

Roughness of Reynolds’s Number

Re     =       µ k/ ν

=0.1 X0.3 X10--5/0.0121X 10-4

= 15.25 > 4 but<100

The surface boundary is transition

Q15) Water flows in a steel pipe (d = 40 mm, k = 0.045x10-3 m, µ = 0.001 k/ms) with a rate of 1 lit/s. Determine the friction coefficient and the head loss due to friction per meter length of the pipe using:  Moody chart

A15) Given      d=40 mm,   k =0.045x10-3 m

µ      = 0.001 k/ms

v = Q / A

= 0.001 / (π (0.04)2 /4)

= 0.796 m/s

Re = ρ v d / µ

= (1000x0.796x0.04) / 0.001

= 31840 > 4000

Turbulent flow.

By using Moody chart:

k/d = 0.045x10-3 / 0.04 = 0.0011   &             Re = 31840

from the chart, f = 0.0065

Hf = 4 f L v2 /2 g d

= 4x0.0065x1x(0.796)2 / 2x9.81x0.04

= 0.0209 m / m of pipe