Unit - 6

Dimensional Analysis and Hydraulic Similitude

Q1) Why it is necessary to have dimensional reason? Explain.

A1) We make use of dimensional analysis for three prominent reasons:

• To check the consistency of a dimensional equation.
• To derive the relation between physical quantities in physical phenomena.
• To change units from one system to another.

Understanding dimensions is of utmost importance as it helps us in studying the nature of physical quantities mathematically. The basic concept of dimensions is that we can add or subtract only those quantities which have same dimensions. Also, two physical quantities are equal if they have same dimensions.

Dimensional analysis is a mathematical technique used to predict physical parameters that influence the flow in fluid mechanics, heat transfer in thermodynamics, and so forth. The analysis involves the fundamental units of dimensions MLT: mass, length, and time.

A typical fluid mechanics problem typical fluid mechanics problem in which experimentation is required consider the experimentation is required consider the steady flow of a steady flow of an incompressible Newtonian fluid through a long, smooth incompressible Newtonian fluid through a long, smooth walled, horizontal, circular pipe.

The first step in the planning of an experiment to study this problem would be to decide the factors, or variables, that will have an effect on the pressure drop.

Pressure drops per unit length p  f (D,  ,  , V).

Q2) Explain the two different methods for dimensional analysis.

A2) It the number of variables involved in a physical phenomenon are known, then the relations among variables can be determined by the two methods, mentioned below:

1. Rayleigh’s Method
2. Buckingham’s Pi theorem

1. Rayleigh’s Method:

It is used for determining expression for variable (dependent) which depends on maximum three to four variables (independent) only.

2.     Buckingham’s Pi theorem:

Several methods can be used to form the dimensionless products, or pi term, that arises in a dimensional analysis.

Regardless of the method to be used to determine the dimensionless products, one begins by listing all (dimensional) variables that are known (or believed) to affect the given flow phenomenon.

Eight steps listed below outline a recommended procedure for determining the Π terms.

Steps 1: List all the variables.

List all the dimensional variables involved.

Keep the number of variables to a minimum, so that we can minimize the amount of laboratory work.

All variables must be independent. For example, if the cross -sectional area of a pipe is an important variable, either the area or the pipe diameter could be used, but not both not both, since they are obviously not independent.

Step 2: Express each of the variables in terms of in terms of basic dimensions and find the number of references the number of reference dimensions.

Step 3: Determine the required number of pi terms.

Let k be the number of variables in the problem.

Let r be the number of reference dimensions (primary dimensions) required to describe these variables.

The number of pi terms is k-r

Example: For pressure drop per unit length k=5, r = 3, the number of pi terms is k-r=5-3=2.

Step 4: Select number of repeating variables, where the number required is equal to the number of reference dimensions.

Step 5: Form a pi terms by multiplying one of the non-repeating variables by the product of the repeating variables, each raised to an exponent that will make the combination dimensionless.

Step 6: Repeat Step 5 for each of the remaining non-repeating variables.

Step 7: Check all the resulting pi terms to make sure they are dimensionless.

Step 8: Express the final form as a relationship among the pi terms, and think about what is means.

Q3) What is similitude and mention its type?

A3) Similitude is a concept used in testing of engineering models. Usually, it is impossible to obtain a pure theoretical solution of the hydraulic phenomenon.

Therefore, experimental investigations are often performed on small scale models, called model analysis.

A few examples, where models may be used are ships in towing basins, air plane in wind tunnels. Hydraulic turbines, centrifugal pumps, spillways of dams, river channels etc. and to study such phenomenon as the action of waves and tides of the beaches, soil erosion and transportation of sediments.

It is defined as the similarity between the models and prototype in every respect, which means model and prototype have similar properties or model and prototype are completely similar.

There are basically three types of similitude are there, which are:

1. Geometric Similitude
2. Kinematic Similitude
3. Dynamic Similitude

Q4) Explain Geometric, Kinematic and dynamic similitude.

A4)

1. Geometric Similitude:

It is the similarity of shape. It is said to be exist between model and prototype if ratio of the entire corresponding linear dimension in the model and prototype are equal.

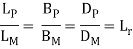
Where, Lp, Bp, and Dp are the length, breadth and diameter of prototype and Lm, Bm and Dm are the corresponding parameters of model.

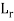=scale ratio

2.     Kinematic Similitude:

It is the similarity of motion. It is said to exist between model and prototype if ratio of velocity and acceleration at the corresponding points in model and prototype are equal.

Where, Vp1&Vp2 and ap1& ap2 are velocity and accelerations at point 1and 2 in prototype and Vm1& Vm2 and am1 & am2 are the velocity and acceleration in model.

3.     Dynamic Similitude:

It is the similarity of forces. It is said to exist between the model and prototype. If ratio of forces at the corresponding points in the model and prototype are equal.

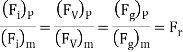
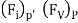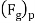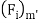
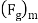Where and are inertia viscous and gravitational forces in prototype and and are inertia, viscous and gravitational forces in model,

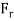is the Force ratio

Q5) Define Nusselt and Reynold number in dimensional analysis.

A5) 1. Nusselt number:

Average Nusselt number:

NuL = convective heat transfer /conductive heat transfer

= ℎ𝐿/𝑘

Where, L is the characteristic length, k is the thermal conductivity of the fluid, h is the convective heat transfer coefficient of the fluid.

Selection of the characteristic length should be in the direction of growth (or thickness) of the boundary layer; some examples of characteristic length are: the outer diameter of a cylinder in (external) cross flow (perpendicular to the cylinder axis), the length of a vertical plate undergoing natural convection, or the diameter of a sphere. For complex shapes, the length may be defined as the volume of the fluid body divided by the surface area.

The thermal conductivity of the fluid is typically (but not always) evaluated at the film temperature, which for engineering purposes may be calculated as the mean-average of the bulk fluid temperature T∞ and wall surface temperature Tw.

Local Nusselt number:

Nux = hxx/k

The length x is defined to be the distance from the surface boundary to the local point of interest.

2.Reynold Number: The Reynolds number is defined as the ratio of inertial forces to viscous forces and consequently quantifies the relative importance of these two types of forces for given flow conditions. The Reynolds number is defined below for each case.

Re = inertial forces/viscous forces

= ρ ∗ v ∗ L/μ = v ∗ L/ν

Where: v is the mean velocity of the object relative to the fluid (SI units: m/s)

L is a characteristic linear dimension, (travelled length of the fluid; hydraulic diameter when dealing with river systems) (m)

μ is the dynamic viscosity of the fluid (Pa·s or N·s/m² or kg/(m·s))

ν is the kinematic viscosity (ν = μ/ρ) (m²/s)

ρ is the density of the fluid (kg/m³).

Note that multiplying the Reynolds number by ρLv/ρLv yields ρv2L2/μvL, which is the ratio of the inertial forces to the viscous forces. It could also be considered the ratio of the total momentum transfer to the molecular momentum transfer.

While there is no theorem relating the non-dimensional Reynolds number (Re) to turbulence, flows at Reynolds numbers larger than 5000 are typically (but not necessarily) turbulent, while those at low Reynolds numbers usually remain laminar.

Q6) Described dimensionless numbers

A6) Dimensionless numbers or non-dimensional numbers are those which are useful to determine the flow characteristics of a fluid

Some important dimensionless numbers used in fluid mechanics and their importance is explained below.

Reynolds Number

Froude Number

Weber Number

Mach Number

Euler’s Number

1.Reynolds number is the ratio of inertia force to the viscous force. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems.

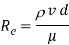
Where,

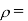Density of fluid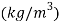

µ = viscosity of fluid (kg/m. s)

d = diameter of pipe (m)

v = velocity of flow (m/s)

2.Froude number- is the ratio of inertia force to the gravitational force. Froude number is significant in case of free surface flows where the gravitational force is predominant compared to other forces.

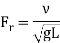
Where,

L = length of flow (m)

v = velocity of flow (m/s)

g = acceleration due to gravity (m/s2)

3.Weber number -is the ratio of inertia force to the surface tension. The formation of droplets or water bubbles in a fluid is normally due to surface tension. If Weber number is small, surface tension is larger and vice versa.

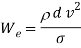
Where,

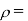Density of fluid

Surface tension of fluid (N/m)

d = diameter of water droplet (m)

v = velocity of flow (m/s)

4.Mach number -is the ratio of inertia force to the elastic force. If the Mach number is one, then the flow velocity is equal to the velocity of sound in the fluid. If it is less than one, then the flow is called subsonic flow, and if it is greater than one the flow is called supersonic flow.

Where,

v = Velocity of flow (m/s)

c = Velocity of sound in fluid (m/s)

5.Euler number - is the ratio of pressure force to the inertia force.

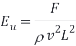
Where,

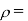Density of fluid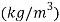

F = pressure force

L = Characteristic length of flow (m)

v = velocity of flow (m/s)

Q7) Define Mach number and Schmidt number.

A7) 1. Mach number:

In fluid mechanics, Mach number (M or Ma) is a dimensionless quantity representing the ratio of speed of an object moving through a fluid and the local speed of sound.

M = vobject/vsound

Where: M is the Mach number

vobject is the velocity of the source relative to the medium,

And vsound is the speed of sound in the medium.

2. Schmidt number:

Schmidt number (Sc) is a dimensionless number defined as the ratio of momentum diffusivity (viscosity) and mass diffusivity, and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes.

It is defined as:

Sc = ν/ D

= μ/ ρ ∗ D = viscous diffusion rate/molecular (mass) diffusion rate

Where: ν is the kinematic viscosity or (mu/rho) in units of (m²/s)

D is the mass diffusivity (m²/s).

μ is the dynamic viscosity of the fluid (Pa·s or N·s/m² or kg/m·s)

ρ is the density of the fluid (kg/m³).

The heat transfer analog of the Schmidt number is the Prandtl number.

Q8) Define Biot number and mention the application of these dimensionless numbers.

A8) The Biot number (Bi):

It is a dimensionless quantity used in heat transfer calculations. It gives a simple index of the ratio of the heat transfer resistances inside of and at the surface of a body. The Biot number is defined as:

Bi = h ∗ Lc /kb

Where: h = film coefficient or heat transfer coefficient or convective heat transfer coefficient

Lc = characteristic length, which is commonly defined as the volume of the body divided by the surface area of the body, such that

Lc = Vbody/ Asurface

Kb = Thermal conductivity of the body

Applications for dimensionless parameters:

1. To produce the ability for predicting the onset of turbulent flow is an important design tool for equipment such as piping systems or aircraft wings.

2. It is used scale the fluid dynamics problems and is used in scaling of fluid dynamics problems, and is used to determine dynamic similitude between two different cases of fluid flow.

3. It is used to predict the nature of the flow.

4. It is used for calculating momentum transfer in general and open channel flow and surface behaviour in particular.

5. These parameters are widely used while analyzing flow through spillways, weirs, channel flow, rivers and mostly in ship design.

Q9) Explain in brief the Buckingham Pi- theorem as method of dimensional analysis

A9) Buckingham’s Pi theorem:

Several methods can be used to form the dimensionless products, or pi term, that arises in a dimensional analysis.

Regardless of the method to be used to determine the dimensionless products, one begins by listing all (dimensional) variables that are known (or believed) to affect the given flow phenomenon.

Eight steps listed below outline a recommended procedure for determining the Π terms.

Steps 1: List all the variables.

List all the dimensional variables involved.

Keep the number of variables to a minimum, so that we can minimize the amount of laboratory work.

All variables must be independent. For example, if the cross -sectional area of a pipe is an important variable, either the area or the pipe diameter could be used, but not both not both, since they are obviously not independent.

Step 2: Express each of the variables in terms of in terms of basic dimensions and find the number of references the number of reference dimensions.

Step 3: Determine the required number of pi terms.

Let k be the number of variables in the problem.

Let r be the number of reference dimensions (primary dimensions) required to describe these variables.

The number of pi terms is k-r

Example: For pressure drop per unit length k=5, r = 3, the number of pi terms is k-r=5-3=2.

Step 4: Select number of repeating variables, where the number required is equal to the number of reference dimensions.

Step 5: Form a pi terms by multiplying one of the non-repeating variables by the product of the repeating variables, each raised to an exponent that will make the combination dimensionless.

Step 6: Repeat Step 5 for each of the remaining non-repeating variables.

Step 7: Check all the resulting pi terms to make sure they are dimensionless.

Step 8: Express the final form as a relationship among the pi terms, and think about what is means.

Q10) Calculate Reynolds number, if a fluid having viscosity of 0.4 Ns/m2 and relative density of 900 Kg/m3 through a pipe of 20 mm with a velocity of 2.5 m.

A10) Given that,

Viscosity of fluid μ

 μ=0.4Ns/ m2

Density of fluid ρ
ρ=900Kg/m2

Diameter of the fluid

L=20×10−3 m

Re=ρVL/μ

=900×2.5×20×10−3/0.4

=112.5

From the above answer, we observe that the Reynolds number value is less than 2000. Therefore, the flow of liquid is laminar.

Q11) Two parallel flat plates are immersed vertically in water. The clearance between the two plates is b. Calculate the elevation of the liquid due to capillary force. The surface tension, σ, and the density of water are 0.0725 N/m and 997 kg/m3, respectively. The contact angle, θc, is 50, and b ¼ 0.5 mm.

A11) Let the width of each plate be W.

The following force balance holds:

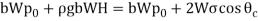
The height H is expressed as

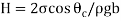
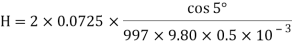
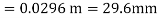
Q12) What is model analysis? Explain.

A12) For predicting the performance of the hydraulic structure such as dams or hydraulic machines such as turbines, before actually constructing and manufacturing, of the structures or machines are made and tests are conducted on them to obtain the desired information.

Model is small replica of the actual structure or machine.

The actual structure or machine is called as prototype. Models can be larger or smaller than the prototype.

Model analysis is an experimental method for finding the solutions of complex flow problems.

Following are the advantages of model analysis:

1. Using a dimensional analysis, a relationship between the variables influencing a flow problem is obtained which help in conducting test.
2. The performance of the hydraulic structure can be predicted in advance from its model.
3. The merits of the alternate design can be predicted with the help of model analysis to the most economical and safe design.

Q13) The power required by an agitator in a tank is a function of the following variables:

a. Diameter of the agitator

b. Number of rotations of the impeller per unit time

c. Viscosity of liquid

d. Density of liquid

(I) From dimensional analysis using Buckingham's method, obtain a relation between power and the four variables. (ii) The power consumption is found experimentally to be proportional to the square of the speed of rotation. By what factor would the power be expected to increase if the impeller diameter was doubled?

A13) f (P, D, N, p, µ) = O

Number of variables = 5

Number of dimensions = 3                              (i.e. M, L, T)

Number of dimensionless groups = 5-3 = 2

We need to choose the variables so as to represent the dimensions, and hence choose N, D and p Variable Dimensions

  N                                            [T-1]

  D                                            [L]

P                                             [ML -3]

In terms of dimensions, N = [T-I]

Therefore, [T] = N-l

Similarly, D = [L],

               [L] = D

               p = [ML -3],

           [M] = p[L3 ]

For the other variables:

The dimensions of power, P, is [ML 2 T -3]

Therefore, PM-1 L -2 T 3                          

Must be dimensionless

π1= P (pD3 ) -I (D)-2 (N -1)3

π1= P / pD3 D2 N3 = P / pD5 N3

The dimensions of µ is [ML -1 T-1]

Therefore,          µM-1 L T must be dimensionless

π2 = µ (p D3 ) -1 (D) (N-I) = µ (p-I D-3) (D) (N-I)

π2 = µ / pD2 N

Hence the relationship derived is,

P/ pD5 N 3 = k (µ / pD2 N)

Where N is any number which is constant

Part 2

Experimentally, it is shown that P ∞ N2

From the relationship, p = k (pD5 N 3 ) ( µ / D2 Np)n

From this relationship it can be seen that

P∞N3 N-n            or P∞N 3-n

But from the experiment, it was found that

P∞N2 Equating the experimental and theoretical findings,

                               3-n=2

Therefore n = 1

P= k (D5 N 3 p) (µ / D2 Np) = k (D3 N 2 µ)

p = k (D3 N2 µ)

The power required,

P1 = k (D13 N12 µ1)

In the second instance, when the size of agitator is doubled,

p = k (D23 N22 µ2)

In this case the viscosity and speed remain the same,

So µ1 = µ2 and N I = N2