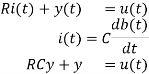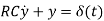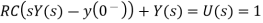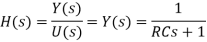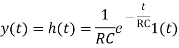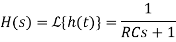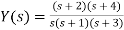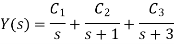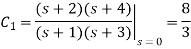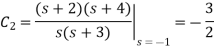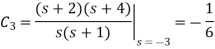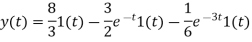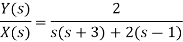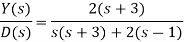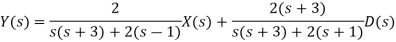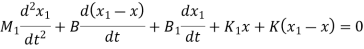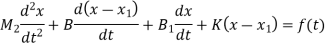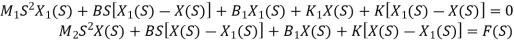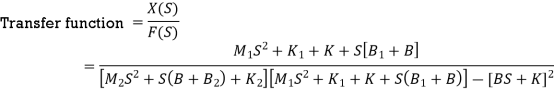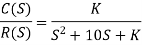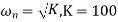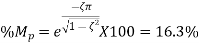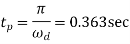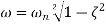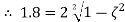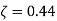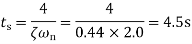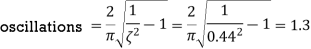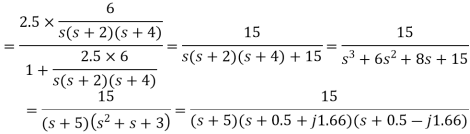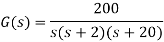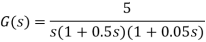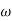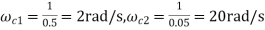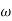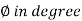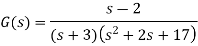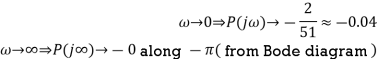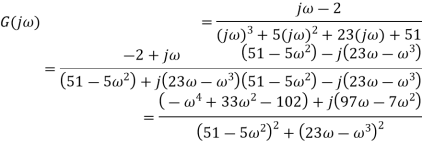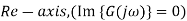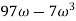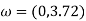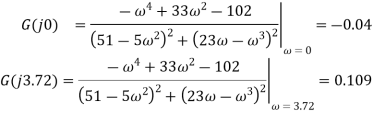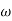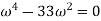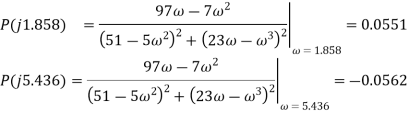undefined | unit 5 system models

Back to Study material

Instrumentation & Control

Unit-5

System model

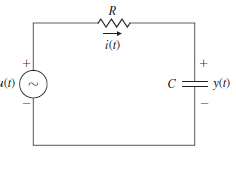
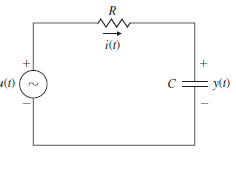
Q1) Compute the transfer function for the RC circuit driven by a voltage source as shown in Figure.

A1)

The system equation from Kirchhoff’s voltage law is

If the input voltage is a unit impulse signal

and we take the Laplace transform of both sides of the above equation

then assuming zero initial condition (y(0−) = 0) we find

The output, that is, the inverse Laplace transform of Y(s), is the impulse response

Therefore, the transfer function for this system is

Q2) Suppose you have find out .

find y(t)

A2) We may write Y(s) in terms of its partial-fraction expansion:

Using the cover-up method, we get

Taking laplace inverse of Y(s)

Q3) Determine the output Y(s) of the system shown in Figure when there is an input X(s) to the system as a whole and a disturbance signal D(s) at the point indicated.

A3)

If we set D(s) to zero output is given by

If we now set X(s) to zero This is a system with a forward path transfer function of 2/s and a positive feedback of (1/s+3) [-(s+1)]. This gives an output of

The total input is the sum of the outputs due to each of the inputs and so

Q4) Write the differential equations governing the mechanical translational system as shown in figure and determine the transfer function

A4)

Find equations for M1 and M2

Find Laplace transform equation for above equation

Solve the above equation and find transfer function

Q5) The unity feedback system is characterized by an open loop transfer function

G(s)=K/s(s+10)

Determine the gain K, so that the system will have a damping ratio of 0.5. For this value of K, determine settling time, peak overshoot and time to peak overshoot for a unit step input

A5) Given

G(s)=K/s(s+10) H(s)=1 𝜁=0.5

closed loop transfer function

We know

Percentage peak overshoot

Time to peak overshoot

Settling time

Q6) A second-order system has a natural angular frequency of 2.0 rad/s and a damped frequency of 1.8 rad/s. What are its

(a) damping factor, (b) 100% rise time, (c) percentage overshoot, (d) 2% settling time and (e) the number of oscillations within the 2% settling time?

A6) we know

The 2% settling time is given by

The number of oscillations occurring within the 2% settling time is given by

Q7) Determine whether the closed-loop control system described by Figure 10.15 is stable when G(s) = 6/[s(s+2)(s+4)] and K=2.5.

A7) For such a system with unit feedback-

The poles are thus located at s = -5, s = -0.5+j1.66 and s= -0.5- j1.66. All the poles are in the left half of the s-plane and so the system is stable.

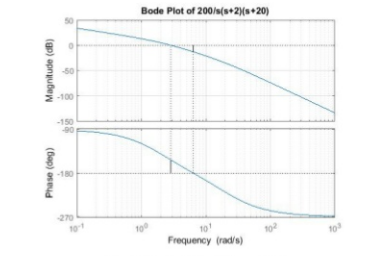
Q8) Sketch the asymptotic Bode plot for system having

G(s) =200/s(s+2)(s+20).

A8)

Step 1: Convert given transfer function into time-constant form

Step 2: Sinusoidal transfer function

Replace s with j

Step 3: Identify different parts of bode plot

Constant term: K = 5

Type of system: I. this means initial slope is -20 dB/dec, and intersection of the Mitial part of the plot with 0 dB axis occurs at = K = 5 rad/s

Corner frequencies

Step 4: Draw reference slopes on top left comer of the semi-log graph paper.

For magnitude plot draw a 0 dB axis line, with positive values above it like 20 dB. 40 dB etc. and negative values below it like -20 dB, 90 dB etc. For phase plot, draw a 180' axis line. Above it the values will be like -150,- 120, 90 etc. mid the values below it will be like - 210,-240°, -270 etc.

Step 5: Start plotting the magnitude plot by drawing a line with initial slope of - 20 413/dec that intersects the 0 dB axis at 5 rad/s. This slope continues till first corner frequency of 2 rad/s. Since this corner frequency is due to a pole, an additional slope of —20 dB/dec will be added. hence the slope now will be —40 dB/dec. This slope will added till second corner frequency of 20 rad/s. Since the second corner frequency IS also due to a pole, an additional slope of 20 dB/dec will be added, and hence the slope now will be —60 dB/dec. This slope will continue for all the further values of .