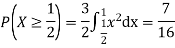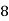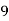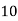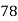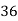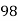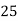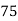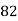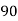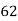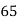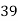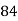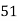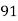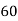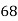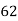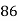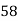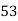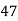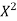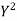Unit 2

Probability spaces

Q1: A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.

A1. We consider the following events:

A: Selected item comes from A.

B: Selected item comes from B.

D: Selected item is defective.

We are looking for 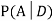. We know:

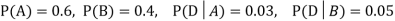
Now,

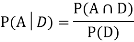
So we need

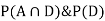
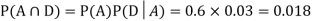
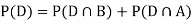
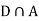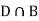Since, D is the union of the mutually exclusive events and (the entire sample space is the union of the mutually exclusive events A and B)

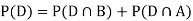
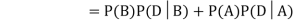
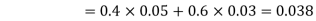
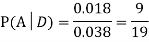
Q2. In a certain factory turning out razor blades there is a small chance of 0.002 of any need to be defective. The blades are supplied in packets of 10, use Poisson distribution to calculate the approximate number of packets containing no defective, one defective and to defective blades respectively in a consignment of 10000 packets.

A2. We know that m = no = 10 × 0.002=0.02

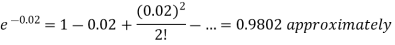
Probability of no defective blade is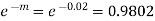

Therefore number of packets containing no defective blade is

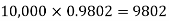
Similarly the number of packets containing one defective blade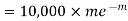

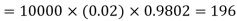
Find the number of packets containing to defective blades

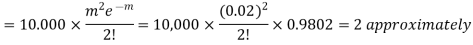
Q3. Fit a Poisson distribution to the set of observations:

A3. Mean =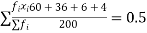

Therefore mean of Poisson distribution i.e. m =0.5

Hence the theoretical frequency for r successes is is

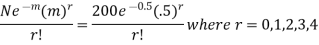
Therefore the theoretical frequencies are

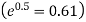
Q4. A box A contains 2 white and 4 Black balls. Another box B contains 5 white and 7 black balls. A ball is transferred from the box A to the box B. Then A ball is drawn from the box B. Find the probability that it is white.

A4. The probability of drawing a white ball from box B will depend on whether the transferred ball is black or white.

If black ball is transferred, it's probability is 4/6. There are now 5 white and 8 black balls in the box B.

Then the probability of drawing a white ball from box B is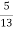

Thus the probability of drawing a white ball from B, if the transferred ball is black

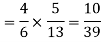
Similarly the probability of drawing a white ball from urn B if the transferred ball is white

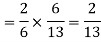
Hens required probability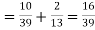

Q5. Two cards are selected at random from 10 cards numbered 1to10 find the probability p that the sum is odd if

The two cards are drawn together

the two cards are drawn one after the other without replacement

The two cards are drawn one after the other with replacement

A5. (i) two cars out of 10 can be selected in 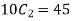ways. The sum is odd if one number is odd and other number is even. There being 5 odd numbers (1,3,5,7,9) and 5 even numbers (2,4,6,8,10) an what and an even number is chosen in 5×5=25 ways.

Thus,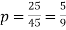

(ii)two cards out of 10 can be selected one of the other without replacing in 10 × 10 = 100 ways

An odd number is selected in 5 × 5 =25 ways and an even number in 5 × 5 = 25 ways

Thus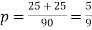

(iii)two cards can be selected one after the other with replacement in 10 × 10 =100 ways

An odd number is selected in 5 × 5 =25 ways and an even number in 5×5=25 ways

Thus,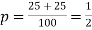

Q6. X is a continuous random variable with probability density function given by

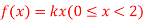
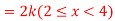
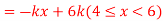
Find k and mean value of X.

A6. Since the total probability is unity.

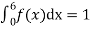
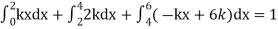
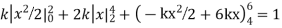
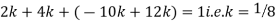
Mean of X =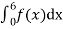

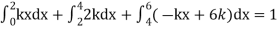
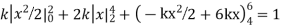
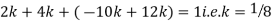
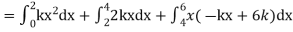
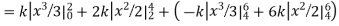
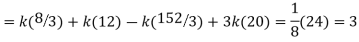
Q7: Ten students got the following percentage of marks in Economics and Statistics

Calculate the of correlation.

A7. Let the marks of two subjects be denoted by 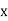and 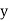respectively.

Then the mean for 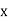marks 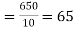and the mean ofy marks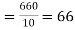

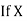and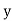 are deviations ofx’s and 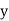’s from their respective means, then the data may be arranged in the following form:

Here,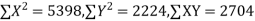

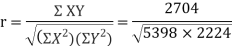
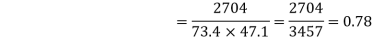
Q8: If X and Yare uncorrelated random variables, the of correlation between 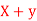and

A8.

Let 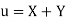and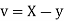

Then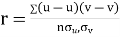

Now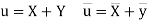

Similarly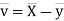

Now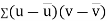

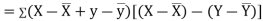
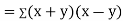
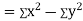
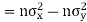
Also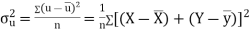

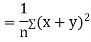
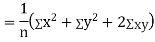
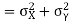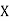(As and 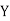are not correlated, we have )

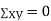Similarly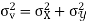

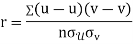
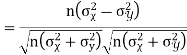
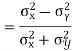
Q9. In a test on 2000 electric bulbs, it was found that the life of a particular make was normally distributed with an average life of 2040 hours and standard deviation of 60 hours. Estimated number of bulbs likely to burn for

(a)  More than 2150 hours

(b) Less than 1950 hours and

(c)  More than 1920 hours and but less than 2 160 hours

A9. Here μ = 2040 hours and 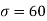hours

(a)  For x = 2150,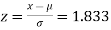

Area against z = 1.83 in the table III = 0.4664

We however require the area to the right of the ordinate at z = 1.83. This area = 0.5-0.4664=0.0336

Thus the number of bulbs expected to burn for more than 2150 hours.

 = 0.0336×2000 = 67 approximately

(b) For x = 1950,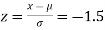

The area required in this case is to be left of z = -1.33

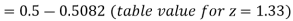
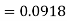
Therefore the number of bulbs expected to burn for less than 1950 hours

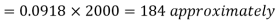
(c)  When x = 1920,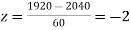

When x = 2160,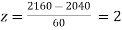

The number of bulbs expected to learn for more than 1920 hours but less than 2160 hours will be represented by the area between z = -2 and z = 2. This is twice the area from the table for z =2, i.e. 2 × 0.4772=0.9544

Thus required number of bulbs = 0.9544 × 2000 = 1909 nearly

Q10. Let X be a random variable with PDF given by

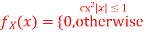
a, Find the constant c.

b. Find EX and Var (X).

c. Find P(X ).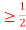

A10.

To find c, we can use

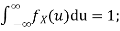
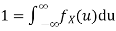
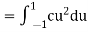
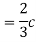
Thus we must have .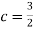

b.     To find EX we can write

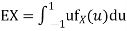
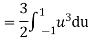
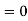
In fact, we could have guessed EX = 0 because the PDF is symmetric around x = 0. To find Variance (X) we have

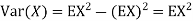
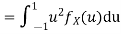
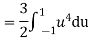
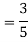
c.      To find 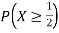we can write