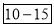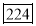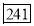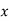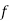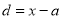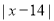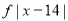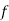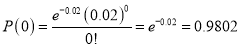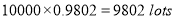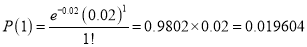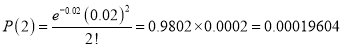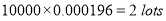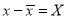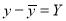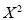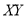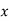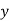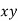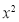UNIT 3
Basic Statistics
Q1: Find the value of Median from the following data.
No.of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
No.of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
A1. The given cumulative frequency distribution will first be converted into ordinary frequency as under
Class Interval | Cumulative frequency | Ordinary frequency |
0-5 5-10
15-20 20-25 25-35 30-35 35-40 40-45 | 29
465 582 634 644 650 653 655 | 29=29 224-29=195 465-224= 582-465=117 634-582=52 644-634=10 650-644=6 653-650=3 655-653=2 |
Median= size of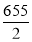 or 327.5th item
or 327.5th item
327.5th item lies in 10-15 which is the median class.
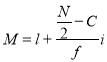
Where 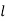 stands for lower limit of median class,
stands for lower limit of median class,
N stands for the total frequency,
C stands for the cumulative frequency just preceding the median class,
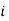 Stand’s for class interval
Stand’s for class interval
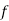 Stand’s for frequency for the median class.
Stand’s for frequency for the median class.
Median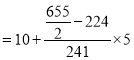

Q2: Find the mean deviation of the following frequency distribution.
Class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
Answer:
Let 
Class | Mid value
| Frequency
|
|
|
|
|
0-6 6-12 12-18 18-24 24-30 | 3 9 15 21 27 | 8 10 12 9 5 | -12 -6 0 6 12 | -96 -60 0 54 60 | 11 5 1 7 13 | 88 50 12 63 65 |
Total |
| 44 |
| -42 |
| 278 |
Mean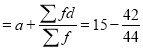
Average deviation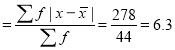
Q3:
Calculate the median, quartiles and the quartile coefficient of Skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 |
No. of Persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
A3.
Here total frequency .
.
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 |
| 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
| 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now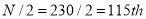 item which lies in 110-120 group.
item which lies in 110-120 group.
 Median or
Median or 
Also 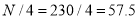 i.e.
i.e. 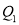 is
is 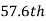 or
or  item which lies in 90-100 group.
item which lies in 90-100 group.
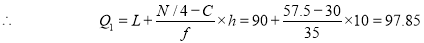
Similarly, 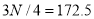 i.e.,
i.e.,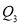 is
is 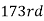 item which lies in 120-130 group.
item which lies in 120-130 group.
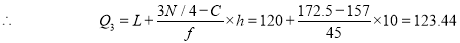
Hence quartile coefficient of skewness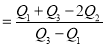
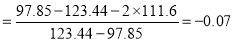 (approx.)
(approx.)
Q4: The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 item, now 60, at least 7 will live to be 70?
A4.
The probability that a man aged 60 will live to be 70
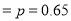
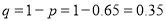
Number of men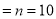
Probability that at least 7 men will live to
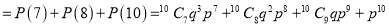
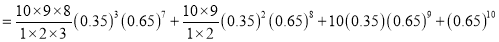
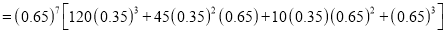
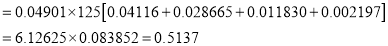
Q5: In a certain factory producing cycle tyres there is a small chance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution calculate the approximate number of lots containing no defective, one defective and two defective tyres, respectively, in a consignment of 10000 lots.
Answer:
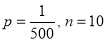
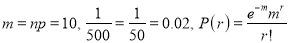
S.No | Probability of defective | Number of lots containing defective |
1 |
|
|
2 |
|
|
3 |
|
|
Question 6: Find the area under the normal curve in each of the cases.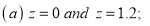
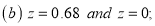
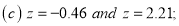
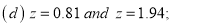
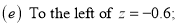
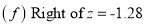
A6.
(a) Area between 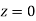 and
and 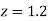 (b) Area between
(b) Area between 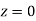 and
and 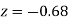
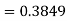
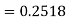
(c) Required area  (Area between
(Area between  and
and 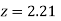 )+
)+
(Area between 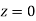 and
and  )
)
=(Area between 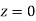 and
and 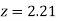 )
)
+(Area between 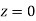 and
and 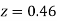 )
)
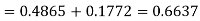
(d) Required area 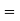 (Area between
(Area between 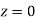 and
and 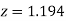 ) – (Area between
) – (Area between 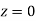 and
and  )
)
(e) Required area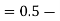 (Area between
(Area between  and
and 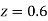 )
)
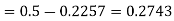
(f) Required area = (Area between 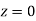 and
and 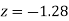 )
)
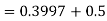
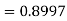
Q7:Psychological tests of intelligence and of engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and engineering ratio (E.R). Calculate the co-efficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R | 105 | 104 | 102 | 101 | 99 | 98 | 96 | 92 | 93 | 92 |
E.R | 101 | 103 | 100 | 98 | 96 | 104 | 92 | 94 | 97 | 94 |
A7. We construct the following table:
Student | Intelligence ratio
| Engineering ratio |
|
|
|
A B C D E F G H I J | 100 6 104 5 102 3 101 2 100 1 99 0 98 -1 96 -3 93 -6 92 -7 | 101 3 103 5 100 2 98 0 95 -3 96 -2 104 6 92 -6 97 -1 94 -4 | 36 25 9 4 1 0 1 9 36 49 | 9 25 4 0 9 4 36 36 1 16 | 18 25 6 0 -3 0 -6 18 6 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of 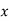 i.e.,
i.e.,  and mean of
and mean of 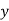 , i.e.,
, i.e., 
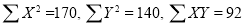
Substituting these values in the formula (1), we have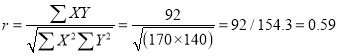
Q8: In a partially destroyed laboratory record, only the lines of regression of y on x and x on y are available as 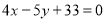 and
and 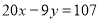 respectively. Calculate
respectively. Calculate 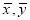 and the coefficient of correlation between x and y.
and the coefficient of correlation between x and y.
A8. Since the regression lines pass through , therefore,
, therefore,
 ,
, 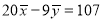
Solving these equations, we get 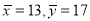
Rewriting the line of regression of y on x as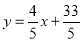 , we get
, we get
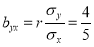 …. (i)
…. (i)
Rewriting the line of regression of x on y as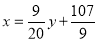 , we get
, we get
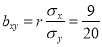 …. (ii)
…. (ii)
Multiplying (i) and (ii), we get
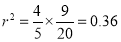
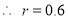
Hence 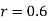 , the positive sign being taken as
, the positive sign being taken as 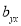 and
and 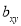 both are positive.
both are positive.
Q9: Find the best values of a and b so that 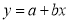 fits the data given in the table.
fits the data given in the table.
X | 0 | 1 | 2 | 3 | 4 |
Y | 1 | 2.9 | 4.8 | 6.7 | 8.6 |
A9. 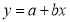
|
|
|
|
0 | 1 | 0 | 0 |
1 | 2.9 | 2.9 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
| |
|
|
Normal equations 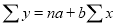 …. (2)
…. (2)
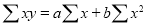 …. (3)
…. (3)
On putting the values of 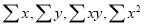 in (2) and (3), we have
in (2) and (3), we have
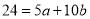 …. (4)
…. (4)
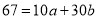 …. (5)
…. (5)
On solving (4) and (5), we get
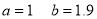
On Substituting the values of a and b in (1), we get

Q10: A certain stimulus administered to each 12 patients resulted in the following increases of blood pressure: 5, 2. 8, -1, 3, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure.
A10. Let us assume that the stimulus administered to all the 12 patients will increase the B.P. Taking the population to be normal with mean 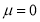 and S.D.
and S.D.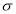 ,
,
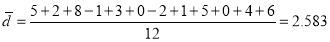
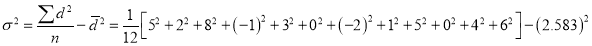

Now 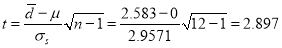
Here 
For 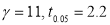 , from table IV.
, from table IV.
Since the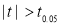 , our assumption is rejected i.e., the stimulus does not increase the B.P.
, our assumption is rejected i.e., the stimulus does not increase the B.P.