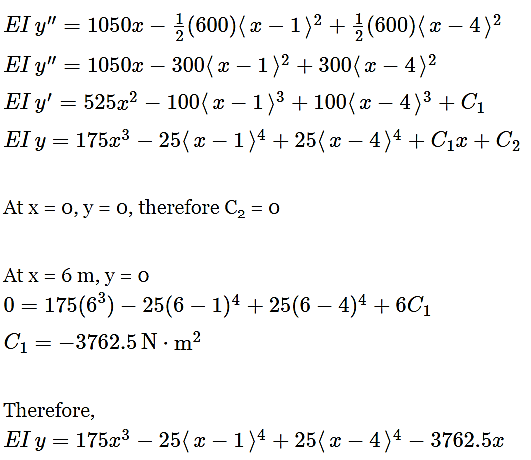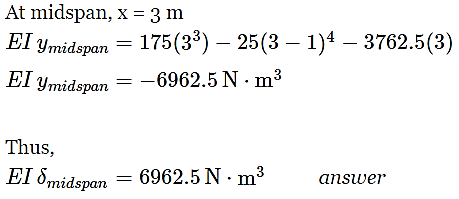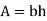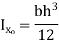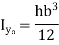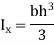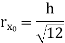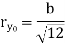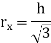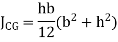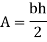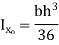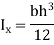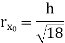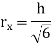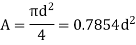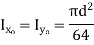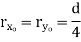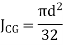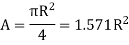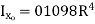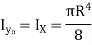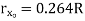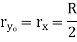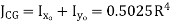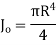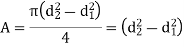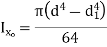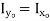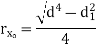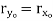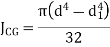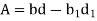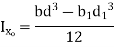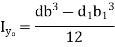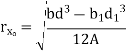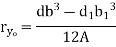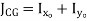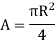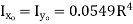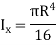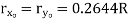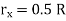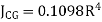Unit – 3

Moment of Inertia about an axis and polar moment of inertia

Question 1: Prepare a chart of Moment of inertia about an axis and polar moment of inertia for different shapes.

Answer:

Question 2: Describe Deflection of beam using double integration method.

Answer:  Assumption: The following assumptions are undertaken in order to derive a differential equation of elastic curve for the loaded beam

1. Stress is proportional to strain i.e., hooks law applies. Thus, the equation is valid only for beams that are not stressed beyond the elastic limit.

2. The curvature is always small.

3. Any deflection resulting from the shear deformation of the material or shear stresses is neglected.

It can be shown that the deflections due to shear deformations are usually small and hence can be ignored.

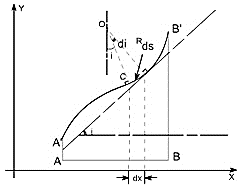
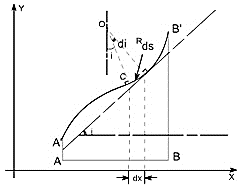
Consider a beam AB which is initially straight and horizontal when unloaded. If under the action of loads the beam deflect to a position A’B’ under load or infact we say that the axis of the beam bends to a shape A’B’. It is customary to call A’B’ the curved axis of the beam as the elastic line or deflection curve.

In the case of a beam bent by transverse loads acting in a plane of symmetry, the bending moment M varies along the length of the beam and we represent the variation of bending moment in B.M diagram. Further, it is assumed that the simple bending theory equation holds good.

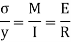
If we look at the elastic line or the deflection curve, this is obvious that the curvature at every point is different; hence the slope is different at different points.

To express the deflected shape of the beam in rectangular co-ordinates let us take two axes x and y, x-axis coincide with the original straight axis of the beam and the y - axis shows the deflection.

Further, let us consider an element ds of the deflected beam. At the ends of this element let us construct the normal which intersect at point O denoting the angle between these two normal.

But for the deflected shape of the beam the slope is at any point C is defined,

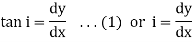
Assuming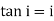

Further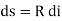

However,

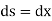[usually for small curvature]

Hence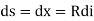

or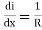

substituting the value of i, on get

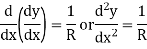
From the simple bending theory

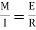or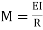

So the basic differentials equation governing the deflection of beams is

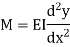
This is the differential equation of the elastic line for a beam subjected to bending in the plane of symmetry. Its solution y = f(x) defines the shape of the elastic line or the deflection curve as it is frequently called.

The governing differential equation is defined as

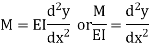
On integrating one get,

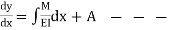this equation gives the slope of the loaded beam.

Integrate once again to get the deflection.

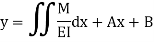
Where A and B are constants of integration to be evaluated from the known conditions of slope and deflections for the particular value of x.

Question 3: Derive equation for Cantilever Beam with Concentrated Load at the end.

Answer:

Consider any X-section X-X located at a distance x from the left end or the reference, and write down the expressions for the shear force and the bending moment.

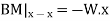
Therefore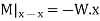

The governing equation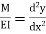

Substituting the value of M in terms of x then integrating the equation one get

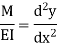
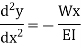
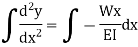
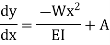
Integrating once more,

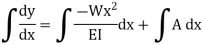
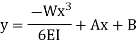
The constants A and B are required to be found out by utilizing the boundary conditions as defined below

i.e at x= L ; y= 0          ——————– (1)

at x = L ;dy/dx = 0      ——————– (2)

Utilizing the second condition, the value of constant A is obtained as

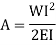
While employing the first condition yields

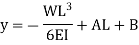
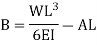
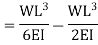
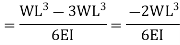
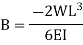
Substituting the values of A and B we get

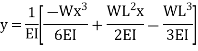
The slope as well as the deflection would be

Maximum at the free end hence putting 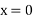we get,

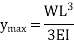
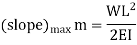
Question 3: Derive the equation for Cantilever with Uniformly distributed Loads.

Answer: 

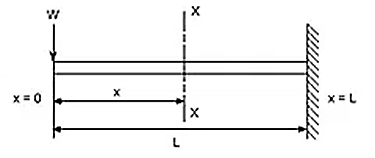
Consider any X-section X-X located at a distance x from the left end or the reference, and write down the expressions for the shear force and the bending moment.

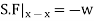
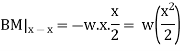
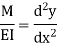
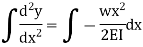
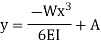
Integrating once more,

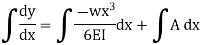
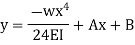
Boundary conditions relevant to the problem are as follows:

1. At x = L; y = 0

2. At x= L; dy/dx = 0

The second boundary conditions yield

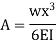
Whereas the first boundary conditions yields

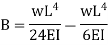
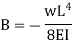
Thus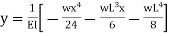

So 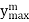will be at x=0

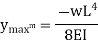
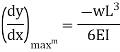
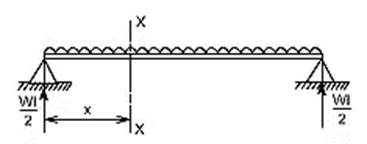
Question 4: Derive expression for Simply Supported beam with uniformly distributed Loads.

Answer:

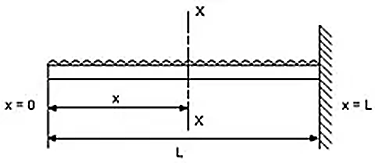
In order to write down the expression for bending moment consider any cross-section at distance of x metre from left end support.

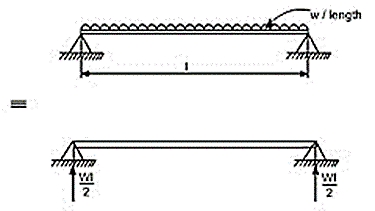
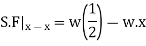
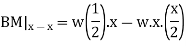
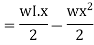
The differential equation which gives the elastic curve for the deflected beam is

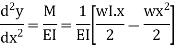
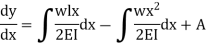
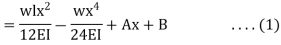
Boundary conditions which are relevant in this case are that the deflection at each support must be zero.

i.e., at x = 0; y = 0: at x = l; y = 0

let us apply these two boundary conditions on equation (1) because the boundary conditions are on y, this yields B = 0.

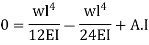
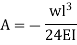
So the equation which gives the deflection curve is

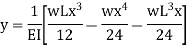
In this case the maximum deflection will occur at the center of the beam where x = L/2 [ i.e., at the position where the load is being applied.] So, if we substitute the value of x = L/2.

Then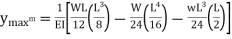

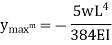
Question 5: Determine the maximum deflection δ in a simply supported beam of length L carrying a concentrated load P at midspan.

Answer:

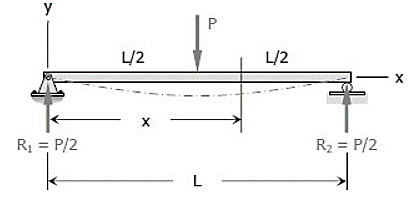
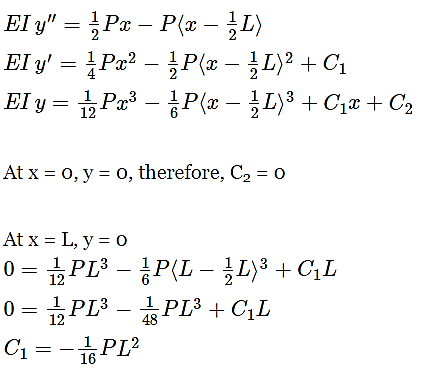
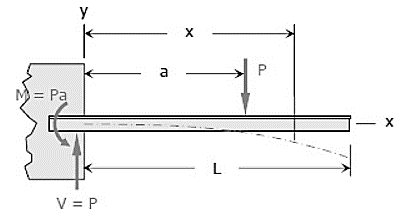
Question 6: Determine the maximum value of EIy for the cantilever beam loaded as shown in Fig. Take the origin at the wall.

Answer:

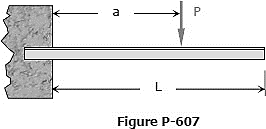
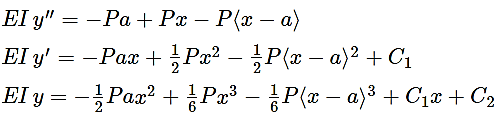
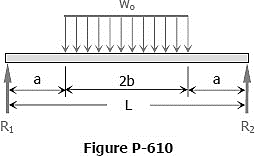
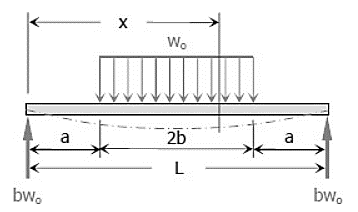
Question 7: The simply supported beam shown in Fig.carries a uniform load of intensity wo symmetrically distributed over part of its length. Determine the maximum deflection δ.

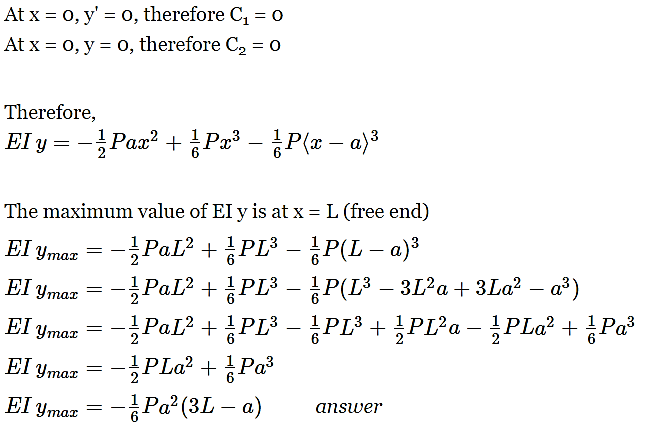
Answer:

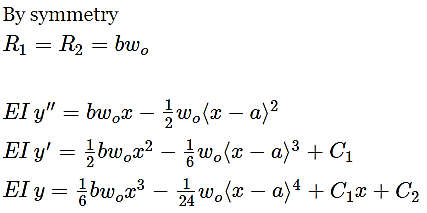
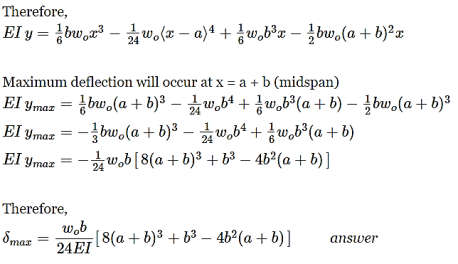
Question 8: Compute the value of EI δ at midspan for the beam loaded as shown in fig. If E = 10 GPa, what value of I is required to limit the midspan deflection to 1/360 of the span?

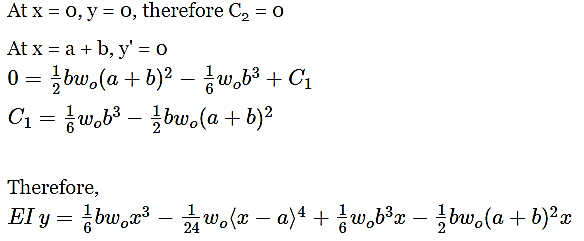
Answer:

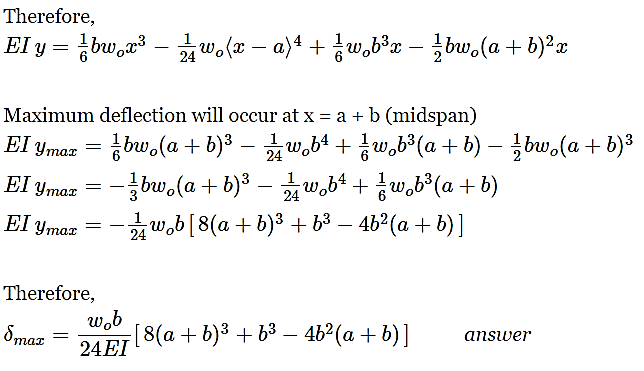
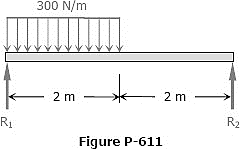
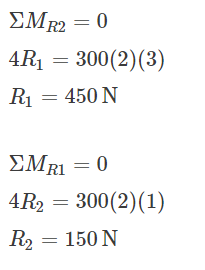
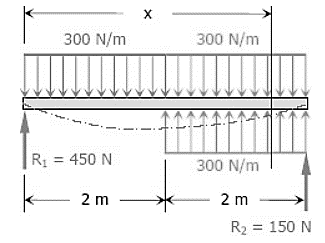
Question 9: Compute the midspan value of EI δ for the beam loaded as shown in Fig.

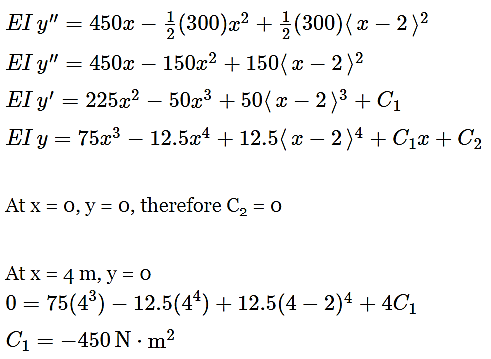
Answer:

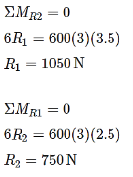
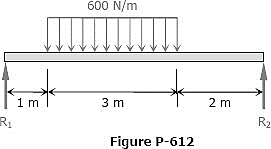
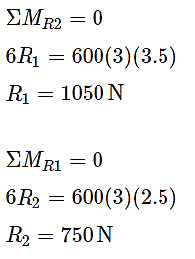
Question 10: For the beam loaded as shown in Fig., calculate the slope of the elastic curve over the right support.

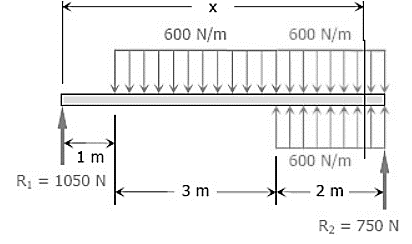
Answer: