Unit 4
First Law for Flow Processes
Q1. Derive an expression for First law of thermodynamics applied to control volume.
A1. First law of thermodynamics applied to control volume:
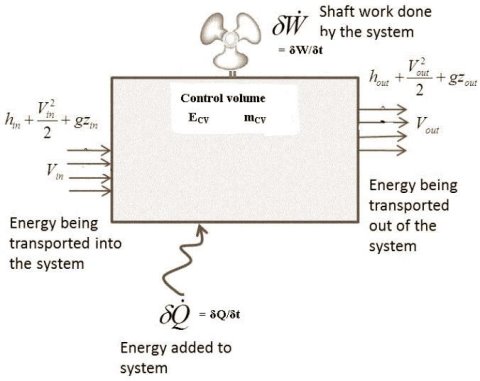
As shown in the diagram above, consider the control volume having inflow of energy.
The system is producing some shaft work as shown in the figure.
There is a continuous influx and outflux of the fluid in the system.
The rate of heat energy addition to the control volume = δQ/δt
The rate of work energy providing by control volume to the surrounding = δW/δt.
The mass flow rate entering to the control volume = dm1/dt
The mass flow rate leaving the control volume =dm2/dt
Rate of change of mass in control volume = dmCV/dt
According to principle of conservation of mass, we will have following equation
(Mass flow rate entering to the system) - (Mass flow rate leaving the system) = Rate of change of mass in control volume
(dm1/dt) - (dm2/dt) = dmCV/dt
E = u + pv + V2/2 + gz
E = h + V2/2 + gz
Ein = hin + V2in/2 + gzin = h1 + V21/2 + gz1
E1 = h1 + V21/2 + gz1
Eout = hout + V2out/2 + gzout = h2 + V22/2 + gz2
E2 = h2 + V22/2 + gz2
Q2. What is a Steady flow system?
A2. Steady Flow System -
Defined as the system in which the mass flow rate into the system is equal to mass flow rate out of the system.
Mass flow rate in m1 = Mass flow rate out, m2 = constant = m
Consider the flow of fluid through a pipe of cross-sectional area A,
specific volume V, at Velocity C.
volume flow rate = A (m2) × C (m/s)
Mass flow rate m (kg/s) = Volume flow rate / Specific volume
m =AC/V = ρAC= Continuity Equation
Q3. What are the assumptions of stead flow systems?
A3. Assumptions-
Q4. Derive SFEE on time basis.
A4. S.F.E.E. on unit time basis -
Total energy flow rate into the control = total energy flow rate out of control volume.
Q+ m [Internal energy + Flow work + KE + PE ]1 = W +m [Internal energy + Flow work + KE + PE]2
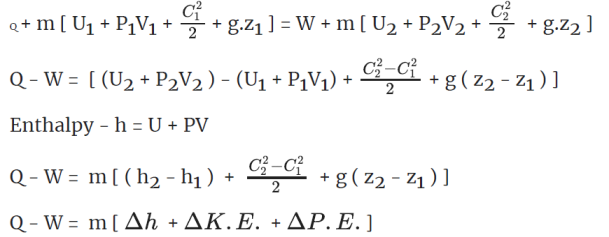
Q5. Derive an expression for applying SFEE to a boiler.
A5. Boiler - A boiler is a device used for steam generation at constant pressure.
Heat is supplied to boiler drum externally by combustion of fuel in presence of air. Products of combustion are called Flue gases.
For a boiler - W =0, ΔK.E.=0 and Δ P.E.=0
On using these conditions S.F.E.Equation,
Q = m (h2 - h1)
Q6. Derive an expression for applying SFEE to a condenser.
A6. Condenser -
A condenser is a device used for steam condensation at constant pressure.
For a condenser - W =0, ΔK.E.=0 and Δ P.E.=0
On using these conditions S.F.E.Equation,
Q = m (h1 – h2)
Q7. Derive an expression for applying SFEE to a nozzle.
A7. Nozzle: In case of a nozzle as the enthalpy of the fluid decreases and pressure drops simultaneously the flow of fluid is accelerated. This is generally used to convert the part of the energy of steam into kinetic energy of steam supplied to the turbine.
For this system, ∆PE=0, W=0, Q=0
Applying the energy equation to the system,
h1+(C12/2 )= h2+(C22/2) h1+(C12/2) = h2+(C22/2)
Q8. Derive an expression for applying SFEE to a turbine.
A8.
Turbine: In a steam or gas turbine steam or gas is passed through the turbine and part of its energy is converted into work in the turbine. This output of the turbine runs a generator to produce electricity. The steam or gas leaves the turbine at lower pressure or temperature.
Applying energy equation to the system,
Here, Z1=Z2
h1+(C12/2) −Q=h2+(C22/2) +W
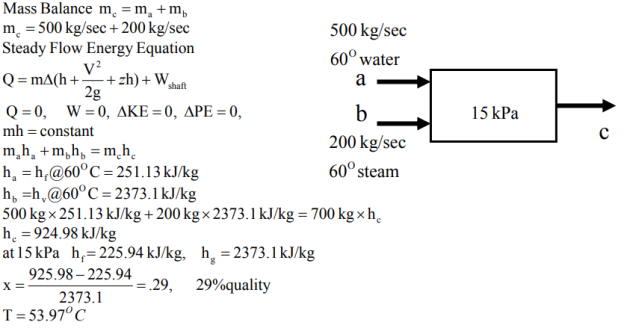
Q9. 500 kg/sec of 60 ℃ water is mixed with 200 kg/sec 60 ℃ saturated steam in a tank at a pressure of 15kPa. What are the exit conditions?
A9.
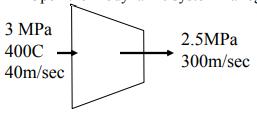
Q10. Steam at 3MPa and 400 ℃ enters an adiabatic nozzle steadily with a velocity of 40 m/sec and leaves at 2.5 MPa and 300 m/sec.
Determine:
(a) the exit temperature and
(b) the ratio of inlet to exit area.
A10. Open thermodynamic system - a region in space

h1 & v1 = superheat @ (T = 400 ℃, P = 3 MPa)
h1 = 3231.7 kJ/kg
V1 = 0.09938 m³ /kg
Applying SFEE,
We get, h1 + v12 / 2 = h2 + v22 / 2
∴ h2 = h1 + {(v12 - v22)/ 2}
Substituting the above found values from the steam tables and given data,
h2 = 3187.5 kJ/kg
T2 @ (h = 3187.5, p = 2.5)
T2 = 376.5 ℃
v2 @ (h = 3187.5, p = 2.5)
v = 0.11626 m³ /kg
b. m = ρAV
A1 V1 / v1 = A2 V2 / v2
Substituting the given and above found values,
A2 / A1 = 0.1872