Unit - 3
Design of Power Screws
Q1) What is Power Screw?
A1)
A power screw is a mechanical device for conveying power and turning rotary motion into linear motion. A translation screw is another name for a power screw. Rather than clamping the machine components, it uses helical translatory motion of the screw thread to convey power. The following are the major applications of power screws:
- Raising the load, e.g., screw-jack.
- Obtaining correct motion in machining operations, e.g., lathe leadscrew.
- Clamping a work piece, e.g., vice; and
- Loading a specimen, e.g., universal testing machine.
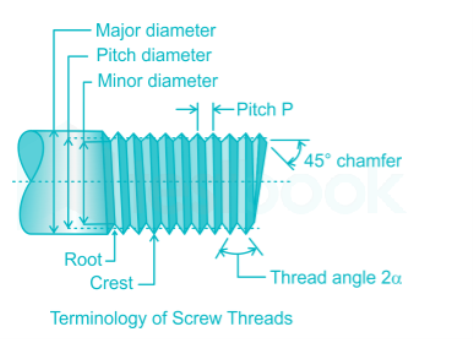
Q2) Define Pitch, Lead, Nominal Diameter, Core Diameter & Angle of Helix
A2)
- Pitch
Pitch is defined as the distance between a point on one thread and the matching point on the neighbouring thread measured parallel to the screw's axis. The letter p stands for it.
- Lead
The lead is defined as the distance measured parallel to the screw's axis that the nut will advance in one screw revolution. The letter l stands for it. The lead of a single-threaded screw is the same as the pitch. The lead on a double-threaded screw is twice the pitch, and so on.
- Nominal diameter
The nominal diameter is the screw's largest diameter. It's also known as the major diameter. The letter d stands for it.
- Core Diameter
The screw thread's core diameter is the smallest diameter. It's also known as a minor diameter. The letters de designate it.
- Angle of the Helix
The helix angle is defined as the angle formed by the thread's helix and a plane perpendicular to the screw's axis. The lead and the screw's mean diameter are connected to the helix angle. It's also known as the lead angle. The helix angle is represented by the letter α.
Q3) Explain Differential Screws.
A3)
A differential screw is a mechanical device that consists of two screws in series that are positioned so that the resultant motion is the difference of the two screws' separate motions. With the help of Fig, the differential screw principle is explained. The composite screw is made up of two parts: the larger S, which has a pitch of 4 mm, and the smaller S2, which has a pitch of 3 mm. Both threads have the same helix hand, as they are both right-handed. S passes through the frame F in its larger form. On the smaller section S2, there is a square nut N. As seen in Fig., the nut cannot rotate and can only glide in an axial direction with regard to the frame. When viewed from the right side, the handle rotates one revolution in the clockwise direction. When the fingers are retained in the direction of rotation, the thumb indicates the direction of movement of the screw, according to the right-hand thumb rule. The nut's movement is in the opposite direction as the screws. With relation to the frame, the screw S will move 4 mm to the left. In relation to the frame, the nut N will move 3 mm to the right. The nut will move (4-3) mm to the left in relation to the frame as a result of this action. If the pitches of two screws are p1 and p2, the resultant motion is equal to (P1-P2) or the difference of the motions.
Q4) Explain Compound Screws.
A4)
A compound screw is a mechanical device that consists of two screws connected in series, with the resultant motion equal to the sum of the two screws' individual motions. Figure 1 depicts a compound screw. Except for the hand of helix for the two screws, the configuration is similar to that of a differential screw. The bigger section S has right-handed threads, whereas the smaller half S has left-handed threads. The consequent movement of the nut with respect to the frame may be proven to be (4 +3) mm to the left. If the pitches of two screws are p and p2, the resultant motion is equal to (p1 + p2), or the sum of the individual motions.
Q5) Explain Recirculating Ball screw
A5)
A recirculating ball screw is made up of a screw and a nut with a sequence of balls between their surfaces. Instead of having square or trapezoidal thread profiles, the screw and nut feature approximately semi-circular thread profiles. The balls progress in the grooves of the nut and screw when the screw is spun. They are gathered and returned at the conclusion of the nut. Ball bearing screw or simply ball screw are other names for the recirculating ball screw. Because backlash is eliminated, such screws are preloaded and provide precise motion. Because of the little friction, no heat is generated. High speeds of up to 10 m/min can be achieved using recirculating ball screws. Contact stresses are applied to the balls, screw, and nut. They're normally constructed of nickel chromium steel that's been heat treated to a hardness of 58 to 65 HRC on the surface.
Q6) Write Recirculating Ball screw applications.
A6)
- Automobile steering gears
- Power actuators
- X-Y recorders of CNC machines
- Aircraft landing gear retractors
- Hospital bed adjustors
- Machine tool controls
Q7) Explain square thread
A7)
A square thread is designed to transmit power in either direction. This thread has the highest efficiency and the lowest radial or bursting pressure on the nut. Cutting with taps and dies is difficult. It is typically cut on a lathe with a single point tool, and wear is difficult to compensate for. Screw jacks, presses, and clamping devices all use square threads.
Q8) Explain Acme or trapezoidal threads
A8)
Acme or trapezoidal threads are variations on square threads. The slight inclination of its sides reduces the efficiency slightly more than a square thread and introduces some bursting pressure on the nut, but it increases its area in shear. It is used where a split nut is required and where provision is made for wear, such as in a lathe's lead screw. Wear can be compensated for with an adjustable split nut. Acme thread can be cut with dies, making it more easily manufactured than square thread.
Q9) Explain buttress thread.
A9)
Buttress threads are used when large forces act in only one direction along the screw axis. This thread combines the higher efficiency of square thread with the acme thread's ease of cutting and adaptability to a split nut. Because of the greater thickness at the base of the thread, it is stronger than other threads. The buttress thread is only used for a limited amount of power transmission. It is used as a thread for jack screws and vices.
Q10) A vertical screw with single start square threads of 50 mm mean diameter and 12.5 mm pitch is raised against a load of 10 kN using a hand wheel with a threaded boss that acts as a nut. The axial load is carried by a thrust collar with a mean diameter of 60 mm that supports the wheel boss. The screw has a coefficient of friction of 0.15 and the collar has a coefficient of friction of 0.18. Find a suitable diameter of the hand wheel if the tangential force applied by each hand to the wheel is 100 N.
A10)
Given: d = 50 mm; p = 12.5 mm; W = 10 kN = 10 × 103N; D = 60 mm or R = 30 mm; μ = tan φ = 0.15; μ1 = 0.18; P1 = 100 N
We know that 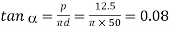
And the tangential force required at the circumference of the screw,
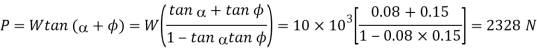
We also know that the total torque required to turn the had wheel,
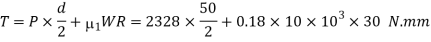
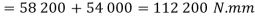
 Diameter of the hand wheel in mm.
Diameter of the hand wheel in mm.
We know that the torque applied to the handwheel,
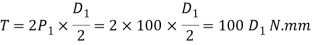
D1 = 112 200 / 100 = 1122 mm = 1.122 m
Q11) An electric motor driven power screw moves a nut in a horizontal plane against a force of 75 kN at a speed of 300 mm / min. The screw has a single square thread of 6 mm pitch on a major diameter of 40 mm. The coefficient of friction at screw threads is 0.1. Estimate power of the motor.
A11)
Given 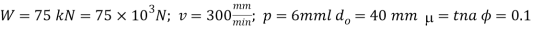
We know that mean diameter of the screw 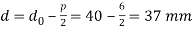
And 
We know that tangential force required at the circumference of the screw
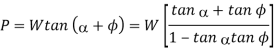
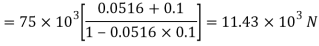
And torque required to operate the screw 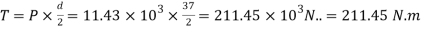
Since the screw moves in a nut at a speed of 300 mm/min and the pitch of the screw is 6 mm, therefore speed of the screw in revolutions per minute (r.p.m)
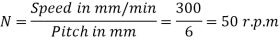
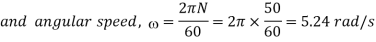
 the motor =T =211.45×5.24=1108 W=1.108 kW
the motor =T =211.45×5.24=1108 W=1.108 kW
Q12) The cutter of a broaching machine is pulled by square threaded screw of 55 mm external diameter and 10 mm pitch. The operating nut takes the axial load of 400 N on a flat surface of 60 mm and 90 mm internal and external diameters respectively. If the coefficient of friction is 0.15 for all contact surfaces on the nut, determine the power required to rotate the operating nut when the cutting speed is 6 m/min. Also find the efficiency of the screw.
A12)
Given: do = 55 mm; p = 10 mm = 0.01 m; W = 400 N; D2 = 60 mm or R2 = 30 mm; D1 = 90 mm or R1 = 45 mm; μ = tan φ = μ1 = 0.15; Cutting speed = 6 m / min
Power required to operate the nut
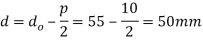
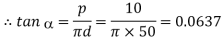
And force required at the circumference of the screw,
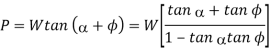

We know that means radius of the flat surface
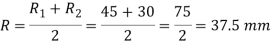
∴Total torque required
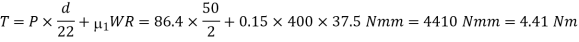
We know that speed of the screw,
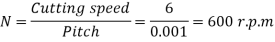
And angular speed, =2πN/60=2π×600/60=62.84 rad/s
∴ Power required to operate the nut
=T =4.41×62.84=277W=0.277kW
Efficiency of the screw
We know that the Efficiency of the screw
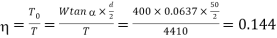 or 14.4%
or 14.4%
Q13) A vertical two-start square threaded screw with a mean diameter of 100 mm and a pitch of 20 mm can withstand an 18 kN vertical load. A collar bearing with an outside diameter of 250 mm and an inside diameter of 100 mm takes the axial thrust on the screw. Determine the force required at the end of a 400-mm-long lever to lift and lower a load. The coefficient of friction for the vertical screw and nut is 0.15, while the coefficient of friction for the collar bearing is 0.20.
A13)
Given: d = 100 mm; p = 20 mm; W = 18 kN = 18 × 103N; D1 = 250 mm or R1 = 125 mm; D2 = 100 mm or R2 = 50 mm; l = 400 mm; μ = tan φ = 0.15; μ1 = 0.20.
Force required at the end of lever
Let P=Force required at the end of lever
Since the screw is a two start threaded screw, therefore lead of the screw
=2p=2×20=40 mm
We know that 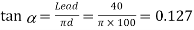
1. For raising the load
We know that tangential force required at the circumference of the screw,
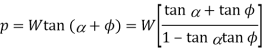
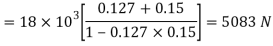
And mean radius of the collar,
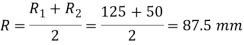
∴ Total torque at the end of lever
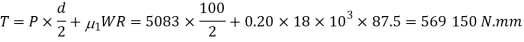
We know that torque required at the end of lever(T)
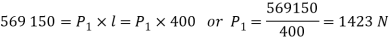
2. For lowering the load
We know that tangential force required at the circumference of the screw.
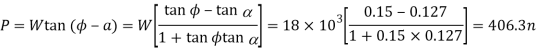
And the total torque required the end of lever,

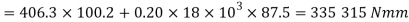
We know that torque required at the end of lever(T)
 Ans.
Ans.
Q14) The mean diameter of the square threaded screw having pitch of 10 mm is 50 mm. A load of 20 kN is lifted through a distance of 170 mm. Find the work done in lifting the load and the efficiency of the screw, when
1. The load rotates with the screw, and
2. The load rests on the loose head which does not rotate with the screw.
The external and internal diameter of the bearing surface of the loose head are 60 mm and 10 mm respectively. The coefficient of friction for the screw and the bearing surface may be taken as 0.08.
A14)
Given: p = 10 mm; d = 50 mm; W = 20 kN = 20 × 103 N; D1 = 60 mm or R2 = 30 mm; D2 = 10 mm or R2 = 5 mm; μ = tan φ = μ1 = 0.08
We know that 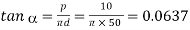
∴ Force required at the circumference of the screw to lift the load
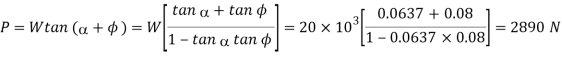
And required to overcome the friction
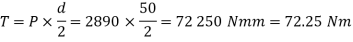
Since the load is lifted through a vertical distance of 170mm and the distance moved by the screw in one rotation is 10mm (equal to pitch), therefore number of rotations made by the screw
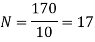
2. When the load does not rotate with the screw.
We know that mean radius of the bearing surface,
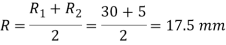
And torque required to overcome friction at the screw and the collar
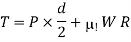
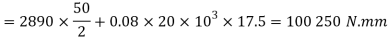
 Workdone by the torque in lifting the load
Workdone by the torque in lifting the load
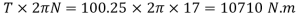
We know the torque required to lift the load, neglecting friction,
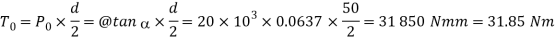
∴ Efficiency of the screw
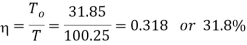
Q15) A lathe's lead screw has Acme threads with an outside diameter of 50 mm and a pitch of 8 mm. To drive the tool carriage, the screw must exert an axial force of 2500 N. The thrust is carried by a collar with dimensions of 110 mm outside diameter and 55 mm inside diameter, and the lead screw rotates at 30 revolutions per minute. Determine (a) the power required to drive the screw and (b) the lead screw's efficiency. Assume the screw has a coefficient of friction of 0.15 and the collar has a coefficient of friction of 0.12.
A15)
Given: do = 50 mm; p = 8 mm; W = 2500 N; D1 = 110 mm or R1 = 55 mm; D2 = 55 mm or R2 = 27.5 mm; N = 30 r.p.m.; μ = tan φ = 0.15; μ2 = 0.1
(a) Power required to drive the screw
We know that mean diameter of the screw
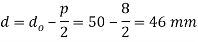
Since the angle for Acme threads is 2=29 or =14.5
or =14.5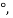 therefore vortual coefficient of friciton
therefore vortual coefficient of friciton
∴ 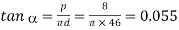
We know that the force required to overcome friction at the screw,
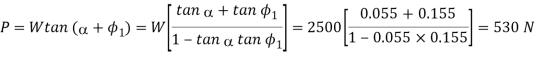
∴And torque required to overcome friction at the screw.
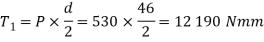
We know that mean radius of collar,
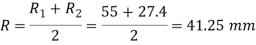
Assuming uniform wear, the torque required to overcome friction at collars,
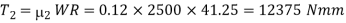
∴ Total torque required to overcome friction,
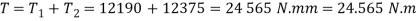
We know that power required to drive the screw
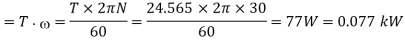
(b) Efficiency of the lead screw
We know that the torque required to drive the screw with no friction.
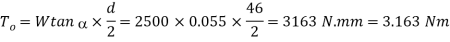
Efficiency of the lead screw

Q16) A vertical two-start square threaded screw with a mean diameter of 100 mm and a pitch of 20 mm can withstand a vertical load of 18 kN. The screw's nut is installed in the hub of an 80-toothed gear wheel that meshes with a 20-toothed pinion. The pinion and gear wheel drive have a mechanical efficiency of 90%. A collar bearing 250 mm outside diameter and 100 mm inside diameter takes the axial thrust on the screw. Assuming uniform pressure conditions, determine the pinion shaft's minimum diameter and nut height when the coefficient of friction for the vertical screw and nut is 0.15 and the collar bearing's coefficient of friction is 0.20. The maximum allowable shear stress in the shaft material is 56 Mpa and allowable bearing pressure is 1.4 N/mm2.
A16)
Given: d = 100 mm; p = 20 mm; W = 18 kN = 18 × 103N; No. Of teeth on gear wheel = 80; No. Of teeth on pinion = 20; ηm = 90% = 0.9; D1 = 250 mm or R1 = 125 mm; D2 = 100 mm or R2 = 50 mm; μ = tan φ = 0.15; μ1 = 0.20; τ = 56 MPa = 56 N/mm2; pb = 1.4 N/mm2.
Minimum diameter of pinion shaft
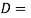 Minimum diameter of pinion shft
Minimum diameter of pinion shft
Since the screw is two start square threaded screw, therefore lead of the screw=2p=2×20=40 mm
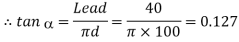
And torque required to overcome friction at the screw and nut,
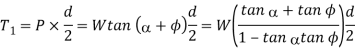
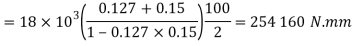
=254.16 N.m
We know that, for uniform pressure conditions, torque required to overcome friction at the collar bearing,
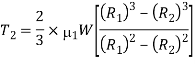
Since the mechanical efficiency of the pinion and gear wheel is 90%., therefore net torque required at the pinion shaft,
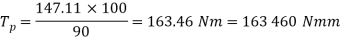
We know that the torque required at the pinion shaft 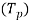
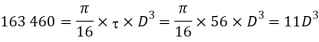
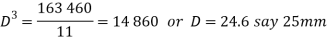
Height of nut
Let h= Height of nut
n=number of threads in contract, and
t= Thickness or width of thread =p/2 =20/2 =10mm
We know that the bearing pressure (
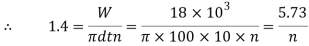
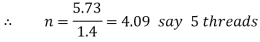
And height of nut, 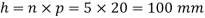
Q17) A power screw having double start square threads of 25 mm nominal diameter and 5 mm pitch is acted upon by an axial load of 10 kN. The outer and inner diameters of screw collar are 50 mm and 20 mm respectively. The coefficient of thread friction and collar friction may be assumed as 0.2 and 0.15 respectively. The screw rotates at 12 r.p.m. Assuming uniform wear condition at the collar and allowable thread bearing pressure of 5.8 N/mm2, find: 1. The torque required to rotate the screw; 2. The stress in the screw; and 3. The number of threads of nut in engagement with screw.
A17)
Given: do = 25 mm; p = 5 mm; W = 10 kN = 10 × 103 N; D1 = 50 mm or R1 = 25 mm; D2 = 20 mm or R2 = 10 mm; μ = tan φ = 0.2; μ1 = 0.15; N = 12 r.p.m.; pb = 5.8 N/mm2
1. Torque required to rotate the screw
We know that means diameter of the screw.
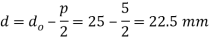
Since the screw is a double start square threaded screw, therefore lead of the screw,
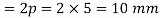
∴ 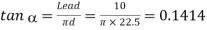
We know that tangential force required at the circumference of the screw,

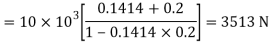
And mean radius of the screw collar,
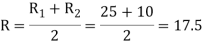
∴ Total torque required to rotate the screw,
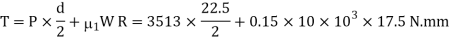
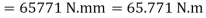
2. Stress in the screw
We know that the inner diameter or core diameter of the screw,
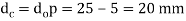
∴Corresponding cross-sectional area of the screw,
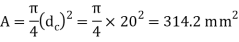
We know that direct stress,
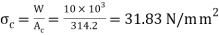
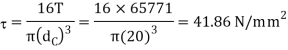
We know that maximum shear stress in the screw
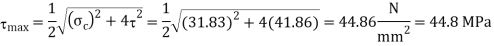
3. Number of threads of nut in engagemetn with screw
Let 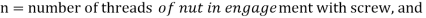
t= Thickness of threads=p/2=5/2=2.5 mm
We know that bearing pressure on the threads(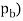
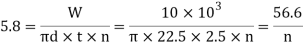
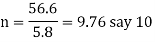
Q18) Draw the square, ACME, Buttress & knuckle threads & Represent terminology of screw threads in diagram.
A18)