Unit - 1

Force Analysis of Mechanism

Q1) What do you mean by Static force Analysis and their necessary condition.

A1) Static force Analysis

The analysis is carried out by determining all the forces and couples acting on all the pairs. In this analysis, we ignore the forces due to acceleration. Only the effects of external forces applied to the mechanism are considered.

Necessary conditions for static equilibrium of a body for a planar system:

A body is said to be in static equilibrium if it remains in its state of rest or motion. The necessary conditions of static equilibrium are as follows:

(i)The vector sum of all the forces on body must be zero, that is ∑F=0.

(ii)The vector sum of all the moment about any arbitrary point must be zero, that is, ∑M=0.

If the body is planar or of 2-Dimensional system, motion then the conditions of static of static equilibrium are as follows:

(i)∑Fx=0, that is, sum of all the horizontal components must be zero.

(ii)∑Fy=0, that is, sum of all the vertical components must be zero.

(iii)∑M=0, that is, sum of all the moment about any arbitrary point must be zero.

Q2) Derive the expression of Correction Torque.

A2)

Consider two masses, one at A and the other at D be placed arbitrarily.

Let l3  = Distance of mass placed at D from G,

l1= New mass moment of inertia of the two masses;

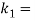New radius of gyration;

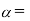Angular acceleration of the body;

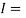Mass moment of inertia of dynamically equivalent system;

Radius of gyration of a dynamically equivalent system. We know that the torque required to accelerate the body

Similarly, the torque required to accelerate the two-mass system placed arbitrarily,

∴ Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body.

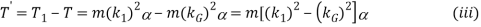
The difference of the torques T' is known as correction Torque. This couple must be applied, when the masses are placed arbitrarily to make the system dynamical equivalent. This, of course, will satisfy the condition (iii).

Q3) State the conditions for static equilibrium of a body, subjected to a system of i) two forces ii) three forces.

A3)

(i)                Equilibrium of two-force member: A member under the action of any two forces will be in equilibrium if the force act along the same line, equal in magnitude but opposite in direction as shown in fig.1.1.

(ii)              Equilibrium of three-force member: A member is under the action of three forces will be in equilibrium if -

1. The resultant is zero.
2. The line of action of the forces intersects at a point known as point of concurrency.
3. A member acted upon by the three forces F1, F2 and F3 as shown in fig.1.2 is an equilibrium as the lines of action of forces intersect at a point O and the resultant is zero.

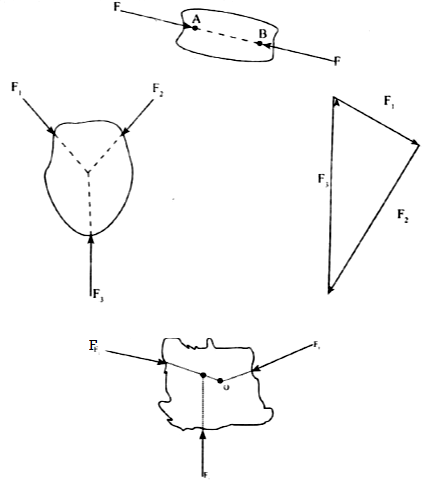
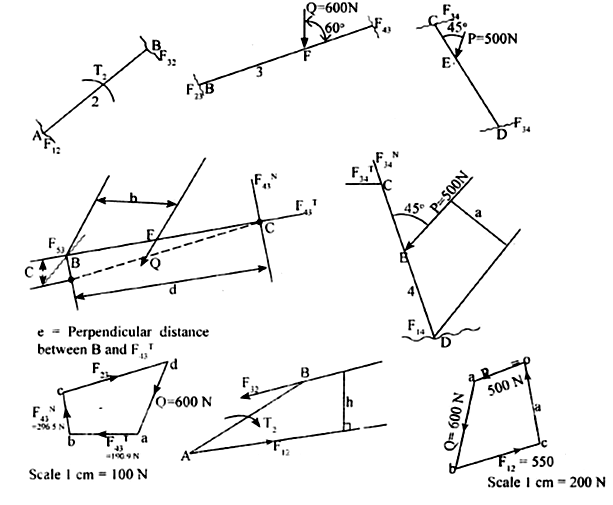
Q4) A four bar mechanism under the action of two external forces is shown in the Fig. Q l(b). Determine the torque to be applied on the Iink AB for static equilibrium. The dimensions of the links are AB = 50 mm, BC = 66 mm, CD = 55 mm, CE = 25 mm, CF = 30 mm, AD=100 mm, angle BAD = 60°, P = 500N and Q = 600N.

A4)

Fig. Q1(b)

Step 1: Draw the figure to scale as shown in fig 1.58

Step 2: to find the forces and couple, draw the free body diagram of each link shown in fig 1.59.

Step 3: Consider the  link 3 and link 4 as shown in Fig. 1.60

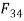is resolved into two components 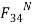and 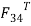which are parallel and perpendicular respectively to the link CD. The magnitude of 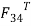os found by taking moments about D.

∴

∴

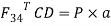
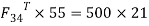
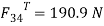
On link 3 the reaction at C are equal and opposite to those at C on link 4. If  we examine link 3, we notice that there are three unknowns. Magnitude and directions of 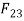and magnitude of 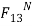. The magnitude of 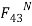of can be found by taking moments about B.

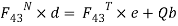
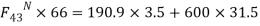
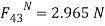
(Assume 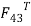direction is toward left downward and 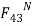direction is upward. Since 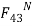is positive (i.e. +269.5 N), the assumed directions are correct.)

Q5) Explain the procedure for static force analysis of four bar mechanism.

A5)

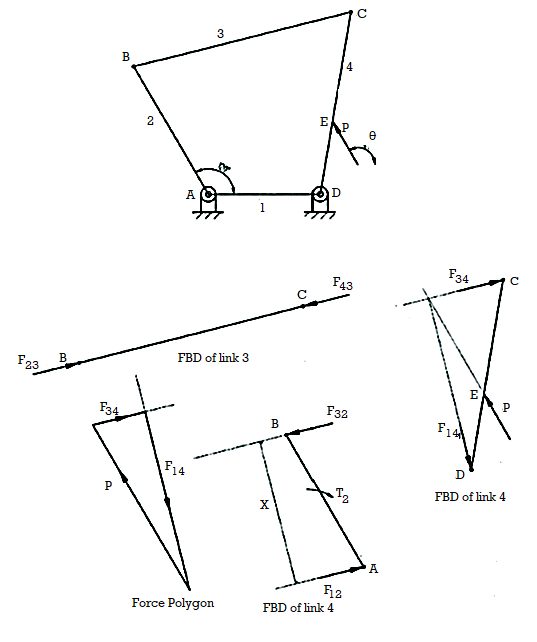
Analysis of Four – Bar Mechanism

Consider a four bar mechanism as shown in Fig 2.1 with a known force F acting on the link 4.

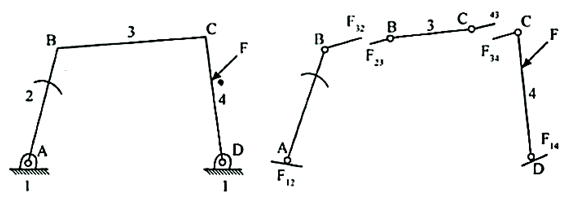
Our aim to find the forces on various links including the Torque 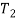on the link 2 to find these forces and the couple. First draw the free body diagram of each ink as shown in Fig.

Link 4: First consider link 4. There are three forces acting on link 4. They are F, 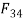and 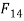. F is known in magnitude and direction. Since link 3 is a two force member (i.e., 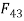and 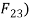, for equilibrium these two forces must be equal and opposite and acts along the axis of BC. But since 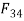and 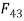are equal and opposite 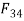must act along the axis BC. For the link 4 to be in equilibrium, 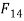must pass through the intersection of F and 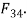Therefore the direction of 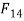is obtained as shown in Fig 2.3.

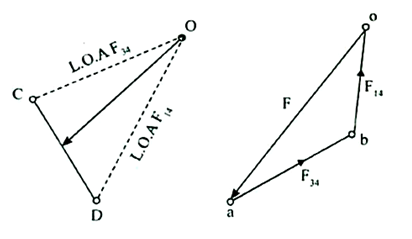
i.e., Form C draw a line parallel to BC (L.O.A.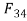) It intersects the extension of F line at O. Join D to O. Now DO is the line action (L/O.A) of .

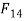Then draw the force polygon for link 4 as shown in Fig 2.4 draw oa parallel to force F and magnitude equal to F. From ‘a’ draw a line parallel ot L.O.A of 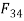and from o draw a line parallel to L.O.A of 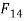. These two lines will intersect at ‘b’, Now 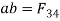and 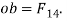If the force polygon is drawn to scale, hten multiply the corresponding values with the scale.

Link 3:

It is two force member i.e., 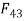and 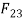, For equilibrium these two forces must be equal, opposite and along the axis of BC. But since 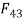and 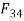are equal and opposite.

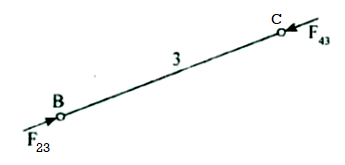
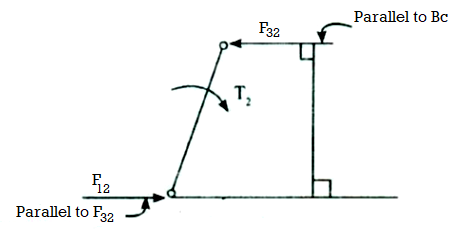
Link 2:

It is two force member 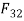and 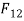and a torque 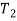. For equilibrium these two forces must be equal and opposite and the torque produced by these two forces must be equal and opposite to the applied torque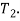

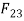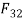But and are equal and opposite, its direction is parallel to BC as shown in Fig 2.6.

∴

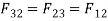
h=perpendicular distance between 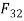and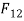

∴ Torque,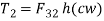

Q6) For the static equilibrium of the mechanism shown in Fig. Ql (b), find the required input torque T2• The dimensions are AB=150mm, BC=AD=500mm, DC=300mm, CE=100mm, and EF=450mm.

A6)

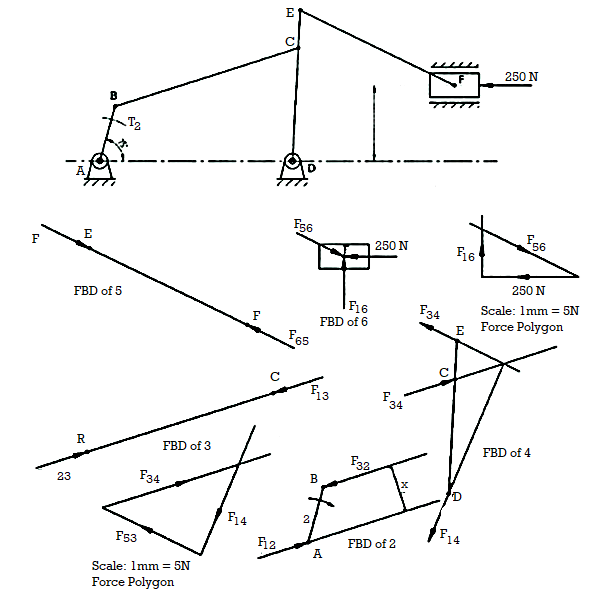
From FBD of link 6 and force polygon

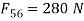
From FBD of link 5

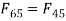
But

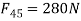
Also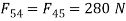

From force polygon of link 4

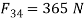
Also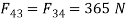

From FBD of link 3

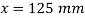
Torque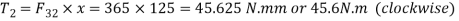

Q7) For a mechanism shown in Fig. Ql (b), find the required input torque, for the static equilibrium. The lengths OA and AB are 250 mrn and 650 mm respectively. F = 500N.

A7)

F32= F23= 477.5N

From BD of link 2

x=144mm

Torque on link 2

T2 = F32X X = 477.5144=68.76 N-m

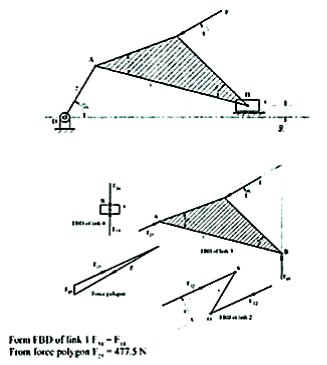
Q8) A four bar mechanism shown in Fig.Ql(b) is acted upon by a force P =100 N at 120° on link CD. The dimensions of various links are AD;'" 40 mm, BC = 60 mm, CD = 50mm, AD = 30 mm, DE = 20 mm, Determine the input torque on link AB for static equilibrium.

A8)

From FBD of link 3 F23=

F43 From force polygon

'F'4 ~ 96.2N

F34= 27.7N F43=

F34= 27.7N

And F23= Fn = 27.7N

From FBD of link 4 x = 38.5 mm

Torque on link 2, T2 = F32X X = 27.738.5 = ·1066.45 N.mm(cw)

Q9) Explain principle of virtual work application to static force analysis.

A9) Another approach to force - analysis is based on the principle of virtual (imaginary) work. This method is based on an energy balance of the system, which requires that the net change in internal energy of a system during small displacement must be equal to the difference between the work input to the system and the work output including the work dine against friction, if any, Therefore if a system which is in equilibrium under the action of difference forces, is given a small displacement from equilibrium, then the net change in the internal energy will be equal will be equal to the work done on the system. In short the principle of virtual work can be stated as "The work done during virtual displacement from the equilibrium is equal to zero.

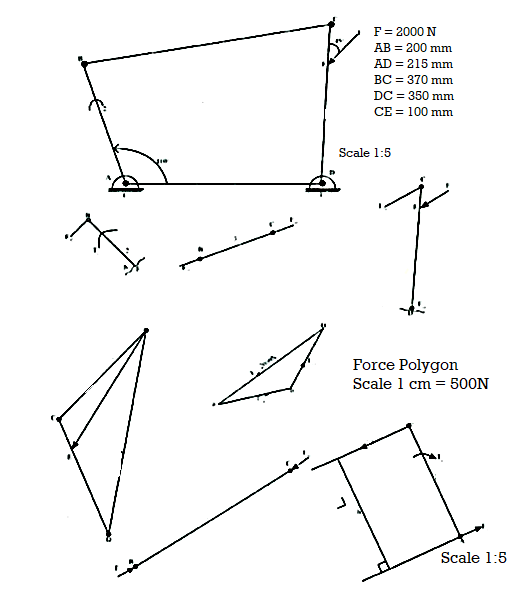
Q10) A four bar mechanism under the action of external force is shown in Fig. Ql (b). Determine the torque T, and various forces on links for the equilibrium of the system.

A10)

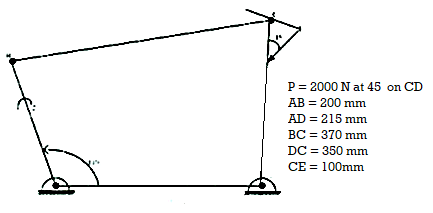
Step: 1

Draw the given figure to scale 1: 5. It is shown in Fig.

Step: 2

To find the forces and couple, draw the free body diagram of each link as shown in Fig: 1.53.

Step: 3

Consider link: 4

It is a three-force member. They are F = 2000 N, Fl4 and Fu. F is known in magnitude and direction, for FJ4 direction known and magnitude is unknown. The direction of Fu is found as shown in Fig: 1.54 [For explanation refer analysis of 4 bar mechanism]

Step: 4

Draw the force polygon for link. 4 as shown in Fig. 1.55 [for explanation refer analysis of 4 bar mechanism] From force polygon-

FJ4 = ab x scale == 2.4 x 500 = 1200 N

Consider link: 3

It is a two-force member i.e., F43 and F23 For equilibrium these two forces are equal and opposite and acts along axis of BC. But since F43and F34arte equal and opposite. F34 = F43= F23 = 1200 N

Step: 6

Consider link: 2

It is a two force member i.e., F32and F,~ and a torque T2 .

F3~and F23 are equal and opposite Also for equilibrium F)2 and FI2 are equal and opposite as shown in Fig Fl.I=F32=FI2= 1200N

Now. Torque, T1 = FJ2 h, where h = 3.96 x5 = 19.8 cm = 198 mm

= 1200 x 198

= 237600 N mm

= 237.6 Nm(cw)