Unit - 1
Introduction to three modes of heat transfer
Q1) Given: A jet aircraft compartment is assumed to be a cylindrical tube of 3-m diameter and 20-m length. It is lined inside with 3 cm of insulating material of k = 0.042 W/mK. It is flying at a height where the average outside temperature is – 30°C. To find: The rate of heating required to maintain the compartment at 20°C for passenger comfort.
A1)
The rate of heat loss from the cylindrical compartment is given by
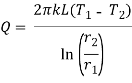
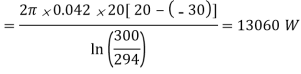
= 13.06 kW Ans.
This is the heat which must be supplied to the compartment to make up for the heat loss through the walls.
Q2) Given: A furnace wall has the inside surface temperature of 1100°C, while the ambient air temperature is 25°C. The wall consists of 125 mm thick refractory bricks (k = 1.6 W/mK), 125 mm thick firebricks (k = 0.3 W/mK) and 12 mm thick plaster (k = 0.14 W/mK). There is an air gap which offers a thermal resistance of 0.16 K/W. The heat transfer coefficient on the outside wall to the air is 17 W/m2K. To find: (a) The rate of heat loss per unit area of wall surface, (b) the interface temperatures throughout the wall, and (c) the temperature of the outside surface of the wall.
A2)
There are a number of thermal resistances in series to heat flow from the inside fumace wall to the ambient air. The rate of heat flow Q is given by,
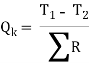
Where T1 = 1100oC, T2 = 25oC and
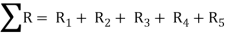
And R1 = Resistance of the refractory brick = 
R2 = Resistance of the insulating firebricks = 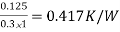
R3 = Resistance of plaster = 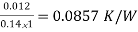
R4 = Resistance of air film on outside surface = 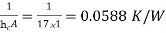
R5 = Resistance of air gap = 0.16 K/W
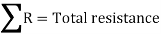
= 0.0781 + 0.417 + 0.0857 + 0.0588 + 0.16
= 0.7996 ≅ 0.8 K/W
Rate of heat loss per unit area

The interface temperatures are T3, T4 and T5 and the outside surface temperature is at T6
Qk = 1344 = (1100 – T3)/0.0781
T3 = 995oC Ans. (b)
Qk = 1344 = (T3 – T4)/R5 = (995 – T4)/0.16
T4 = 780oC Ans. (b)
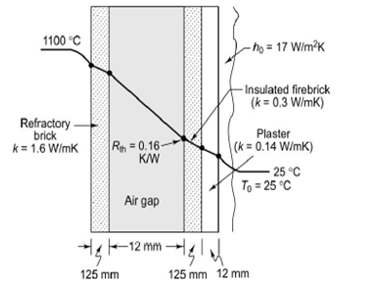
Qk = 1344 = (T4 – T5)/R2 = (780 – T5)/0.417
T5 = 220o C Ans. (b)
Qk = 1344 = (T5 – T6)/R3 = (220 – T6)/0.0857
T6 = 104.1oC Ans. (c)
However, the outside furnace wall surface temperature should be below 60oC to avoid any injury to the person touching the wall.
Q3) Given: A plastic pipe (k = 0.5 W/mK) of inner diameter 3 cm and outer diameter 4 cm carries a fluid of average temperature 100°C and h = 300 W/m2K. The rate of heat transfer per unit length is 500 W/m.
To find: (i) The outside surface temperature of pipe, (ii) the overall heat transfer coefficient based on outside area.
A3)
Solution The rate of heat transfer per unit length of the plastic pipe is given by
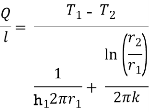
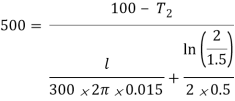
T2 = outside surface temperature of pipe = 36.5oC Ans.
Now, 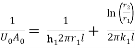
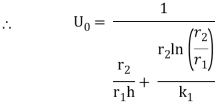

As a check, Q = U0A0(T1 – T2) = 62.69 2π 0.02 (100 – 36.5) = 500 W/m
Q4) Given: Steam at 350°C flowing in a pipe (k = 80 W/mK) 5 cm inner diameter 5.6 cm outer diameter is covered with 3 cm thick insulation (k = 0.05 W/mK). Heat is lost to the surroundings at 5°C by natural convection and radiation with combined h = 20 W/m2K and hi = 60 W/m2K.
To find: (i) The rate of heat loss from the pipe per unit length, (ii) the temperature drops across the pipe and the insulation.
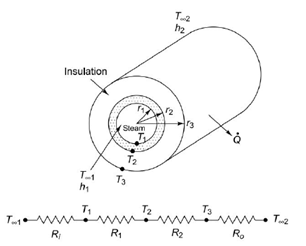
A4)
For steady one-dimensional heat transfer through the pipe, the thermal resistances in series are given in Fig. Ex. 1.16.
A1 = 2πr1L = 2π 0.025 1 = 0.157 m2
A2 = 2πr2L = 2π 0.058 1 = 0.364 m2
Ri = 1/(hiAi) = 1/(60 0.157) = 0.106 K/W
R1 = ln(r2/r1)/2πk1L = ln(2.8/2.5)/2π801 = 0.00023 K/W
R2 = ln(r3/r2)/2πk2L = ln(5.8/2.8)/2π 0.05 1 = 2.318 K/W
R0 = 1/h0A3 = 1/(20 0.364) = 0.137 K/W
Rtotal = Ri + R1 + R2 + R0
= 0.106 + 0.00023 + 2.318 + 0.137
= 2.56123 K/W
(i) Rate of heat transfer Q = 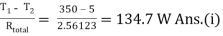
(ii) Tpipe = QR1 = 134.7 0.00023 = 0.03oC
Tinsulation = QR2 = 134.7 2.318 = 312.2oC Ans. (ii)
Q5)Given: A pipe 2 cm in dia. At 40°C is placed in (i) an air flow at 50°C, with h = 20 W/m2K and in (ii) water at 30°C with h = 70 W/m2K.
To find: The heat transfer rate per unit length of the pipe.
A5)
The definition of the mean heat transfer coefficient gives
Q = hA (Tw - T)
Here Tw = 40oC, and since 1 m length of pipe is being considered
A = πDL = π 0.02 m2
Q = hπ 0.02 (40 - T)
For case (i),
Q = 70 π 0.02 (40 – 30)
= 43.98 W
This result is positive which indicates the heat transfer to be occurring from the cylinder to the water. Ans.
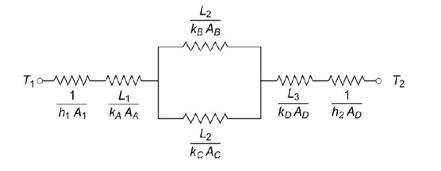
Q6) Given: The composite wall having unit length normal to the plane of paper and the equivalent thermal circuit are shown in Figure
HA = HD = 3 m, HB = HC = 1.5 m
L1 = L3 = 0.05 m, L2 = 0.1 m
KA = kD = 50 W/mK, kB = 10 W/mK, kC = 1 W/mK
T1 = 200ºC, h1= 50 W/m2 K, T2 = 25ºC, h2 = 10 W/m2K.
To find: The rate of heat transfer through the wall.

A6)
The total thermal resistance
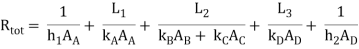

= 0.0467 mK/W
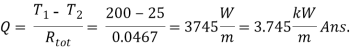
Q7) A stainless steel fin (k = 20 W/m K) having a diameter of 20 mm and a length of 0.1 m is attached to a wall at 300°C. The ambient temperature is 50°C and the heat transfer coefficient is 10 W/m2 K. The fin tip is insulated.
Determine (a) the rate of heat dissipation from the fi n, (b) the temperature at the fi n tip, (c) the rate of heat transfer from the wall area covered by the fi n if the fi n was not used and (d) the heat transfer rate from the same fin geometry if the stainless steel fin is replaced by a fictitious fin with infinite thermal conductivity.
A7)
(a) The heat transfer rate from the fin
Q0 = (hPkA)1/2 θ0 tanh ml
Where m = (hP/kA)1/2 = 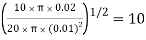 m-1
m-1
ml = 10 0.1 = 1
Q0 = [ 10 π 0.02 20 π (0.01)2]1/2 (300 – 50 ) tanh (1)
= 0.06283 250 tanh (1) = 11.96 W Ans. (a)
(b) The fan tip temperature is given by
θ1 = 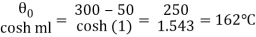
T1 = 162 + 50 = 212oC Ans. (b)
(c) Q = hA(T0 - T) = 10 π (0.01)2 (300 – 50)
= 0.785 W Ans. (c)
The presence of fin increases heat dissipation 11.96/0.785 or 15.24 times
(d) Qideal = h As(T0 - T)
= 10 π (0.02)(0.1)(300 – 50)
= 15.71 W
The stainless steel fin dissipates
(15.71 – 11.96)/15.71 = 0.24
Or 24 % less heat than the ideal fin of infinite thermal conductivity
Q8) A copper fin (k = 396 W/mK) 0.25 cm in diameter protrudes from a wall at 95°C into ambient air at 25°C. The heat transfer coefficient by free convection is equal to 10 W/m2K. Calculate the heat loss if (a) the fin is infinitely long, (b) the fin is 2.5 cm long and the coefficient at the end is the same as around the circumference.
A8)
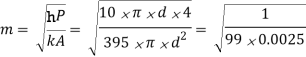
= 2.01 m-1
(a) For infinitely long fin,
Q0 = mkAθ0
= 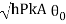
= 
= 0.865 W Ans.
(b) Q0 = hPkA (T0 - T) 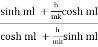
Ml = 2.01 0.025 = 0.05025
h/ml = 10/(2.01 396) = 0.01256
Substituting: Q0 = 0.865 
Q0 = 0.140 W Ans.
Q9) The body of an electric motor is 360 mm in diameter and 240 mm long. It dissipates 360 W of heat and its surface temperature should not exceed 55°C. Longitudinal fi ns of 15 mm thickness and 40 mm height are proposed. The heat transfer coefficient is 40 W/m2 K when the ambient air is 30°C. Determine the number of fins required, if k of the fin material is 40 W/mK.
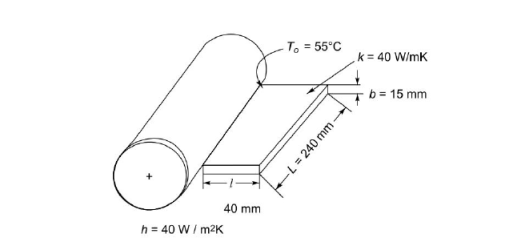
A9)
The rate of heat transfer in one fin
Q0 = hPkA, θ0 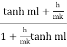
Where m = hP/kA = 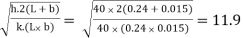 m-1
m-1
ml = 11.5 0.04 = 0.476
Q0 = 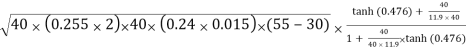
= 1.714 25 
Number of fins required = 360/21.77 = 16.356 or 17 fins Ans.
Q10) A square plate 1 kW electric heater (150 mmx 150 mm) is inserted between two slabs. Slab A is 20 mm thick (k = 50 W/mK) and slab B is 10 mm thick (k = 0.2 W/mK). The outside heat transfer coefficients on side A and side B are 200 W/m2 K and 50 W/m2 K respectively. The temperature of surrounding air is 25°C.
Estimate (a) the maximum temperature in the system and (b) the outside surface temperatures of the two slabs. Draw the equivalent electrical circuit.
LA = 0.02 m, LB = 0.01 m,
KA= 50 W/mK, kB = 0.2 W/mK, h1 = 200 W/m2K,
H1 = 50 W/m2 K,  = 25°C
= 25°C
A10)
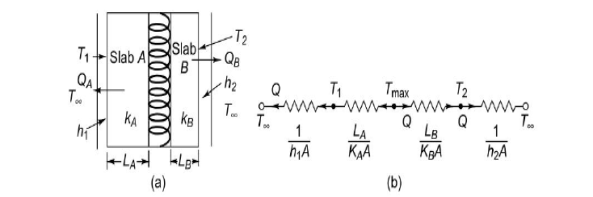
Equivalent electrical circuit is shown in (b).
A = 0.15 0.15 = 0.0225 m2
Q = 1kW = 1000 W
Q = QA + QB = 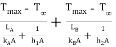

1000 = 0.0225 (Tmax – 25) 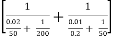
= 0.0225 (Tmax – 25) 199.47
Tmax = 25 + 1000/(0.0225 199.47) = 247.81oC Ans.
QA = 
50(247.81 – T1)/0.02=200(T1- 25)
T1 = 231.3oC Ans.
Similarly, QB = 0.2A(247.81 – T2)/0.01 = 50 A ()T2 – 25)
20(247.81 – T2) = 50 (T2 – 25)
Or, 247.81 – T2 = 2.5 T 2 – 62.5
T2 = 88.66oC Ans.