Unit - 3

Interaction of Radiation with Materials

Q1) A domestic hot water tank (0.5 m diameter and 1 m high) is installed in a large space. The ambient temperature is 25°C. If the tank surface is oxidised copper with an emissivity of 0.8, find the heat loss from the tank surface at temperature 80°C by radiation. What would be the reduction in heat loss if a coating of aluminiumpaint having an emissivity of 0.3 is given to the tank? What would be the increase in heat loss if a white paint having an emissivity of 0.97 is given to the tank?

A1)

Since the tank is small compared to the surrounding space, F12 = 1 = 0.8

1 = πdl + 2 π/4 d2 = π  0.5  1 + 2  π/4  (0.5)2

= 5π/8 m2

Rate of heat loss from the tank by radiation

Q12 = σA1F12(T14 – T24)

= 5.67  10-8  5π/8  0.8 [ (353)4 – (298)4]

= 690 W

If the tank is coated with aluminum paint ( = 0.3), the reduction in heat loss

= (0.8 – 0.3)/0.8  690 = 430 W

       Q12 = 260 W

If the tank is coated with white paint ( = 0.97), the rate of radiant heat loss

Q12 = 690/0.8  0.97 = 835.62 W Ans.

Q2) A black body emits radiation at 2000 K. Calculate (i) the monochromatic emissive power at 1 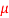m wavelength, (ii) wavelength at which the emission is maximum, and (iii) the maximum emissive power.

A2)

(i) From Planck’s law,

Ebλ = c1λ-5/(ec2/πT – 1)

= (3.74  10-16(1  10-6)-5/(e1.438  10^-2/(10^-6  2000) – 1)

= 2.79  1011 W/m3 Ans.

(ii) From Wien’s displacement law,

λmax T = 2.898  10-3 mK

λmax = (2.898  10-3)/2000 = 1.449  10-6 m ANs.

(iii) (Ebλ)max = c1λmax-5/(ec2/λmax T -1)

= (3.74  10-16 (1.449  10-6)-5)/(e0.01433/(1.449  10 ^ -6  2000)-1)

= 4.1  1011 W/m3 Ans.

Q3) The filament of a 75 W light bulb may be considered a black body radiating into a black enclosure at 70°C. The fi lament diameter is 0.10 mm and length is 50 mm. Considering the radiation, deter mine the fi lament temperature.

A3)

Given: Q = 75 W, T2 = 70 + 273 = 343 K, d = 0.1 mm, l = 50 mm,T1 = filament temperature, 1 = 1

Q = σ  A(T14 – T24)

75 = 5.67  10-8  1  π  0.1  10-3  50  10-3  (T14 – 3434)

= 8.906  10-13(T14 – 3434)

T1 = 3029 K = 2756oC Ans.

Q4) Assuming the sun as a black body, it emits maximum radiation at 0.5 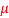m wavelength. Calculate (i) the surface temperature of the sun, (ii) its emissive power, (iii) the energy received by the surface of the earth and (iv) the energy received by a 2 m 2 m solar collector whose normal is inclined at 60° to the sun. Take the diameter of the sun as 1.4 109 m, diameter of the earth as 13 106 m and the distance of the earth from the sun as 15 1010m.

A4)

From Wien’s displacement law,

λmax T = 2898  106mK

 Surface temperature of the sun

T = (2898  106)/(0.5  10-6) = 5796 K   Ans. (i)

Emissive power of the sun, a black body, is obtained from Stefan- Boltzmann law:

Eb = σ T4 = 5.67  10-8 (5796)4 = 63865 kW/m2   Ans (ii)

Radiation reaching the earth would be

= Emissive power of the sun  (Radius of the sun/ Distance from the earth)2

= 63865  (0.7  109/15  1010)2 = 1.39 kW/m2 Ans. (iii)

Surface area of the solar collector in the direction normal to solar radiation

= A cos θ = 4 cos 60o = 2 m2

 Energy received by the solar collector

= 1.39  2 = 2.78 kW    Ans (iv)

Q5) A sphere of radius 5cm is concentric with another sphere. Find radius of outer sphere so that shape so that shape factor of outer sphere with respect inner sphere is 0.6.

A1=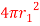 and A2= 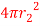 F21=0.6

A5)

Since inside sphere is completely enclosed in outer sphere F11=0

By enclosure theorem

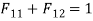
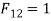
By reciprocating theorem

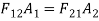
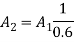
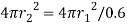
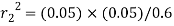
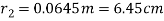
Q6) A double-walled thermos flask may be assumed to be equivalent to two infinite parallel plates. The emissivities of wall are 0.3 and 0.7 respectively. Space between them is evacuated. Find the heat transfer rate by radiation through the flask if inside surface temperature is 90oC and outside surface temperature at 30oC under steady state.

A6)

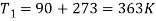
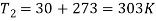
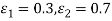
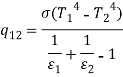
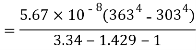
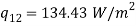
Q7) A spherical ball 6 cm in diameter and 310 K is placed inside a large spherical furnace at 600 K. Estimate the diameter of the spherical furnace such that 20% of the energy emitted by the furnace reaches the spherical ball. Assume the surfaces as black. What is the net exchange of energy between the two surfaces?

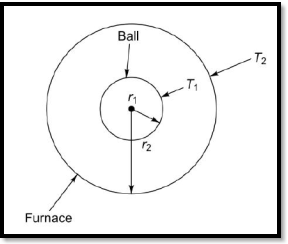
Fig.1

A7)

  T1 = 310 K, T2 = 600 K, r1 = 3 cm, r2 = ?

F11 + F12 = 1.0

Since F11 = 0, F2= 1.0

A1F12= A2 F1, F21 = A1/A2

Energy emitted by the inside surface of the sphere = A2E and the fraction reaching the spherical ball is 0.2 A2E2.

 F21 = 0.2 = A1/A2 = 4πr12/4πr22

r2 = r/0.2 = 3 cm/0.447 = 6.71 cm

 Diameter of the furnace = 13.42 cm Ans.

Net exchange of energy between the two surfaces

Q1-2 = σ A1 F12 (T14 – T24)

= 5.67  4π (0.3)2  1  (3.14 – 64)

= - 77. 195 W Ans.

Q8) A small sphere (outside radius = 60 mm) with a surface temperature of 300°C is located at the geometric centre of a large sphere (inside diameter = 360 mm) with an inner surface temperature of 15°C. Calculate how much of heat emitted from the large sphere inner surface is incident upon the outer surface of the small sphere, assuming that both surfaces approach black body behavior. What is the net exchange of heat between the two spheres?

A8)

Radius of small sphere, r = 30 mm = 0.03 m, Radius of large sphere r2 = 180 mm = 0.18 m.

Here F12 = 1|

By reciprocity theorem,

A1F12 = A2F21

F21 = A1/A2 = r12/r22 = (0.03/0.18)2 = 0.0278 Ans.

Thus, 2.78% of the emission from the inner surface of the large sphere is incident upon the small sphere and absorbed by it.

 Also, F21 + F22 = 1

     F22 = 1 – F21 = 1 – 0.0278 = 0.9722

Thus, 97.22% of emission from the large sphere is absorbed by the inner surface of the sphere itself.

Radiant heat exchange between the two spheres

Q2 = σA1F12(T14 – T24)

= 5.67  4π(0.03)2  1  [ (573/100)4 – (288/100)4]

= 0.0113  5.67  1009.2 = 64.66 W Ans.

Q9) Explain and derive Stefan–Boltzmann Law

A9)

It states that total emissive power of black body is directly proportional to fourth power of absolute temperature.

Planck’s law also permits to derive Stefan–Boltzmann law, which establishes thedependence of total hemispherical radiation on temperature.

The total emissive power of a black body is given by

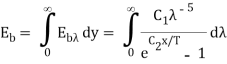
Substituting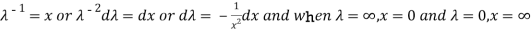

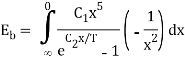
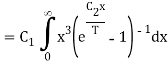
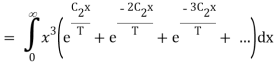
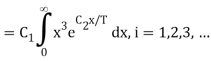
Since

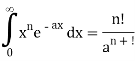
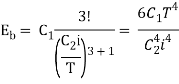
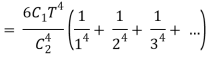
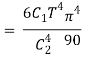
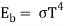
Where 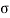is the Stefan-Boltzmann constant.

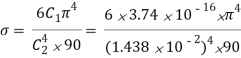
=5.67  X 10-8 W/m2 K4

Q10) Classify the bodies based on their radiative characteristics.

A10)

• Black body-The body which absorbs entire radiations and emits maximum radiations is called a black body.

It implies that ,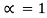

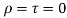
No perfect black body exist.

• Opaque body- The bodies or surfaces which have negligible transmissivity of energy are called opaque bodies e.g. Solid and liquid surface.                                        By opaque surface the radiant energy received is either absorbed or reflected i.e. 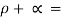1 and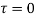
• White body-The surface which reflects total radian energy are called white bodies.

For such bodies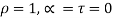

• Grey body-The body which has its absorptivity equal to its emissivity is called a grey body provided the temperature of the surface of incident radiation and the body are same.