Unit - 4
Types of heat exchangers
Q1) Two fluids A and B exchange heat in a counter flow heat exchanger. Fluid A enters at 420°C and has a mass flow rate of 1 kg/s. Fluid B enters at 20°C and has a mass flow rate of 1 kg/s. The effectiveness of heat exchanger is 75%. Determine (i) the heat transfer rate, (ii) the exit temperature of fluid B. Specific heat of fluid A is 1 kJ/kgK and that of fluid B is 4 kJ/kgK.
A1)
Cmin = CA =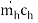 
= 1 1 = 1 kW/K
Cmax = CB =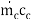 
= 1 4 = 4 kW/K
(DT)1 = Th1 – Th2
= (DT)1/(Th1 – Tc1) = (Th1 – Th2)/(Th1 – Tc1) = (420 – Th2)/(420 – 20) = 0.75
Th2 = 420- 0.75 400 = 120oC Ans.
Q =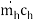 
(Th1 – Th2) = 1 1 (420 – 120)
= 300 kW Ans.(i)
Q =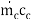 
(Tc2 – Tc1) = 1 4 (Tc2 – 20) = 300
Tc2 = 95oC Ans. (ii)
Q2) A chemical having specific heat of 3.3 kJ/kgK flowing at the rate of 20,000 kg/h enters a parallel flow heat exchanger at 120°C. The flow rate of cooling water is 50,000 kg/h with an inlet temperature of 20°C. The heat transfer area is 10 m2 and the overall heat transfer coefficient is 1050 W/m2 K. Find (i) the effectiveness of the heat exchanger, (ii) the outlet temperatures of water and chemical. Take for water Cp= 4.186 kJ/kgK.
A2)
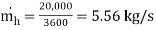, ch= 3.3 kJ/kgK
Ch = 5.56 3.3 = 18.35 kW/K
, cc = 4.186 kJ/kgK
Cc = 13.89 4.186 = 58.14 kW/K
Ch < Cc
Cmin = 18.35 kW/K
NTU = UA/Cmin = (1050 10)/18350 = 0.572
R = Cmin/Cmax = 18.35/58.14 = 0.3156
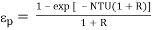
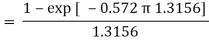
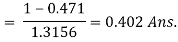
= (DT)1/(Th1 – Tc1) = (Th1 – Th2)/(Th1 – Tc1) = 0.402 = (120 – Th2)/(120 – 20)
Th2= 79.8oC Ans.
(Th1 – Th2 ) = 
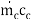(Tc2 – Tc1)
Tc2 – Tc1 = 0.3156 40.2 = 12.69
T2 = 32.69oC Ans.
Q3) A flow of 0.1 kg/s of exhaust gases at 700 K from a gas turbine is used to preheat the incoming air, which is at the ambient temperature of 300 K. It is desired to cool the exhaust to 400 K, and it is estimated that an overall heat transfer coefficient of 30 W/m2K can be achieved in an appropriate exchanger. Determine the area required for a counter flow heat exchanger. Take the specific heat of exhaust gases the same as for air, which is 1000 J/kgK.
A3)
It is also a balanced heat exchanger
Where Ch= Cc = C. The effectiveness is
= (Th1 – Th2)/(Th1 – Tc1) = (700 – 400)/(700 – 300) =0.75
Again, =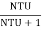 
NTU = /(1-) = 0.75/(1 – 0.75) = 3.0
NTU = UA/C = 3
A = (3 0.1 1000)/30 = 10m2 Ans.
Q4) A 4 kg/s product stream from a distillation column is to be cooled by a 3 kg/s water stream in a counter flow heat exchanger. The hot and cold stream inlet temperatures are 400K and 300 K respectively, and the area of the exchanger is 30 m2. If the overall heat transfer coefficient is estimated to be 820 W/m2K, determine the product stream outlet temperature, if its specific heat is 2500 J/kgK and the coolant outlet temperature.
A4)
The effectiveness of counterflow heat exchanger is given by
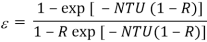
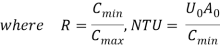
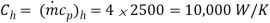
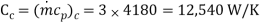
Cmin = 10,000 W/L
R = 10,000/12,540 = 0.797
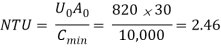
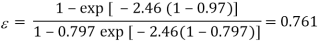
Also,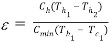 
Or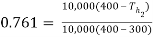 
Th2 = 323.9 K Ans.
By energy balance,
Ch (Th1 – Th2) = Cc (Tc2 – Tc1)
10,000(400 – 323.9) = 12,540(Tc2 – 300)
Tc2 = 360.7 K Ans.
Q5) In a solar-assisted air-conditioning system, 0.5 kg/s of ambient air at 270 K is to be preheated by the same amount of air leaving the system at 295 K. If a counter flow heat exchanger has an area of 30 m2, and the overall heat transfer coefficient is estimated to be 25 W/m2 K, determine the outlet temperature of the preheated air. Take cp for air as 1000 J/kgK.
A5)
It is a balance heat exchanger where Ch = Cc
NTU = UA/C = (25 30)/(0.5 1000) = 1.5
For a balance counterflow heat exchange,
= (Tc2 – Tc1)/(Th1 – Tc1)
0.6 = (Tc2 – 270)/(295 – 270)
Tc2 = 285 K Ans.
Q6) Water (Cp= 4.187 kJ/kg K) is heated at the rate of 1.4 kg/s from 40°C to 70°C by an oil (Cp= 1.9 kJ/kg K) entering at 110°C and leaving at 60°C in a counter flow heat exchanger. If Uo= 350 W/m2K, calculate the surface area required. Using the same entering fluid temperatures and the same oil flow rate, calculate the exit temperatures of oil and water and the rate of heat transfer, when the water flow rate is halved.
A6)
Th1 = 110oC , Th2 = 60oC , Tc1 = 40oC, Tc2 = 70oC
Ti = 110 – 70 = 40oC
Te = 60 – 40 = 20oC
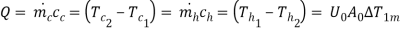
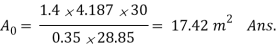
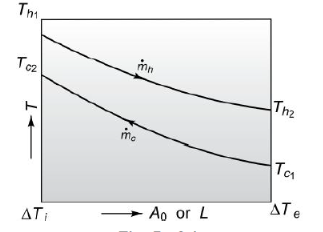
Fig. 1
1.4 4.187 30 = 
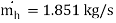
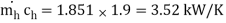
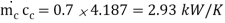
(with water flow halved)
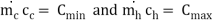
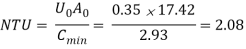
Exp [ - NTU (1 – R)] = exp [ - 2.08 ( 1 – 0.832)]
= e-0.34944 = 0.705
The effectiveness of the heat exchanger is
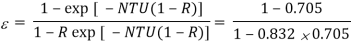
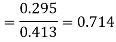
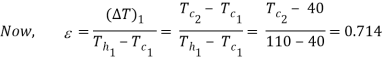
Tc2 = exit water temperature
= 90oC Ans.
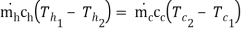
1.851 1.9 (110 -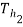 
) = 0.7 4.187 (90 – 40)
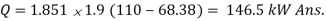
Q7) In an open heart surgery under hypothermic conditions, the patient’s blood is cooled before the surgery and rewarmed after wards. It is proposed that a concentric tube counter flow heat exchanger of length 0.5 m is to be used for this purpose, with a thin-walled inner tube having a diameter of 55 mm. If water at 60oC and 0.1 kg/s is used to heat blood entering the exchanger at 18oC and 0.05 kg/s, what is the temperature of the blood leaving the exchanger and the heat flow rate. Take U0 = 500 W/m2 K, Cpof blood = 3.5 kJ/kg K and Cpof water = 4.183 kJ/kg K.
A7)
Cc =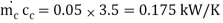 
Ch = 
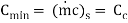
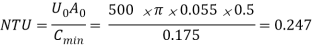
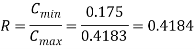
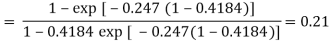
Now, 
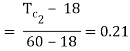
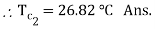
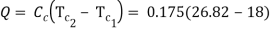
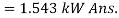
Q8) A counter flow heat exchanger is employed to cool 0.55 kg/s (Cp= 2.45 kJ/kg°C) of oil from 115°C to 40°C by the use of water. The inlet and outlet temperatures of cooling water are 15°C and 75°C, respectively. The overall heat transfer coefficient is expected to be 1450 W/m2K. Using the NTU method, calculate the following: (a) The mass flow rate of water, (b) the effectiveness of the heat exchanger and (c) the surface area required.
A8)
Q =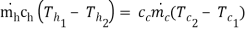 
= 0.55 2.45 (115 – 40) =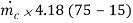 
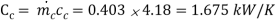
Since Cc > Ch, (Th1 – Th2 ) > (Tc2 – Tc1)
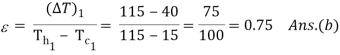
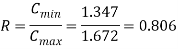
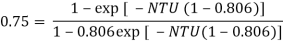
By rearrangement,
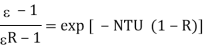
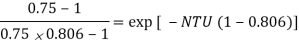
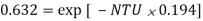
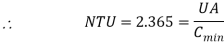
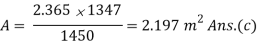
Q9) A counter flow heat exchanger is to heat air entering at 400°C with a flow rate of 6 kg/s by the exhaust gas entering at 800°C with a flow rate of 4 kg/s. The overall heat transfer coefficient is 100 W/m2K and the outlet temperature of air is 551.5°C. Specific heat of air, Cp, for both air and exhaust gas can be taken as 1100 J/kgK. Calculate (i) the heat transfer area needed and (ii) the number of transfer units.
Fig.2
A9)
Ch =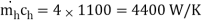 
Cc =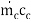 
= 6 1100 = 6600 W/K
Ch < Cc, Cmin =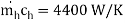 
Q =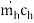 
(Th1 – Th2) = 
(Tc2 – Tc1)
4400(800 – Th2) = 6600 (551.5 – 400)
Th2 = 572.75oC
Q = 999900 W = 999.9 kW
T1.m. = 
= 76.0/0.365 = 208.19oC
Q = U0A0T1.m.
999900 = 100 A0 208.19
A0 = 48.03 m2 Ans. (i)
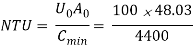
= 1.092 Ans. (ii)
Q10) Explain selection criteria for heat exchanger.
A10)
An engineer going through the catalogs of heat exchanger manufacturers is often overwhelmed by the type and number of readily available off-the-shelf heat exchangers. The proper selection depends on several factors.
- Heat Transfer Rate:
This is the most important quantity. A heat exchanger should be capable of transferring heat at the specified rate in order to achieve the desired temperature change of the fluid at the specified mass flow rate.
- Cost:
Budgetary limitation often restricts the selection of the heat exchanger. An off-the-shelf heat exchanger has a definite cost advantage over those made to order. However, in many cases, the standard available heat exchanger is not satisfactory. It is then needed to undertake the expensive and time-consuming task of designing and manufacturing a heat exchanger from scratch to suit the needs. The operation and maintenance costs of the heat exchanger are also required to consider for assessing the overall cost.
- Pumping power:
In a heat exchanger, both fluids are usually forced to flow by pumps or fans that consume electrical power. The annual cost of electricity associated with the operation of the pumps and fans can be determined from Operating cost = [Pumping power, kW x Hours of operation, h x Price of electricity, Rs. / kWh] where the pumping power is the total electricity consumed by the motors of the pumps and fans.
- Size and weight:
Normally, the smaller and lighter the heat exchanger, the better it is. This is particularly important in automotive and aerospace industries. Also a larger heat exchanger, not only carries a higher price tag, but also requires more space.
- Type:
The type of heat exchanger to be selected depends primarily on the type of fluids involved, the size and weight limitations, and the presence of phase-change processes. A heat exchanger is suitable to cool a liquid by a gas. On the other hand, a plate or shell-and-tube heat exchanger is very suitable for cooling a liquid by another liquid.
