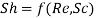Unit - 6

Mass Transfer

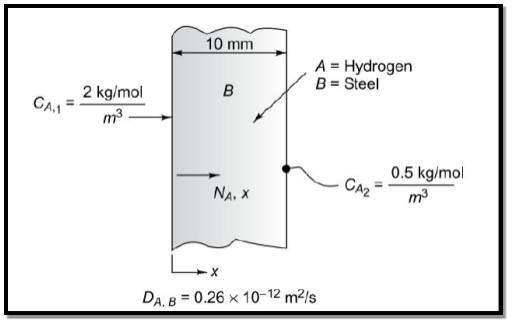
Q1) Gaseous hydrogen is stored at elevated pressure in a rectangular steel container of 10 mm wall thickness. The molar concentration of hydrogen in steel at the outer surface is 2 kgmol/m3, while the concentration of hydrogen in steel at the outer surface is 0.5 kg mol/m3. The binary diffusion coefficient for hydrogen in steel is 0.26 x10–12 m2/s. What is the mass flux of hydrogen through the steel?

A1)

Assuming (a) steady-state one-dimensional diffusion of hydrogen, (b) the molar concentration of hydrogen much less than that of steel CA<<CB, so that C = CA+ CB is uniform and (c) no chemical reaction

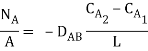
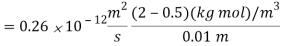
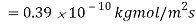
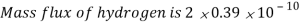
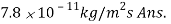
Q2) Hydrogen gas is maintained at 5 bar and 1 bar on opposite sides of a plastic membrane, which is 0.3 mm thick. The temperature is 25°C, and the binary diffusion coefficient of hydrogen in the plastic is 8.7 x 10–8 m2/s. The solubility of hydrogen in the membrane is 1.5 x10–3 kg mol/m3bar. What is the mass flux of hydrogen by diffusion through the membrane?

A2) The surface molar concentrations of hydrogen

CA, 1 = 1.5  10-3  5 = 7.5  10-3 kg mol/m3

CA, 2 = 1.5  10-3  1 = 1.5  10-3 kg mol/m3

NA/A = DAB/L  (CA, 1 – CA, 2)

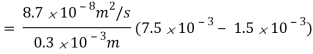
= 17.4  10-7 kg mol/m2s

= 34.8  10-7 kg/m2s        Ans.

Q3) Two large vessels contain uniform mixture of air (component A) and sulphur dioxide (component B) at 1 atm and 273 K, but at different concentrations. Vessel 1 contains 80% air and 20% SO2by volume or mole percentage whereas vessel 2 contains 30% air and 70% SO2 by mole percentage. The vessels are connected by assuming that a steady-state transfer takes place. The mass diffusivity for the air – SO2mixture at 1 atm and 273 K is 0.122 x 10–4 m2/s.

A3)

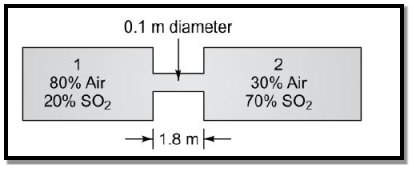
Air diffuses from vessel 1 to 2 and SO2 from vessel2 to 1 due to concentration gradients. Since thevessels are large, the partial pressure of air (A) in both vesselsmay be considered to remain constant, so that steady-statemass transfer takes place. The mass transfer process can be characterized as an equimolar counter diffusion and the massflux of air through the connecting duct can be determined by

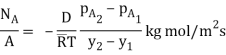
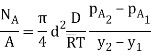
d = 0.1 m, D = 0.122 x10–4 m2/s, T = 273 K, pA1= 0.8 x1 atm = 0.8 atm, pA2= 0.3 x1 atm = 0.3 atm,R = 0.082 m3atm/kg mol-K and y2 – y1 = L = 1.8 m.

NA = π/4   (0.1)2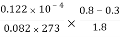

= 0.119  10-6 kg mol/s   Ans.

Q4) Determine the mass diffusivity for CO2 in air at 1 atm, 298 K. Given that atomic volume of CO2 and air is 34.0 and 29.9 respectively.

A4)

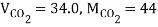
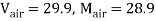
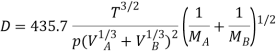
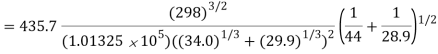
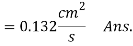
Q5) A deep narrow cylindrical vessel which is open at the top contains some water at the bottom. The air within the vessel is considered motionless, but there is sufficient air current at the top surface of the vessel so that any water vapour arriving at the top surface is immediately removed to ensure zero water vapourconcentration. The entire system is at 1 atm, 298 K. The diffusivity of air-water vapour is D = 0.26 x10–4 m2/s and the saturated vapour pressure of water at the surface is 0.032 atm. Determine the rate of vaporation of water into the air per unit area if the distance between the water surface and the top of the vessel is 1.524 m.

A5) For steady-state unidirectional diffusion of water vapour (component A) through the stationary air (component B) of thick ness 1.524 m.

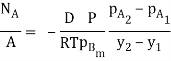
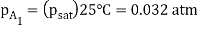
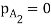
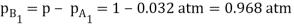
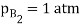
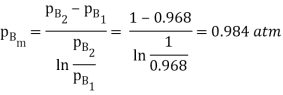
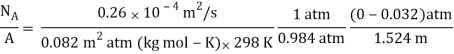
= 6.868  10-7 kg mol/m2s,

= 0.1236  10-4 kg/m2s   Ans.

Q6) In a Stefan tube experiment with carbon tetrachloride and oxygen, the following data are noted:

Diameter of the tube = 10 mm

Length of tube above liquid surface = 150 mm

Temperature maintained = 0°C

Pressure maintained = 760 mm Hg

Vapour pressure of CCl4 at 0°C = 33 mm Hg

Evaporation of CCl4 = 0.03 g

Time of evaporation = 10 hours

Estimate the diffusion coefficient of carbon tetrachloride into air.

A6)

Molecular weight of CCl4 (A) and oxygen (B).

MA = 12 + 4(35.5) = 154

MB = 32

Partial pressure of CCl4 and O2 at the bottom and top is

pA1 = 33 mm Hg,          pB1= 760 – 33 = 727 mm Hg

pA2 = 0                            PB2 = 760 mm Hg

NA/A =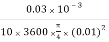

=

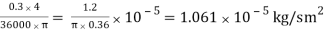
p = 1.01325  105 N/m2, T = 273 K,

y = y2 – y1 = 0.15 m

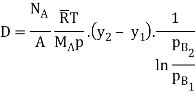
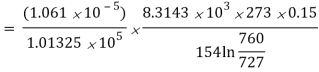
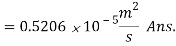
Q7) Calculate the rate of burning of a pulverized carbon particle, d0= 0.25 cm, in an atmosphere of pure oxygen at 1000 K and 1 atm pressure, assuming that a very large blanketing layer of CO2has formed around the particle. At the carbon surface, pCO2= 1atm, pO2 = 0, and at a very large radius, pCO2= 0 and pO2= 1atm. Take D = 0.4 m2/h.

A7)

Since C + O2  CO2, this is a case of equimolar counter diffusion. In spherical coordinates,

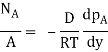
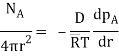
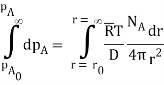
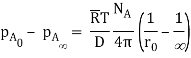
Since pA = 0, the burning rate of carbon is

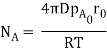
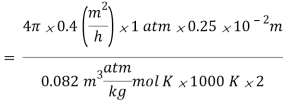
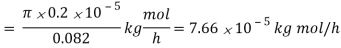
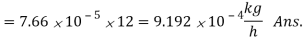
Q8) Explain Fick’s law of diffusion.

A8) Mass transfer by molecular diffusion is analogous to heat transfer by conduction or momentum transfer in laminar flow. Mass transfer by molecular diffusion may occur in a stagnant fluid or in a fluid in laminar flow. Like the Fourier’s equation of heat conduction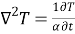, the concentration field of the diffusing species A is given by

∇2CA = 1/D  CA/t

Where CA is the concentration of component A in a mixture of A and B in kgmol/m3, t is the time in seconds and D is the mass diffusivity in m2/s.

For one-dimensional mass diffusion,

2CA/y2 = 1/D  CA/t

Where y is the distance in the direction of diffusion.

Like the conduction equation

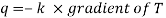
The mass transfer equation is

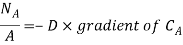
For one dimensional mass transfer

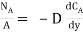…(1)

Where NA/A is the mass flux in kgmol/m2s. The negative sign appears because the concentration gradient is negative in the direction of mass transfer.

Equation (1) is called Fick’s law of diffusion, which states that the mass flux of a constituent per unit area is proportional to the concentration gradient.

Q9) Explain physical phenomenon of mass transfer.

A9)

• Consider a chamber in which two different gas species at the same temperature and pressure are initially separated by a partition. If the partition is removed without disturbing the fluid, both species will be transported by diffusion. Figure 6.1 shows the situation as it might exist shortly after removal of the partition.
• A higher concentration means more molecules per unit volume, and the concentration of species A (light dots) decreases with increasing x, while the concentration of B increases with x.
• Since mass diffusion is in the direction of decreasing concentration, there is net transport of species A to the right and of species B to the left.

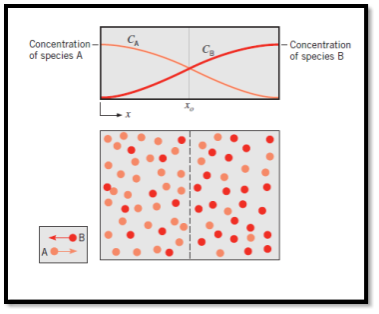
Fig: Mass transfer by diffusion

• The physical mechanism may be explained by considering the imaginary plane shown as a dashed line at xo. Since molecular motion is random, there is equal probability of any molecule moving to the left or the right. Accordingly, more molecules of species A cross the plane from the left, since this is the side of higher A concentration than from the right. Similarly, the concentration of B molecules is higher to the right of the plane than to the left, and random motion provides for nettransfer of species B to the left. After a sufficient time, uniform concentrations of A and B are achieved, and there is no net transport of species A or B across the imaginary plane.

Mass diffusion occurs in liquids and solids, as well as in gases. However, since mass transfer is strongly influenced by molecular spacing, diffusion occurs more readily in gases than in liquids and more readily in liquids than in solids.

Q10) What are similarities between heat and mass transfer.

A10) Heat transfer and Mass transfer are similar very similar to one another. Similarities between them can be explained by following key points.

• Heat transfer takes place by the virtue of temperature difference. Similarly, mass transfer takes place because of concentration difference between two points.
• Heat flows from high temperature to low temperature. Whereas, mass transfer takes place from high concentration to low concentration.
• Heat transfer by conduction is explained with the help of Fourier’s law which is given as

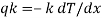
Where, qkis the rate of heat flux (a vector) in W/m2, dT/dx is the temperature gradient in the direction of heat flow x and k is the constant of proportionality

Mass transfer is explained with help of Fick’s law which is given as

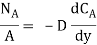
Where NA/A is the mass flux, 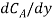is concentration gradient and D is constant of proportionality.

• Heat convection takes place by molecular diffusion whereas, mass convection takes place by mass diffusion.
• Heat convection equation is gives as

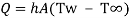
Where, Q is rate of heat transfer (W), A is area in m2, h is constant known as coefficient of convective heat transfer or film coefficient with unit W/m2K.

Mass convection equation is given as

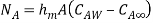
Where 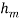is coefficient of mass convection, 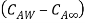represent concentration difference.

• Nusselt number, Reynold,s number and Prandtl number are governing constants of heat convection. They can be correlated as

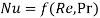
Likewise, Sherwood number, Reynold’s number and Schmidt number are governing constants in convection mass transfer which can be correlated as