M1
Unit 5Linear Algebra – Matrices system of linear equations.a) Reduce the following matrices into normal form and hence find it’s rank.(i)  (ii)
(ii)  (iii)
(iii) 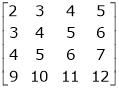 (iv)
(iv) 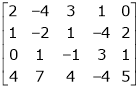 b) Solve the following system of equations(i)
b) Solve the following system of equations(i) 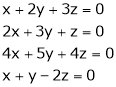 (ii)
(ii) 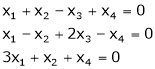 (iii)
(iii) 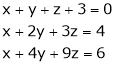 (iv)
(iv) 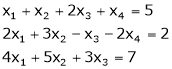 c) Find the value of
c) Find the value of 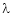 for which system of equations
for which system of equations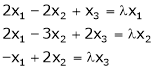 Can possess a non – trivial solution obtain the general solution for each realvalue of
Can possess a non – trivial solution obtain the general solution for each realvalue of 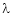 .d) Examine for liner dependence or independence of the following set of vectors.(i) (1, -1, 1), (2, 1, 1), (3, 0, 2)(ii) (1, 1, 1), (1, 2, 3), (2, 3, 8)(iii) (1, 3, 4, 2), (3, -5, 2, 6), (2, -1, 3, 4)(iv) (2, -1, 3, 2), (1, 3, 4, 2) (3, -5, 2, 2)(v) (3, 1, -4), (2, 2, -3), (0, -4, 1)If dependent find the relation between them.e) Is
.d) Examine for liner dependence or independence of the following set of vectors.(i) (1, -1, 1), (2, 1, 1), (3, 0, 2)(ii) (1, 1, 1), (1, 2, 3), (2, 3, 8)(iii) (1, 3, 4, 2), (3, -5, 2, 6), (2, -1, 3, 4)(iv) (2, -1, 3, 2), (1, 3, 4, 2) (3, -5, 2, 2)(v) (3, 1, -4), (2, 2, -3), (0, -4, 1)If dependent find the relation between them.e) Is 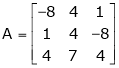 orthogonal. If not can be it converted in to an orthogonal matrix?f) Verify whether following matrix is orthogonal or not
orthogonal. If not can be it converted in to an orthogonal matrix?f) Verify whether following matrix is orthogonal or not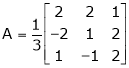 if so find A-1.g) Show that
if so find A-1.g) Show that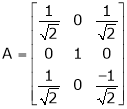 Is orthogonal matrix.
Is orthogonal matrix.
 (ii)
(ii)  (iii)
(iii)  (iv)
(iv) 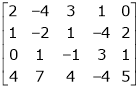 b) Solve the following system of equations(i)
b) Solve the following system of equations(i) 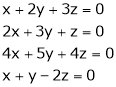 (ii)
(ii) 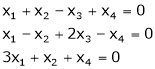 (iii)
(iii) 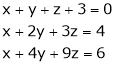 (iv)
(iv) 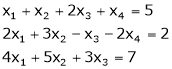 c) Find the value of
c) Find the value of 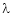 for which system of equations
for which system of equations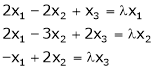 Can possess a non – trivial solution obtain the general solution for each realvalue of
Can possess a non – trivial solution obtain the general solution for each realvalue of 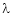 .d) Examine for liner dependence or independence of the following set of vectors.(i) (1, -1, 1), (2, 1, 1), (3, 0, 2)(ii) (1, 1, 1), (1, 2, 3), (2, 3, 8)(iii) (1, 3, 4, 2), (3, -5, 2, 6), (2, -1, 3, 4)(iv) (2, -1, 3, 2), (1, 3, 4, 2) (3, -5, 2, 2)(v) (3, 1, -4), (2, 2, -3), (0, -4, 1)If dependent find the relation between them.e) Is
.d) Examine for liner dependence or independence of the following set of vectors.(i) (1, -1, 1), (2, 1, 1), (3, 0, 2)(ii) (1, 1, 1), (1, 2, 3), (2, 3, 8)(iii) (1, 3, 4, 2), (3, -5, 2, 6), (2, -1, 3, 4)(iv) (2, -1, 3, 2), (1, 3, 4, 2) (3, -5, 2, 2)(v) (3, 1, -4), (2, 2, -3), (0, -4, 1)If dependent find the relation between them.e) Is 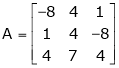 orthogonal. If not can be it converted in to an orthogonal matrix?f) Verify whether following matrix is orthogonal or not
orthogonal. If not can be it converted in to an orthogonal matrix?f) Verify whether following matrix is orthogonal or not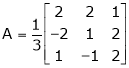 if so find A-1.g) Show that
if so find A-1.g) Show that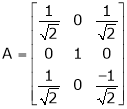 Is orthogonal matrix.
Is orthogonal matrix. 0 matching results found

