M2
Unit VIMultiple Integrals and their Applications Evaluate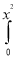 
ey/x dy dx. Evaluate x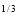
y
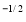(1 – x –y)
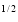dx dy. Evaluate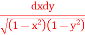 
: Evaluate e–x2 (1 + y2) x dx dy. Evaluate y dx dy over the area bounded by x= 0 y =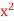 
and x + y = 2 in the first quadrant Evaluate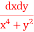 
over x 1, y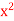 
Evaluate (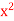
+ 
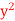) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2. Change the order of integration for the integral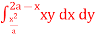 
and evaluate the same with reversed order of integration. Evaluate I =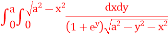 
10. Express as single integral and evaluate dy dx + dy dx.11. Evaluate
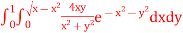12. Sketch the area of double integration and evaluate 
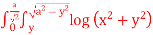dxdy13. Evaluate r4 cos3 dr d over the interior of the circle r = 2a cos 14. Evaluate r sin dr d over the cardioid r = a (1 – cos ) above the initial line. 15. Find the area between the curves 
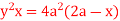and its asymptote.16. Show that the area of curve 
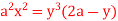is 
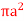17. Find the Area common to the two circle 
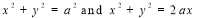18. Evaluate 
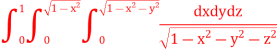19. Evaluate 
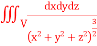Where V is annulus between the spheres 
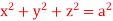20. Evaluate 
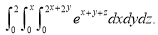21. Evaluate 
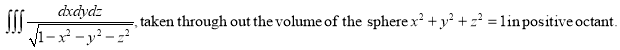22. Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane 
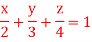23. 
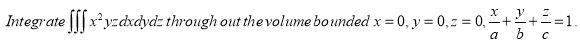24. 
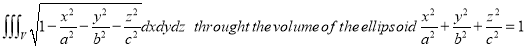25. If the density at any point of a non uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then find the mass of lamina.26. Find The Mean Value of 
Over the positive octant of the Ellipsoid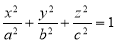 
27. A lamina bounded by the parabolas 
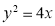and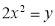 
has a variable density 
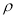Given by 
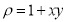. Prove that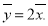 
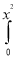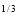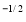ey/x dy dx.y (1 – x –y) 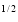dx dy.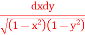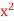and x + y = 2 in the first quadrant 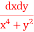over x 1, y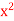 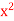+ 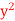) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2. 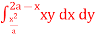and evaluate the same with reversed order of integration.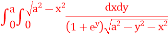10. Express as single integral and evaluate dy dx + dy dx.11. Evaluate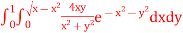12. Sketch the area of double integration and evaluate 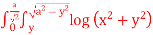dxdy13. Evaluate r4 cos3 dr d over the interior of the circle r = 2a cos 14. Evaluate r sin dr d over the cardioid r = a (1 – cos ) above the initial line. 15. Find the area between the curves 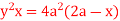and its asymptote.16. 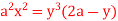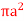Show that the area of curve is 17. Find the Area common to the two circle 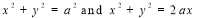18. Evaluate 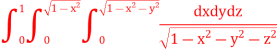19. Evaluate 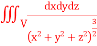Where V is annulus between the spheres 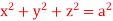20. Evaluate 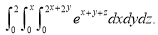21. Evaluate 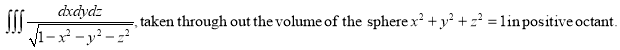22. Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane 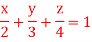23. 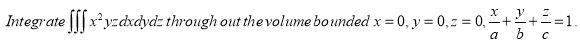24. 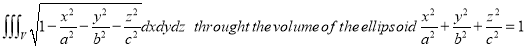25. If the density at any point of a non uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then find the mass of lamina.26. Find The Mean Value of Over the positive octant of the Ellipsoid 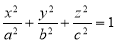27. A lamina bounded by the parabolas 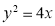and 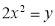has a variable density 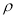Given by 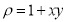. Prove that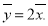 
0 matching results found