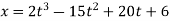Q. No. | Question Description | |||||||||
| Rectilinear Motion – Variable Acceleration | |||||||||
1 | A particle moves along a straight line with an acceleration a = (4t2 – 2), where a is in m/s2 and t is in s. when t = 0, the particle is at 2 m to the left of origin and when t = 2 sec the particle is at 20 m to left of origin. Determine the position of particle at t = 4 sec. | |||||||||
2 | The acceleration of particle as it moves along a straight line is given by a = (2t - 1), where t is in s. If S = 1m and v = 2 m/s when t = 0, Determine the particle velocity and position when t= 6 sec. | |||||||||
3 | A sphere is fired into a medium with a initial velocity of 27m/s. If it experience a deceleration of a = (-6t2) m/s2. Determine distance travelled before it stops. | |||||||||
4 | A body moves in straight line, its acceleration is given by a = 90 − 6x 2 where a is in m/sec2 & x in meters. The particle starts with no velocity at position x=0. 1) Find velocity when x=0 2) The position where velocity is zero again 3) The position when velocity maximum | |||||||||
5 | The Y Coordinate of a particle in curvilinear motion is given by y = 4t3 - 3t, where y is in meters and t in second. Also the particle has an acceleration in the x direction given by x = 12t m/s2. If the velocity of the particle in the x direction is 4 m/s when t = 0, calculate the magnitudes of the velocity ‘V’ and acceleration ‘a’ of the particle when t = 1 s. | |||||||||
6 | A position of Particle moving in straight line is expressed by | |||||||||
| Rectilinear Motion – Constant Acceleration | |||||||||
1 | An auto starts from rest and reaches a speed of 54 kmph in 15 seconds. The acceleration increases uniformly from zero for the first 9 sec. After which it reduces uniformly in next 6 sec. Find displacement in the 15 sec interval. | |||||||||
2 | Two trains P and Q are 190 m and 160m long moving in opposite directions on parallel tracks. The velocity of the shorter train is three times that of larger one. If the trains take 5 s to pass each other, determine the velocity of each train. | |||||||||
3 | A car comes to complete stop from an initial speed of 50 kmph in a distance of 100 m. With the same constant acceleration, what would be the stopping distance s from an initial speed of 70 kmph? | |||||||||
4 | A motorcycle patrolman starts from rest at A, two seconds after a car, speeding at the constant rate of 120 kmph, passed point A. If the patrolman accelerates at the rate of 6 m/s2 until he reaches his maximum permissible speed of 150 km/h, which he maintains, calculate the distance s from point A to the point at which he overtakes the car. | |||||||||
5 | A car initially moving with 50 m/s travels 80 m before it stops after applying the brakes. Now with same rate of acceleration, if a car is moving with 70 m/s, then what will be the distance travelled by car before coming to rest. | |||||||||
Rectilinear Motion- Motion Under Gravity | ||||||||||
1 | A stone is dropped from top of tower 50 m high. At the same time another stone was thrown vertically upward with a velocity of 25 m/s, when and where they cross with each other. | |||||||||
2 | A child throws a tennis ball vertically upwards at 7.7 m/ s from ground level. Assuming that no resistance forces act on the ball, so that it moves only under the influence of gravity (g = 9.81 m/s2), what is the maximum height the tennis ball reaches? | |||||||||
3 | A ball is projected vertically upward with a velocity of 9.81 m/s. Determine the maximum height travel by the ball, the velocity at which it strikes the ground and total time of journey. | |||||||||
4 | A child throws a tennis ball vertically upwards at 7.7 m/ s from ground level. Assuming that no resistance forces act on the ball, so that it moves only under the influence of gravity (g = 9.81 m/s2), what is the maximum height the tennis ball reaches? Also find time taken to reach maximum height. | |||||||||
5 | At t = 0, bullet A is fired vertically with an initial velocity of 450 m/s. When t = 3 s, another bullet B is fired upward with a muzzle velocity of 600 m/s. Determine the time t, after A is fired, as to when bullet B passes bullet A. At what altitude does this occurs? | |||||||||
6 | A stone which is thrown vertically upward reaches maximum height of 60 m. Determine initial velocity of stone with which it was thrown, and time taken to reach maximum height. | |||||||||
Rectilinear Motion- Motion Diagrams | ||||||||||
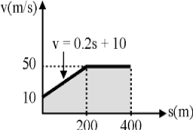
1 | The v – s diagram for motion of a car is given. Plot a – s diagram and determine the time required for the car to reach the position s = 400 m. |
| ||||||||
| Rectilinear Motion- Relative Velocity | |||||||||
1 | Two ships leave a port at the same time. The first, ship A steams 300 North-East at 16 kmph & the second ship B steams 40° South of East at 12 kmph. Determine the relative velocity of ship B with respect to ship A. | |||||||||
2 | At an instant ship A is streaming due East at 20 km/h and ship B at that instant is 80 km due South and is streaming at 16 km/h due N-W. Determine: (a) VB/A, (b) shortest distance between them, (c) time to attain the shortest distance. | |||||||||
| Rectilinear Motion- Dependent Motion | |||||||||
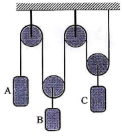
1 | If a block A of the pulley system is moving downward at 2 m/s while block C is moving down at 6 m/s, determine the relative velocity of block B with respect to C. Refer Fig. |
| ||||||||
| Cartesian/Rectangular Co-ordinates | |||||||||
1 | The curvilinear motion of a particle is given by Vx = (50 - 16t) m/sec and y=(100-4t2) m. Determine the Velocity and Acceleration when the position y = 0 is reached. | |||||||||
| Tangential and Normal Co-ordinates/Path Co-ordinates/ Path Variables | |||||||||
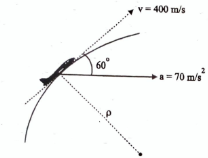
1 | At a given instant the plane has a speed of 400 m/s and acceleration of 70 m/s2 acting as shown in Fig. Determine the rate of increase in plane’s speed and radius of curvature of the path. |
| ||||||||
2 | Determine the distance travelled and time taken by the car starting from rest, moving on a circular curve having radius of 275 m, and accelerates at a constant tangential acceleration of 1.0 m/s2 and total acceleration of 1.4 m/s2. | |||||||||
3 | A train when enters in to curved track decreases its speed from 25 m/s to 20 m/s in 8 seconds. Determine total acceleration of train at a speed of 20 m/s if radius of curvature of tack is 800 m. | |||||||||
4 | A particle travels a curved path of radius of 600 m with a speed of 108 kmph and a tangential acceleration of 4 m/s2. Determine the total acceleration of particle. | |||||||||
5 | A car initially moving with 100 kmph enters the curved portion on the road. It decelerates its speed to 50 kmph within 12 sec. Determine the radius of curvature of road surface at a point where car is having speed 50 kmph if Total Acceleration of car is 4 m/s2. | |||||||||
| Radial and Transverse Co-ordinates/Polar Co-ordinates/Circular Motion | |||||||||
1 | A particle position is described by co–ordinates r = (2 Sin2θ) meter & θ = (4t) rad, where ‘t’ is in seconds. Determine the Radial and transverse components of velocity and acceleration when t = 1 sec. | |||||||||
2 | The car travels around the circular track such that its transverse component is θ = (0.006 t2) rad, where t is in seconds. Determine the car’s radial and transverse components of velocity and acceleration at the instant t = 4 s. | |||||||||
3 | An outdoor track is 126 m in diameter. A runner increases her speed at a constant rate from 4.2 to 7.2 m/s over a distance of 28.5 m. Determine the total acceleration of the runner 2 sec after she begins to increases her speed. | |||||||||
4 | A particle moves in a circular path of radius 0.4 m. Calculate magnitude of acceleration a of the particle if its speed is 0.6 m/s but it increasing at the rate of 1.2 m/s each second. | |||||||||
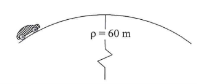
5 | If the crest of the hill has a radius of curvature = 60 m, determine the maximum constant speed at which the car of weight 17.5 kN can travel over it without leaving the surface of the road. |
| ||||||||
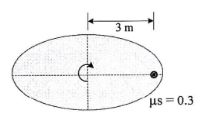
6 | The man has a mass of 80 kg and sits 3 m from the center of the rotating platform. flue to the rotation his speed is increased from rest by 0.4 m/s2. If the coefficient of static friction between his clothes and the platform is, μs = 0.3, determine the time required to cause him to slip. Refer Fig. |
| ||||||||
7 | The small 0.6 kg block slides on a smooth circular path of radius 3 m in the vertical plane. If the speed of the block is 5 m/s as it passes point A and 4 m/s as it passes point B, determine the normal force exerted on the block by the surface at each of these location. Refer Fig. | | ||||||||
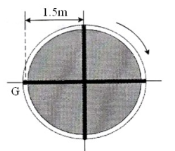
8 | A girl having mass of 25 kg sits at the edge of the merry go-round so her centre of mass G is at a distance of 1 .5 m from the centre of rotation as shown in Fig. Neglecting tangential component of acceleration, determine the maximum speed which she can have before she begins to slip off the merry go-round. The coefficient of static friction is μs= 0.3. Use Newton’s second law of motion. |
| ||||||||
| Radius of Curvature | |||||||||
1 | A particle starts from rest at origin and the rectangular components for the particle are ax = 6t and ay = 60 - 15t . Determine the radius of curvature of the path. | |||||||||
| Projectile Motion | |||||||||
1 | A projectile is launched with a speed of V0 = 25 m/s at an angle of θ = 30° with horizontal as shown in Fig. Determine the maximum distance travelled by projectile along horizontal and Vertical Direction. Also find Time of Flight |
| ||||||||
2 | A Missile is fired from nozzle with an initial velocity 50 m/s having inclination 25° w.r.t. horizontal. Determine (i) time taken by missile to reach maximum height and (ii) horizontal distance covered by missile when it reaches maximum height. | |||||||||
3 | A baseball player throws baseball with a horizontal velocity vo. Knowing that the height varies between 775 mm and 1050 mm, determine (a) the range of |
| ||||||||
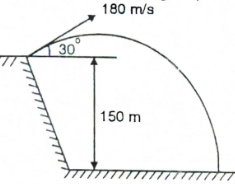
4 | A projectile is fired from the edge of a 150 m cliff with an initial velocity of 180m/sec at an angle of 30° with the horizontal. Neglecting air resistance, find the horizontal distance from the gun to the point, where the projectile strikes the ground and the greatest elevation above the ground reached by the projectile. Refer Fig. |
| ||||||||
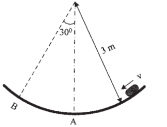
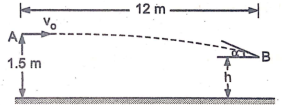
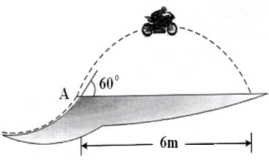
5 | During a race the dirt bike was observed to leap up off the small hill at A at an angle of 60° with the horizontal as shown in Fig. If the point of landing is 6 m away, determine the approximate speed at which the bike was travelling just before it left the ground. |
| ||||||||
6 | A baseball is thrown downward from a 15 m tower with an initial speed of 5 m/s. Determine the speed at which it hits the ground and the time of travel. | |||||||||
7 | A cricket ball shot by a batsman from a height of 1.8 m at an angle of 300 with the horizontal with a velocity of 18 m/s is caught by a fielder at a height of 0.6 m from the ground. Determine the distance between the batsman and fielder. | |||||||||
8 | A cricket ball thrown by a fielder from a height of 2 m at an angle of 450 to the horizontal with an initial velocity of 25 m/s hit the wickets at the height of 0.6 m from the ground, find distance of fielder from the wickets. | |||||||||
9 | A cricket ball shot by a batsman from a height of 2.0 m at an angle of 30 with the horizontal with a velocity of 20 m/s is caught by a fielder at a height of 0.8 m from the ground. Determine the distance between the batsman and fielder. | |||||||||
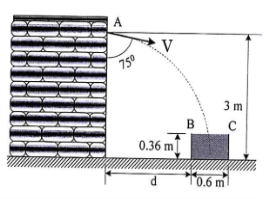
10 | Water flows from a drain spout with an initial velocity of 75 m/s at an angle of 750 with the vertical as shown in Fig. Determine the range of values of the distance d for which the water will enter the trough BC. |
| ||||||||