|
|
|
|
|
|
|
|
|
|
|
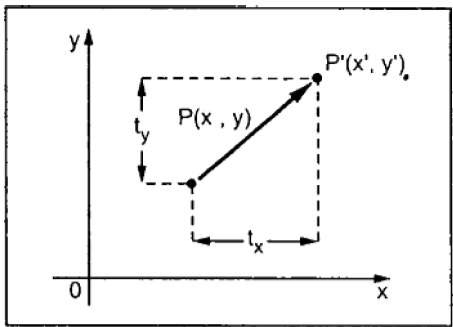
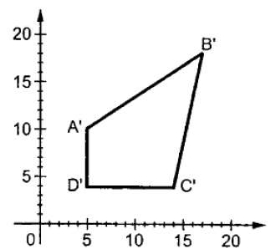
The figure 2.2.1 shows the translation process.
Fig. no. 2.2.1 In the figure, X’=X+tx Y’=Y+ty The pair (tx, ty) is called the translation vector or shift vector.
P = X
T = tx ty
= X + tx Y ty |
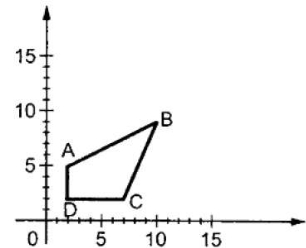
If the value assigned to the scaling factor S is greater than 1 then the size of the abject will increased.
Fig.no. 2.2.2
Let assume that the original coordinates are X and Y and the scaling factors are (Sx, Sy). The mathematics representation of the scaling represented as shown below: X’=X * Sx And Y’=Y * Sy
P= X and S= Sx Y Sy
= X * Sx Y Sy |
The rotation is achieved by using the following rotation equation: X’=X * cos Ꙫ - Y * sin Ꙫ Y’ =X * sin Ꙫ + Y * cos Ꙫ In matrix for, the clockwise rotation represented as shown below: X’ = cos Ꙫ - sin Ꙫ * X Y’ sin Ꙫ cos Ꙫ Y In matrix for, the anti-clockwise rotation represented as shown below: R= cos Ꙫ sin Ꙫ -sin Ꙫ cos Ꙫ The homogeneous coordinates will be represented as : X’ = cos Ꙫ - sin Ꙫ 0 * X Y’ sin Ꙫ cos Ꙫ 0 Y 1 0 0 1 1 |
|