Computer Graphics
UNIT - 6Virtual Reality
Q1) What is Curve? Explain curve generation.A1) A curve is an infinite large set of points.Each point has two neighbors except endpoints.The classification of the curve is as follows:Explicit curve Implicit curve Parametric curve
Curve GenerationCurves are used to make the high resolution graphics.At fixed resolution the small polylines are allowed to create graphics which appears smooth.The smoothness is not preserved when scaled at high resolution also it requires more amount of storage for any high resolution image.Curves can be stored easily and scaled at any resolution without losing smoothness.The curves can be easily specify in real world objects.The curves are specified by parametric equation used in graphics.Equations that are used in curve generation,Y= fy(u) and x= fx(u) Q2) Write Interpolation used in curve generation.A2) The interpolation is filling in frames between the key frames.It uses the polynomial interpolation to draw images semi automatically.It is a generating principle which enables to model connected curve segments from the discrete ordered sets of points in the extended space. Q3) Explain Interpolating algorithms:Linear interpolation Hermite interpolation Cubic interpolation A3) Linear InterpolationThis is a simple method of interpolation.In this the values are getting at position in between the data points.The points are joined by straight line segment in simple interpolation.Each line segment can be interpolated independently.The parameter mu used to define the value on the interpolated line.Following figure 6.1.3 (a) shows the linear interpolation.
Fig. no. 6.1.3 (a)Hermite interpolationIt is a polynomial unction that is used for interpolating data points.The Hermite interpolating polynomial is same as newton interpolating polynomial.The interpolating polynomials are calculated by divided differences.The Hermite interpolation can be calculated without using divided differences.The observed value can be unknown to the Hermite interpolation.Following figure 6.1.3 (b) shows the representation of the Hermite interpolation.
Fig. no. 6.1.3 (b)Cubic interpolationIt is also a simple interpolation method which offers the continuity between the segments.It requires more than two points to join the segment but also it requires two endpoints on either side of them.The function required four points.Following figure 6.1.3 (c) shows the cubic interpolation.
Fig. no. 6.1.3 (c) Summary:The interpolation is filling in frames between the key frames.The interpolating algorithms are as follows:Hermite interpolation Linear interpolation Cubic interpolation Q4) Explain Interpolating Polygons in short.A4) The polygon interpolation is complex than the interpolation of simple values like numbers.As the data being interpolated becomes more complex.The interpolation of polygon is interesting.Following are some functions of interpolation:Initial Final P indicates position of value being returned Where p=0 which returns the initial value and p=1 which indicates the final valueThe mathematical notation is given as,V= Vinitial * (1-p) + Vfinal * pThe problem is solved with two equal size of polygons.The problem can be broken down into interpolating series of points.Each point can be broken down into interpolating two numbers.Following figure 6.1.4 shows the representation of interpolation of polygon.
Fig. no. 6.1.4Q5) Explain B-Spline Curve with properties.A5)
Properties of B-spline curve:The sum of B-spline basis function for any parameter value is 1. For all parameter values each basis function is positive or 0. Each basis function have one maximum value except for k=1. The number of vertices in polygon is equal to the maximum order of the curve. The degree of B-spline polynomial is independent on the number of vertices of polygon. B-spline curve allows the local control over the curve surface. It explicit the variation diminishing property. It follows the shape of the defining polygon. Q6) Explain Bezier Curve with properties.A6) The Bezier curve are developed by French engineer Pierre Bezier.
Properties of Bezier curve:It follows the shape of the control polygon which consist of segment joiing the control points. It always passes through first and last control point. The convex hull contains the Bezier curve with defining control point. The degree of the polynomial defining the curve segment is 1 less. The Bezier curve follows the polynomial control points. Q7) What is Fractal in computer graphics?A7) The fragmented geometric shape that can be split into parts.Fractal is the complex picture that is generated by computer from one formula.Fractals are created using iteration.The formula of fractal repeats again and again with slightly different values.The figure 6.1.7 represents as different shapes of fractals.
Fig. no. 6.1.7 Q8) Explain Classification of Fractals.A8) The fractals can be classified as:Self-Similar Fractal:These fractal are scaled down the version of entire object.The overall fractals are scaled by the applying the scaling parameter s to the initial shape.It is all over the user to choose the same scaling factor s for all subparts or different scaling factors for different scaled down parts.In sub class of self-similar fractal the user can use the random variation to the scaled down sub parts.This fractals are used to model tree, shrubs and other plants.Self-Affine Fractal:The self-affine fractals are scaled down with different scaling parameters as Sx, Sy and Sz in different coordinate direction.We can apply random variations to obtain self-affine fractals.This fractals are used to model water, clouds and terrain.Invariant:The invariant fractals uses the non-linear transformation.It includes self-squaring function such as Mandelbrot set.It uses inversion procedure to form squaring function and self-inverse fractals. Q9) Explain fractal dimension and fractal surfaces with dimensions.A9) Fractal DimensionAs the scale changes the ratio of change in detail by the quantifying complexity.The index for characterizing fractal patterns are known as fractal dimension.The fractal dimensions can be count as empirically and theoretically.The categorization a broad spectrum of objects ranging from the abstract.It is a practical phenomenon. Fractal Dimension And SurfacesIt is a measure of fractal dimension of surface geometric complexity.It can take any non-integer value between 2 and 3.Normally the dimension of surface is 2.The fractal dimension get increase with its greater amount of complexity or roughness. Q10) Explain Hilbert Curve in short.A10) It is also known as Hilbert space filling curve.It is continuous fractal space filling curve.It is developed by German mathematician David Hilbert.As it is a space filling algorithm its Hausdroff dimension is 2.It has unit square image which has dimension as 2.Its graph is compact set homeomorphism to the closest interval.Following figure 6.1.7 (a) shows the Hilbert curve.
Fig. no. 6.1.7 (a) Q11) Explain Snowflake Fractal Generation.A11) It is known as Koch curve, Koch star or Koch island.It is mathematical curve and described earliest than the other fractals.Following are some step to create snowflake fractal.Step 1: draw a triangle.Step 2: divide each side in three equal parts.Step 3: draw an equilateral triangle on each middle part.Step 4: divide each outer side into three and second generation of triangles covers the bit of first.Step 5: repeat the process to get the snowflake fractal.Following figure 6.1.7 (b) shows the snowflake fractal.
Fig. no. 6.1.7 (b) Q12) What is Fractal lines and surfaces?A12) The value of the Fourier dimension depends on the smoothness of fractal surface.The large fractals shapes or global topology is determined by random number generating algorithm.The fractal surface has roughness factor.The value of roughness factor depends on probe size and fractal dimension.
|
|
|
|
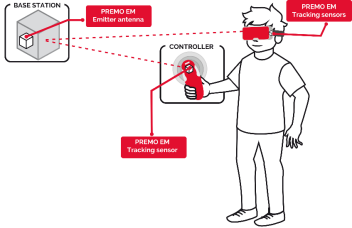
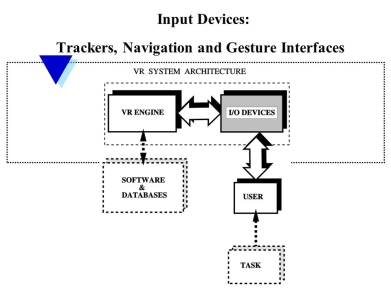
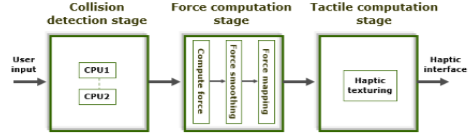
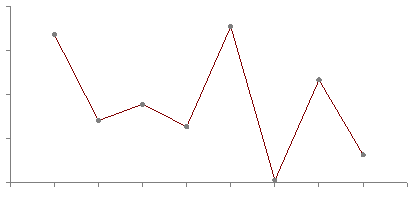
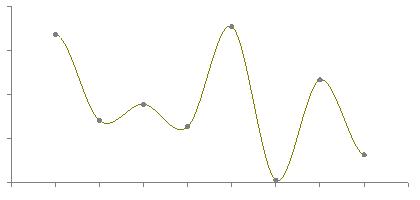
B-spline curve overcomes the limitation of Bezier curve as Bezier curve has limited flexibility. It is a special case of Berstein basis. It is non-global method. It consists of linear combination of control points Pi and B-spline basis function Ni. The mathematical representation of B-spline curve is, C(t) = ∑ Pi * N (i, k) (t) Where summation limitation is n to i=0 and n >= k-1, t belongs to (tk - 1, tn + 1) Here k is order of polynomial segments of B-spline curve. N(i,k)(t) it is an normalized B-spline blending function. Following figure 6.1.5 shows the B-spline curve.
Fig. no. 6.1.5 |
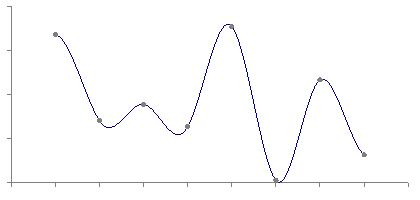
The Bezier curve is generated under the control of other points. To generate the Bezier curve approximate tangents are used by using control points. The mathematical representation of Bezier curve is, ∑ Pi * B ni (t) where summation from n to k=0 Pi is the set of points and B(t) is berstein polynomials as B(t)= (n, i) (1 - t) n-I * ti The simple beizer curve is a straight line from P0 to P1. A quadratic Bezier curve has three control points. A cubic Bezier curve is determined by four control points. Following figure 6.1.6 represents the Bezier curve.
Fig. no. 6.1.6 |
|
|
|
Q13) Explain the concept of Interactive Graphics & usage of the tools of computer graphics.3D StudioMayaA13)3 dimensional computer graphics is the contrast of 2 dimensional computer graphics.The 3D computer graphics used to represent the geometric data which is stored in computer for use of calculations.It is also used to render the 2D images.The result of image is stored for viewing later or display in real time.The interactive graphics uses tools of computer graphics as 3D studio and Maya. 3D Studio:The 3D studio is a studio where 3 dimensional work is created.It is also known as 3D studio max which is a animation software package.It is a professional 3D computer graphics program.It used to develop 3D animations, models, games and images.The Autodesk media and Entertainment is developed by 3D studio max.3D studio max has modelling capabilities and flexible design architecture.It is also used for Microsoft windows platform. Maya:It is an Autodesk 3D computer graphics software application.It runs on Windows, Linux as well as macOs.The Alias system corporation develops the Autodesk Maya.It is used to create assets for interactive 3D applications, animated films, TV series, video games, etc. Q14) Explain Virtual Reality as Fundamental Concept.A14) It is mimicry of real world beyond the flat monitor which gives the 3D visual experience.Virtual reality is the experience that is similar to real world or it can be different from the real world. It is used in various field as medicine, entertainment, education, design and training, etc.It often used in marketing buzzword for compelling interactive video games or 3D movies and television programs. Q15) Explain in short Three I’s Of Virtual Reality.A15) Three I’s of virtual realityVirtual reality is based on following three I’s:Immersion:It helps to feel the real audience as virtually.As the immersion helps in visualization or branded projects to adjust formatting and to find exciting way to take into new world for people.Immersion gives the real time perception of being present physically in virtual environment.It also helps to interact with or without disruption.It translates directly into increased comfort. The immersion shows the sympathy towards the brand providing such a real experience.Immersion is the simulation of computer graphics.It creates the real world realistic and becomes interactive.It is the part of screen where action performs. InteractionInteraction is the action that performs on the user’s input.Interaction is found with functionality such as user’s input with gesture, verbal commands, head movement tracking, etc.As example, the product in virtual clothing store can be interacted and manipulated using controllers or by gazing at certain points in the created environment.By interaction the experience goes to the next level.It works from passive observation to active participation.The device tracks the interaction of user in virtual world from which the tool understand user’s needs and it influence user in buying decision process.Interaction becomes synthesized not static. ImaginationIn virtual reality the imagination used to perceive non-existent things and creates illusion of them being real.Virtual reality is the medium to tell story and experience it.It also helps in marketing to show the number of possibilities.The human imagination occurs in virtual environment.It creates the virtual world in front of human mind.As the imagination occurs the problems solving ability is also increasing in virtual environment.Following figure 7.1 shows three types of I used in virtual reality.
Fig. no.7.1 Summary:There are three I’s in the concept of virtual reality.Immersion Interaction Imagination Q16) Write short note on Classic Components of VR Systems.A16) This section shows the overview of VR system from hardware to software to human perception to understand working of entire VR system.Following are the components that are used in VR system.Hardware VR device Software Audio Human perception HardwareThe hardware of VR works on the human motion then hardware produce stimuli which overrides the senses of the user.This process is occurred by sensors for tracking motions of user such as button presses, controller movements, and eye and other body part movement, etc.It also considers the physical surrounding world as it is engineered hardware and software which not constitutes the complete VR system.The user’s interaction and user both are equally important for hardware.The hardware of VR is sensor which converts the energy from signal to electrical circuit. Hence it is acting like a transducer.The sensor are receptors to collect the energy for conversion where user get sense about his eyes and ears for the same purpose.The user moves with physical world which is having his own configuration space which can be transformed or configured correspondingly. VR DeviceThe device that is hardware product used for VR technology to happen.Basically the inputs are received by the user and his surrounding with appropriate view of the world which renders to display for VR experiences.Some kind of key components are used for VR system as given below:Personal Computer/ Console/ smartphone The PC or console or smartphone is required for creation of content and production of significant computing power.As the inputs and outputs are collected sequentially by the computer.Therefore the PCs are important for the VR system.The VR content is perceive by the user or user that view inside so it is equally important other hardware. Input device Input devices are used to give the immersion to the user.It determines the way of user communication with computer.The input devices are helping user to interact with VR environment to make it intuitive and natural as possible.But in current state it is not advanced enough to support this yet.Following are some input devices used in VR system.Joystick Force balls/tracking balls Controller wads Data gloves Track pad On-device control buttons Motion tracker Bodysuits Treadmills Motion platforms (virtual omni) Output device It is a device that can actually sense organs.It creates an immersive feeling in VR environment.It is used to present the VR world to the user.It uses the visual, auditory or haptic displays to present the VR system.In current situation the output devices are also underdeveloped due to the current state of art VR system is not allow to stimulate human senses perfectly.Some are the devices are used for audio or the haptic information.SoftwareAfter the coordination of input output devices the underlying software is also equally important.It helps to manage I/O devices, analyzing incoming data and also to generate proper feedback.As the applications are complex or time critical then software must be there to manage it.The input must be handle timely and sent to the output display to prompt the feeling of immersion in VR system.The process is start with SDK (Software Development Kit) from VR headset vendor and build their own VWG from scratch.SDK includes the basic drivers, an interface to access tracking data and call graphical rendering libraries.The readymade VWG are used for particular VR experiences and has option to add high level scripts. AudioIt is equally important as uses senses and to achieve immersion.It is technically may not be complex as visual components.Mostly virtual reality provides the headsets to users with option to use their own headsets in conjunction with headset.The audio in VR works as positional or multispeaker audio which gives the 3D world immersion.Positional audio is the way of seeing with ears used in VR to gain the attention of users and to give the information that cannot be shown visually. Human PerceptionTo achieve the human perception it needs to understand the physiology of human body.Optical illusion is important to achieve maximum human perceptual without side effects.There are different stimulus, receptor and sense organ of human are used to sense a human.In VR the human senses are fooled is important to create immersion or stimulate the real world in front of human.The human touch, hearing and other senses are followed by the human brain which gives the most of information to the VR to create a vision.In VR, the system synchronization of all stimuli with user’s actions are responsible for proper functioning of VR. Q17) Write down Applications Of VR Systems.A17) The Virtual Reality is described as the computer generated environment where user can interact and explore with.The user immersed in that world and the brain is triggered to think about the what someone is seeing in virtual world is real.Following are some applications of VR used in various fields:Automotive industry Healthcare Retail Tourism Real estate Architecture Gambling Learning and development Recruitment Entertainment Education Sports Arts and design Q18) Explain 3D Position Trackers And Its Types.A18) The head mounted display, controller and other body parts within space is detected by the positional tracking at its precise position.The VR is used to stimulate the perception of human.In 3 dimensional space the illusion is not break because of accurate and precise positional tracking being paramount.There are various methods of tracking the position and orientation of the display have been developed to achieve.The sensors tracked the signal from transmitters on or near the tracked objects and send the data to computer to maintain approximation of their physical location.The physical location can be identify and defined by using one or more coordinating system such as Cartesian rectilinear system, spherical polar system and cylindrical system.The movement controls and monitoring done by many interfaces which are designed for it.The positional tracking system is working to provide seamless user’s experience as shown in figure 7.2.
Fig. no. 7.2Following are the types of virtual 3D positional tracking.Wireless TrackingThe wireless tracking system is same as GPS system but works in both indoor and outdoor.It uses set of anchors which are placed around the perimeter of the tracking space and one or more tags that are tracked.It is also known as indoor GPS. Optical Tracking The computer vision algorithm is used in optical tracking.The cameras are used to tracked the position and orientation placed around the headsets.It works on stereoscopic human vision technique. Inertial TrackingAccelerometer and gyroscopes are used in inertial tracking system.The linear acceleration is measured by the accelerometer.Angular velocity is measured by gyroscope.The MEMs technology is used in modern inertial tracking system.It can track fast movements elated to other sensors.It is capable to give update on high rates. Acoustic Tracking The echolocation technique is used for acoustic tracking system.As naturally animal is found by device position followed by acoustic tracking.This technique is used to identify the objects or device position by echolocation.It gives accurate measurement of coordinates and angles.It is easy to produce and cheap to buy.It does not uses the electromagnetic interference. Magnetic TrackingIt follows the Theremin principle.The electromagnetic sensors are used to measure the intensity of inhomogeneous magnetic fields.It is suitable for fully immersive virtual reality displays.The user needs to be close to base emitter.It has lot of errors and jitter because of frequent calibration requirements. Q19) Analyze Navigation and Manipulation Interfaces.A19) Navigation is moving object from one place to other place within environment.The combination of travel with wayfinding and travel without wayfinding is used in navigation.It allows relative position control of virtual objects.The direct manipulation uses shadows, perspective, occlusion and other 3D techniques.It minimizes the number of navigation steps for users to accomplish their task.It avoids unnecessary visual clutter, distraction, contrast shifts and reflections.In Navigation and Manipulation Interfaces the user enable to construct visual groups to support spatial recall.Following figure 7.3 shows the input devices used in VR system.
Fig. no. 7.3 Q20) Explain Gesture Interfaces.A20) User usually uses the keyboard and mouse to interact with computer.The conventional keyboard and mouse interfaces decreases the level of immersion.As the manipulation method does not resemble actual action in reality.The gesture interface is used for the navigation in 3D space.It is suitable for HMD based virtual environment.The Kinect Depth Camera is used to capture and recognize the gesture in real time.The gesture interface is more preferable than conventional keyboard and mouse for obtaining a high level of immersion. Q21) Explain in short following Graphics Displays:A21) HMD And CAVE, Sound Displays, Haptic FeedbackHMD And CAVEHMDHMD requires distortion and color correction.HMD is completely immersive. There are 100 degrees of field view in HMD.The disembodies and isolating is presence of HMD.Only single user can use the HMD.In HMD the movement is limited due to isolation, tether and small tracked volume. CAVECAVE has perfect pixels.It is immersive but not as HMD.It has 170 degrees field of view more than HMD.It is excellent and can see own body.The CAVE is completely wireless, precise tracking.It can move around freely in user volume.The multiple viewers, one tracked user can handle CAVE.It has lightweight glasses and wireless. Sound DisplaysThe interactivity, immersion and perceived image quality are the role play of sound display.It is equally important in movies and video games.There are sound dimensions as mono, stereo and occlusion.Some are the sound display hardware such as offload computational load, convolved, Audigy. Haptic FeedbackIt is a touch to communicate with users.The haptic feedback is for example mobile phone vibrates on touch and rumble in game control.The device communicates with predominantly by sight and hearing as human having many senses to communicate.The haptic feedback uses to stimulate the sense of touch.As human touches to the computer same with computer also can touch to the user by haptic feedback.It is a mode of communication not a technology or application. Q22) Write short note on Rendering Pipeline as Graphics Rendering Pipeline.A22) Graphics rendering Pipeline is used to describe steps to be performed to render a 3D scene to 2D screen.It is also known as graphics pipeline or rendering pipeline.When the 3D model created for video game or any other 3D animation then the graphic pipeline process starts.As it turns 3D model into what computer displays.The steps are to be performed to process the graphic pipeline depends on the software or hardware and computer characteristics that are used.There is no universal case of graphic pipeline is introduce for all cases.Application programing interfaces (APIs) are used to unify similar steps and control graphics pipeline of given acceleration like Direct3D and OpenGL.This model is usually used in real time rendering. Q23) Short note on geometric modelling used in haptic rendering pipeline modelling in virtual reality.A23) Haptic rendering pipelines are the applied forces that are used by users through force feedback device.The difference between haptic device and input interfaces such as mouse and keyboard is that it will give the force feedback to the virtual environment.Haptic rendering is used to enable user to touch the, feel and manipulate virtual objects.It also enhance the virtual experience to the user.Following figure 7.4 shows the process of haptic rendering pipeline modelling which contains some stages.Collision detection stage Force computation stage Tactile computation stage
Fig. no. 7.4Following are some concepts that are used in Haptic Rendering Pipeline Modeling.Geometric ModelingIt is a modelling based on CAD file.It uses the AutoCAD softwareThe files needs to be converted to formats compatible with VR toolkit.This modelling is used in preexisting models in manufacturing applications.In this the each part is considered as separate file. Kinematic ModelingIt has homogeneous transformation matrices.It relates to the object system of coordinates to world system of coordinates given by homogeneous transformation matrix.If the virtual object moves the transformation matrix becomes a function of time.If the aligned virtual object translates all vertices gets translated.If the virtual object translates back to its initial position all its vertices translate by an equal but negative amount.It allows models to be partitioned into a hierarchy and become dynamic. Physical Modeling It uses the bounding bpx collision detection for fast response.There are two types of bounding boxes with fixed size or variable size.Fixed size is computationally faster but less precise.For more precise detection can use a two stage collision detection which followed by slower exact collision detection stage. Behavior Modeling.The behavior modelling having simulation level of autonomy (LOA) function of its components.There are three levels of autonomy as guided, programmed and autonomous.It has behavior independent of user’s input.This is needed in large virtual environment which is impossible fr user to provide all required inputs.
|
|
|
|
0 matching results found