UNIT 4

Trees

1. What are tree and its terminology?

• A Tree is a recursive data structure containing the set of one or more data nodes where one node is designated as the root of the tree while the remaining nodes are called as the children of the root.
• The nodes other than the root node are partitioned into the non empty sets where each one of them is to be called sub-tree.
• Nodes of a tree either maintain a parent-child relationship between them or they are sister nodes.
• In a general tree, A node can have any number of children nodes but it can have only a single parent.
• The following image shows a tree, where the node A is the root node of the tree while the other nodes can be seen as the children of A.

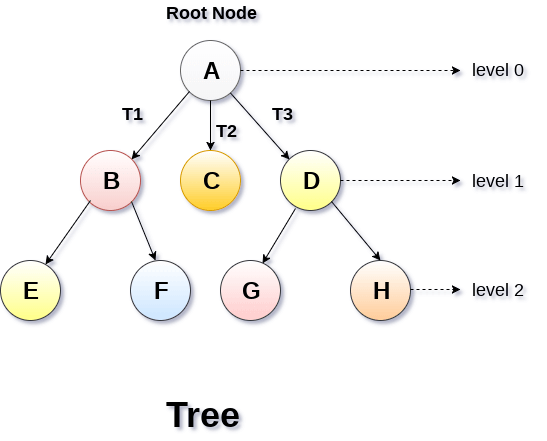
Basic terminology

• Root Node :- The root node is the topmost node in the tree hierarchy. In other words, the root node is the one which doesn't have any parent.
• Sub Tree :- If the root node is not null, the tree T1, T2 and T3 is called sub-trees of the root node.
• Leaf Node :- The node of tree, which doesn't have any child node, is called leaf node. Leaf node is the bottom most node of the tree. There can be any number of leaf nodes present in a general tree. Leaf nodes can also be called external nodes.
• Path :- The sequence of consecutive edges is called path. In the tree shown in the above image, path to the node E is A→ B → E.
• Ancestor node :- An ancestor of a node is any predecessor node on a path from root to that node. The root node doesn't have any ancestors. In the tree shown in the above image, the node F have the ancestors, B and A.
• Degree :- Degree of a node is equal to number of children, a node have. In the tree shown in the above image, the degree of node B is 2. Degree of a leaf node is always 0 while in a complete binary tree, degree of each node is equal to 2.
• Level Number :- Each node of the tree is assigned a level number in such a way that each node is present at one level higher than its parent. Root node of the tree is always present at level 0.

Static representation of tree

1. #define MAXNODE 500  
2. Struct treenode {  
3.    Int root;  
4.    Int father;  
5.    Int son;  
6.    Int next;   
7. }   

Dynamic representation of tree

1. Struct treenode   
2. {  
3.    Int root;  
4.    Struct treenode *father;   
5.    Struct treenode *son   
6.    Struct treenode *next;   
7. }  

2.     What are the Types of Tree?

The tree data structure can be classified into six different categories.

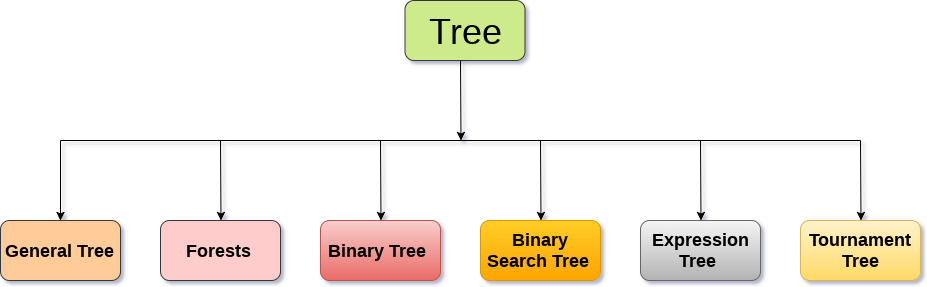
General Tree

General Tree stores the elements in a hierarchical order in which the top level element is always present at level 0 as the root element. All the nodes except the root node are present at number of levels. The nodes which are present on the same level are called siblings while the nodes which are present on the different levels exhibit the parent-child relationship among them. A node may contain any number of sub-trees. The tree in which each node contain 3 sub-tree, is called ternary tree.

Forests

Forest can be defined as the set of disjoint trees which can be obtained by deleting the root node and the edges which connects root node to the first level node.

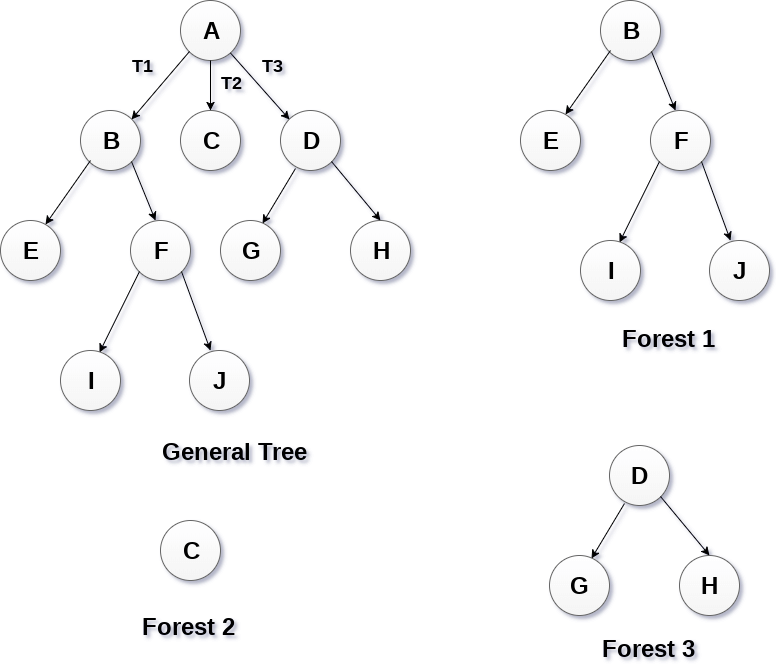
Binary Tree

Binary tree is a data structure in which each node can have at most 2 children. The node present at the top most level is called the root node. A node with the 0 children is called leaf node. Binary Trees are used in the applications like expression evaluation and many more. We will discuss binary tree in detail, later in this tutorial.

Binary Search Tree

Binary search tree is an ordered binary tree. All the elements in the left sub-tree are less than the root while elements present in the right sub-tree are greater than or equal to the root node element. Binary search trees are used in most of the applications of computer science domain like searching, sorting, etc.

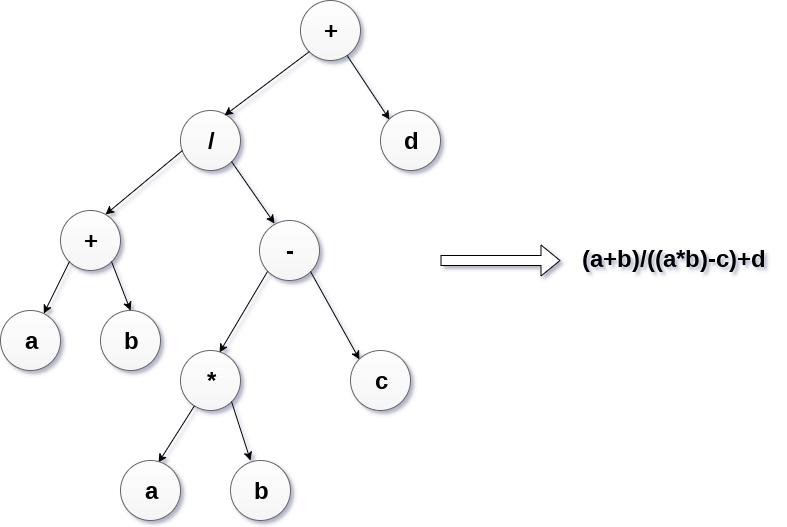
Expression Tree

Expression trees are used to evaluate the simple arithmetic expressions. Expression tree is basically a binary tree where internal nodes are represented by operators while the leaf nodes are represented by operands. Expression trees are widely used to solve algebraic expressions like (a+b)*(a-b). Consider the following example.

Q. Construct an expression tree by using the following algebraic expression.

(a + b) / (a*b - c) + d

Tournament Tree

Tournament tree are used to record the winner of the match in each round being played between two players. Tournament tree can also be called as selection tree or winner tree. External nodes represent the players among which a match is being played while the internal nodes represent the winner of the match played. At the top most level, the winner of the tournament is present as the root node of the tree.

For example, tree .of a chess tournament being played among 4 players is shown as follows. However, the winner in the left sub-tree will play against the winner of right sub-tree.

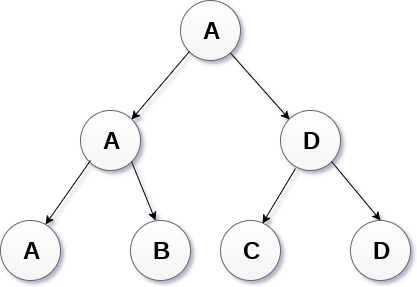
3.     Explain Binary Tree

Binary Tree is a special type of generic tree in which, each node can have at most two children. Binary tree is generally partitioned into three disjoint subsets.

1. Root of the node
2. Left sub-tree which is also a binary tree.
3. Right binary sub-tree

A binary Tree is shown in the following image.

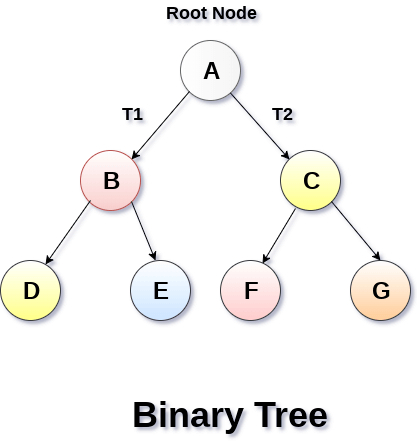
Types of Binary Tree

1. Strictly Binary Tree

In Strictly Binary Tree, every non-leaf node contain non-empty left and right sub-trees. In other words, the degree of every non-leaf node will always be 2. A strictly binary tree with n leaves, will have (2n - 1) nodes.

A strictly binary tree is shown in the following figure.

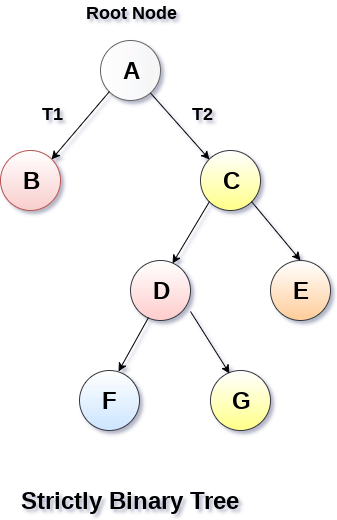
2. Complete Binary Tree

A Binary Tree is said to be a complete binary tree if all of the leaves are located at the same level d. A complete binary tree is a binary tree that contains exactly 2^l nodes at each level between level 0 and d. The total number of nodes in a complete binary tree with depth d is 2d+1-1 where leaf nodes are 2d while non-leaf nodes are 2d-1.

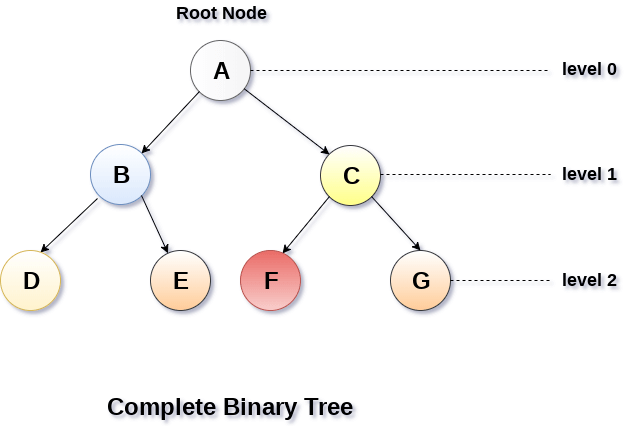
Binary Tree Traversal

4.     Explain Binary Tree representation

There are two types of representation of a binary tree:

1. Linked Representation

In this representation, the binary tree is stored in the memory, in the form of a linked list where the number of nodes are stored at non-contiguous memory locations and linked together by inheriting parent child relationship like a tree. Every node contains three parts : pointer to the left node, data element and pointer to the right node. Each binary tree has a root pointer which points to the root node of the binary tree. In an empty binary tree, the root pointer will point to null.

Consider the binary tree given in the figure below.

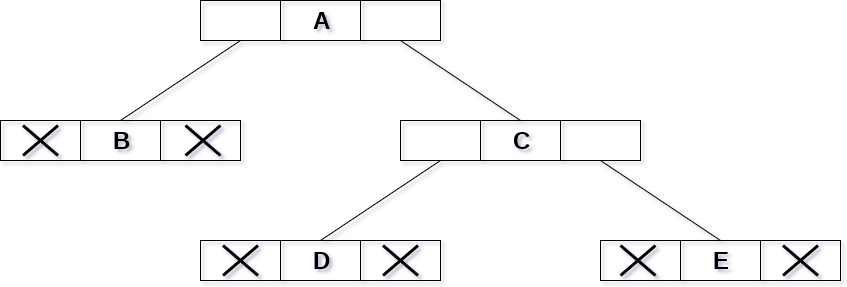
In the above figure, a tree is seen as the collection of nodes where each node contains three parts : left pointer, data element and right pointer. Left pointer stores the address of the left child while the right pointer stores the address of the right child. The leaf node contains null in its left and right pointers.

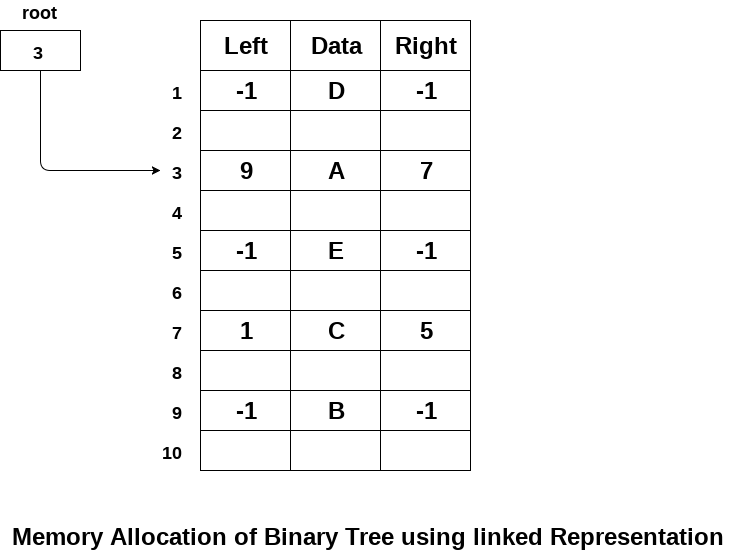
The following image shows about how the memory will be allocated for the binary tree by using linked representation. There is a special pointer maintained in the memory which points to the root node of the tree. Every node in the tree contains the address of its left and right child. Leaf node contains null in its left and right pointers.

2. Sequential Representation

This is the simplest memory allocation technique to store the tree elements but it is an inefficient technique since it requires a lot of space to store the tree elements. A binary tree is shown in the following figure along with its memory allocation.

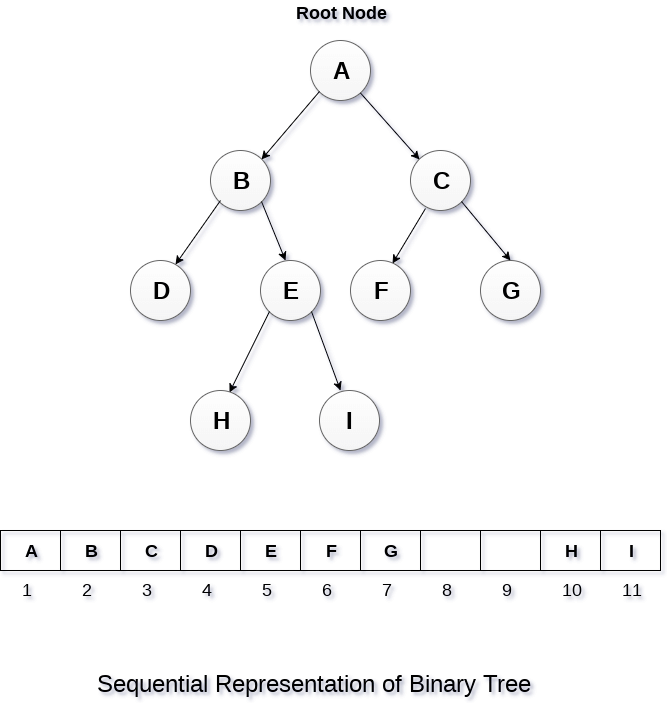
In this representation, an array is used to store the tree elements. Size of the array will be equal to the number of nodes present in the tree. The root node of the tree will be present at the 1st index of the array. If a node is stored at ith index then its left and right children will be stored at 2i and 2i+1 location. If the 1st index of the array i.e. tree[1] is 0, it means that the tree is empty.

Output

Infix expression is

a + b - e * f * g

6.     What are the Types of Binary Tree?

Strictly binary tree

Strictly binary tree is defined as a binary tree where all the nodes will have either zero or two children. It does not include one child in any node.

Skew tree

A skew tree is defined as a binary tree in which every node except the leaf has only one child node. There are two types of skew tree, i.e. left skewed binary tree and right skewed binary tree.

Left skewed binary tree

A left skew tree has node associated with only the left child. It is a binary tree contains only left subtrees.

Right skewed binary tree

A right skew tree has node associated with only the right child. It is a binary tree contains only right subtrees.

Full binary tree or proper binary tree

A binary tree is defined as a full binary tree if all leaves are at the same level and every non leaf node has exactly two children and it should consist of highest possible number of nodes in all levels. A full binary tree of height h has maximum 2h+1 – 1 nodes.

Complete binary tree

Every non leaf node has exactly two children but all leaves are not necessary to belong at the same level. A complete binary tree is defined as one where all levels have the highest number of nodes except the last level. The last level elements should be filled from left to right direction.

Almost complete binary tree

An almost complete binary tree is defined as a tree in which each node that has a right child also has a left child. Having a left child does not need a node to have a right child

7.     Differences between General Tree and Binary Tree

General Tree

• General tree has no limit of number of children.
• Evaluating any expression is hard in general trees.

Binary Tree

• A binary tree has maximum two children
• Evaluation of expression is simple in binary tree.

Application of trees

• Manipulation of arithmetic expression
• Construction of symbol table
• Analysis of Syntax
• Writing Grammar
• Creation of Expression Tree

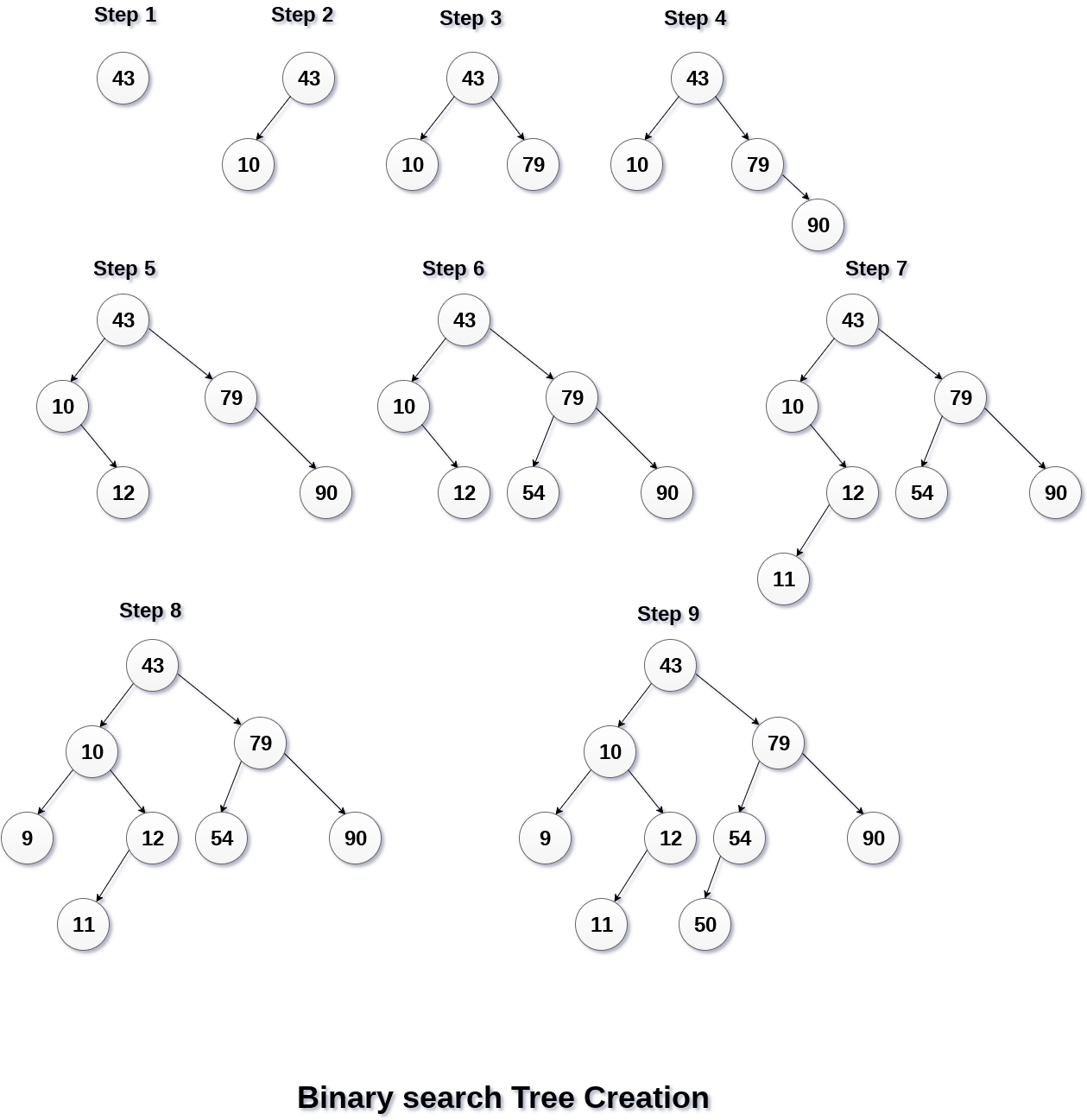
8.     Create the binary search tree using the following data elements.

43, 10, 79, 90, 12, 54, 11, 9, 50

1. Insert 43 into the tree as the root of the tree.
2. Read the next element, if it is lesser than the root node element, insert it as the root of the left sub-tree.
3. Otherwise, insert it as the root of the right of the right sub-tree.

The process of creating BST by using the given elements, is shown in the image below.

9.     What are the Operations on Binary Search Tree?

There are many operations which can be performed on a binary search tree.

10. Write a Program to implement BST operations

1. #include <iostream>  
2. #include <stdlib.h>  
3. Using namespace std;  
4. Struct Node {  
5.    Int data;  
6.    Node *left;  
7.    Node *right;  
8. };  
9. Node* create(int item)  
10. {  
11.    Node* node = new Node;  
12.    Node->data = item;  
13.    Node->left = node->right = NULL;  
14.    Return node;  
15. }  
16.  
17. Void inorder(Node *root)  
18. {  
19.    If (root == NULL)  
20.        Return;  
21.  
22.    Inorder(root->left);  
23.    Cout<< root->data << "   ";  
24.    Inorder(root->right);  
25. }  
26. Node* findMinimum(Node* cur)  
27. {  
28.    While(cur->left != NULL) {  
29.        Cur = cur->left;  
30.    }  
31.    Return cur;  
32. }  
33. Node* insertion(Node* root, int item)  
34. {  
35.    If (root == NULL)  
36.        Return create(item);  
37.    If (item < root->data)  
38.        Root->left = insertion(root->left, item);  
39.    Else  
40.        Root->right = insertion(root->right, item);  
41.  
42.    Return root;  
43. }  
44.  
45. Void search(Node* &cur, int item, Node* &parent)  
46. {  
47.    While (cur != NULL && cur->data != item)  
48.    {  
49.        Parent = cur;  
50.  
51.        If (item < cur->data)  
52.            Cur = cur->left;  
53.        Else  
54.            Cur = cur->right;  
55.    }  
56. }  
57.  
58. Void deletion(Node*& root, int item)  
59. {  
60.    Node* parent = NULL;  
61.    Node* cur = root;  
62.  
63.    Search(cur, item, parent);  
64.    If (cur == NULL)  
65.        Return;  
66.  
67.    If (cur->left == NULL && cur->right == NULL)  
68.    {  
69.        If (cur != root)  
70.        {  
71.            If (parent->left == cur)  
72.                Parent->left = NULL;  
73.            Else  
74.                Parent->right = NULL;  
75.        }  
76.        Else  
77.            Root = NULL;  
78.  
79.        Free(cur);       
80.    }  
81.    Else if (cur->left && cur->right)  
82.    {  
83.        Node* succ  = findMinimum(cur- >right);  
84.  
85.        Int val = succ->data;  
86.  
87.        Deletion(root, succ->data);  
88.  
89.        Cur->data = val;  
90.    }  
91.  
92.    Else  
93.    {  
94.        Node* child = (cur->left)? Cur- >left: cur->right;  
95.  
96.        If (cur != root)  
97.        {  
98.            If (cur == parent->left)  
99.                Parent->left = child;  
100.             Else  
101.                 Parent->right = child;  
102.         }  
103.   
104.         Else  
105.             Root = child;  
106.         Free(cur);  
107.     }  
108. }  
109.   
110. Int main()  
111. {  
112.    Node* root = NULL;  
113.    Int keys[8];  
114.    For(int i=0;i<8;i++)  
115.     {  
116.     Cout << "Enter value to be inserted";  
117.     Cin>>keys[i];  
118.         Root = insertion(root, keys[i]);  
119.     }  
120.   
121.     Inorder(root);  
122.     Cout<<"\n";  
123.     Deletion(root, 10);  
124.     Inorder(root);  
125.     Return 0;  
126. }  

Output:

Enter value to be inserted? 10

Enter value to be inserted? 20

Enter value to be inserted? 30

Enter value to be inserted? 40

Enter value to be inserted?  5

Enter value to be inserted? 25

Enter value to be inserted? 15

Enter value to be inserted?  5

55101520253040

551520253040