UNIT 6
Hashing and File Organization
- Explain Hashing
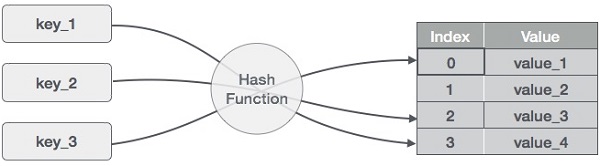
Hashing is a technique to convert a range of key values into a range of indexes of an array. We're going to use modulo operator to get a range of key values. Consider an example of hash table of size 20, and the following items are to be stored. Item are in the (key,value) format.
- (1,20)
- (2,70)
- (42,80)
- (4,25)
- (12,44)
- (14,32)
- (17,11)
- (13,78)
- (37,98)
Sr.No. | Key | Hash | Array Index |
1 | 1 | 1 % 20 = 1 | 1 |
2 | 2 | 2 % 20 = 2 | 2 |
3 | 42 | 42 % 20 = 2 | 2 |
4 | 4 | 4 % 20 = 4 | 4 |
5 | 12 | 12 % 20 = 12 | 12 |
6 | 14 | 14 % 20 = 14 | 14 |
7 | 17 | 17 % 20 = 17 | 17 |
8 | 13 | 13 % 20 = 13 | 13 |
9 | 37 | 37 % 20 = 17 | 17 |
2. What is Linear Probing?
As we can see, it may happen that the hashing technique is used to create an already used index of the array. In such a case, we can search the next empty location in the array by looking into the next cell until we find an empty cell. This technique is called linear probing.
Sr.No. | Key | Hash | Array Index | After Linear Probing, Array Index |
1 | 1 | 1 % 20 = 1 | 1 | 1 |
2 | 2 | 2 % 20 = 2 | 2 | 2 |
3 | 42 | 42 % 20 = 2 | 2 | 3 |
4 | 4 | 4 % 20 = 4 | 4 | 4 |
5 | 12 | 12 % 20 = 12 | 12 | 12 |
6 | 14 | 14 % 20 = 14 | 14 | 14 |
7 | 17 | 17 % 20 = 17 | 17 | 17 |
8 | 13 | 13 % 20 = 13 | 13 | 13 |
9 | 37 | 37 % 20 = 17 | 17 | 18 |
3. Explain Search Operation of hash table
Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.
Example
Struct DataItem *search(int key) {
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] != NULL) {
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
4. Explain Insert Operation of hash table
Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code.
Example
Void insert(int key,int data) {
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
5. Explain Delete Operation of hash table
Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact.
Example
Struct DataItem* delete(struct DataItem* item) {
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL) {
if(hashArray[hashIndex]->key == key) {
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
Hash Table is a data structure which stores data in an associative manner. In hash table, the data is stored in an array format where each data value has its own unique index value. Access of data becomes very fast, if we know the index of the desired data.
6. Explain Searching Techniques of hash table
In data structures,
- There are several searching techniques like linear search, binary search, search trees etc.
- In these techniques, time taken to search any particular element depends on the total number of elements.
Example-
- Linear search takes O(n) time to perform the search in unsorted arrays consisting of n elements.
- Binary Search takes O(logn) time to perform the search in sorted arrays consisting of n elements.
- It takes O(logn) time to perform the search in BST consisting of n elements.
Drawback-
The main drawback of these techniques is-
- As the number of elements increases, time taken to perform the search also increases.
- This becomes problematic when total number of elements become too large.
Hashing in Data Structure-
In data structures,
- Hashing is a well-known technique to search any particular element among several elements.
- It minimizes the number of comparisons while performing the search.
Advantage-
Unlike other searching techniques,
- Hashing is extremely efficient.
- The time taken by it to perform the search does not depend upon the total number of elements.
- It completes the search with constant time complexity O(1).
7. What are the Types of Hash Functions?
There are various types of hash functions available such as-
- Mid Square Hash Function
- Division Hash Function
- Folding Hash Function etc
It depends on the user which hash function he wants to use.
Properties of Hash Function-
The properties of a good hash function are-
- It is efficiently computable.
- It minimizes the number of collisions.
- It distributes the keys uniformly over the table.
8. What are the Characteristics of Good Hash Function?
- The hash value is fully determined by the data being hashed.
- The hash Function uses all the input data.
- The hash function "uniformly" distributes the data across the entire set of possible hash values.
- The hash function generates complicated hash values for similar strings.
Some Popular Hash Function is:
1. Division Method:
Choose a number m smaller than the number of n of keys in k (The number m is usually chosen to be a prime number or a number without small divisors, since this frequently a minimum number of collisions).
The hash function is:

For Example: if the hash table has size m = 12 and the key is k = 100, then h (k) = 4. Since it requires only a single division operation, hashing by division is quite fast.
2. Multiplication Method:
The multiplication method for creating hash functions operates in two steps. First, we multiply the key k by a constant A in the range 0 < A < 1 and extract the fractional part of kA. Then, we increase this value by m and take the floor of the result.
The hash function is:

Where "k A mod 1" means the fractional part of k A, that is, k A -⌊k A⌋.
3. Mid Square Method:
The key k is squared. Then function H is defined by
- H (k) = L
Where L is obtained by deleting digits from both ends of k2. We emphasize that the same position of k2 must be used for all of the keys.
4. Folding Method:
The key k is partitioned into a number of parts k1, k2.... kn where each part except possibly the last, has the same number of digits as the required address.
Then the parts are added together, ignoring the last carry.
H (k) = k1+ k2+.....+kn
Example: Company has 68 employees, and each is assigned a unique four- digit employee number. Suppose L consist of 2- digit addresses: 00, 01, and 02....99. We apply the above hash functions to each of the following employee numbers:
- 3205, 7148, 2345
(a) Division Method: Choose a Prime number m close to 99, such as m =97, Then
- H (3205) = 4, H (7148) = 67, H (2345) = 17.
That is dividing 3205 by 17 gives a remainder of 4, dividing 7148 by 97 gives a remainder of 67, dividing 2345 by 97 gives a remainder of 17.
(b) Mid-Square Method:
k = 3205 7148 2345
k2= 10272025 51093904 5499025
h (k) = 72 93 99
Observe that fourth & fifth digits, counting from right are chosen for hash address.
(c) Folding Method: Divide the key k into 2 parts and adding yields the following hash address:
- H (3205) = 32 + 50 = 82 H (7148) = 71 + 84 = 55
- H (2345) = 23 + 45 = 68
9. Why we need Hashing?
Suppose we have 50 employees, and we have to give 4 digit key to each employee (as for security), and we want after entering a key, direct user map to a particular position where data is stored.
If we give the location number according to 4 digits, we will have to reserve 0000 to 9999 addresses because anybody can use anyone as a key. There is a lot of wastage.
In order to solve this problem, we use hashing which will produce a smaller value of the index of the hash table corresponding to the key of the user.
Universal Hashing
Let H be a finite collection of hash functions that map a given universe U of keys into the range {0, 1..... m-1}. Such a collection is said to be universal if for each pair of distinct keys k,l∈U, the number of hash functions h∈ H for which h(k)= h(l) is at most |H|/m. In other words, with a hash function randomly chosen from H, the chance of a collision between distinct keys k and l is no more than the chance 1/m of a collision if h(k) and h(l)were randomly and independently chosen from the set {0,1,...m-1}.
Rehashing
If any stage the hash table becomes nearly full, the running time for the operations of will start taking too much time, insert operation may fail in such situation, the best possible solution is as follows:
- Create a new hash table double in size.
- Scan the original hash table, compute new hash value and insert into the new hash table.
- Free the memory occupied by the original hash table.
10. PRACTICE PROBLEM BASED ON SEPARATE CHAINING-
Problem-
Using the hash function ‘key mod 7’, insert the following sequence of keys in the hash table-
50, 700, 76, 85, 92, 73 and 101
Use separate chaining technique for collision resolution.
Solution-
The given sequence of keys will be inserted in the hash table as-
Step-01:
- Draw an empty hash table.
- For the given hash function, the possible range of hash values is [0, 6].
- So, draw an empty hash table consisting of 7 buckets as-

Step-02:
- Insert the given keys in the hash table one by one.
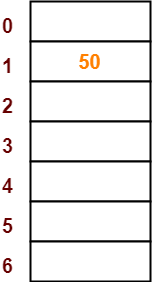
- The first key to be inserted in the hash table = 50.
- Bucket of the hash table to which key 50 maps = 50 mod 7 = 1.
- So, key 50 will be inserted in bucket-1 of the hash table as-
Step-03
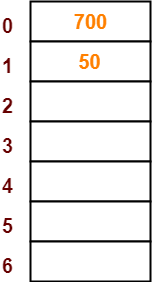
- The next key to be inserted in the hash table = 700.
- Bucket of the hash table to which key 700 maps = 700 mod 7 = 0.
- So, key 700 will be inserted in bucket-0 of the hash table as-
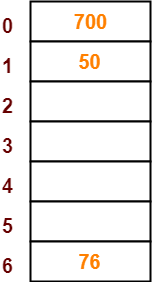
Step-04:
- The next key to be inserted in the hash table = 76.
- Bucket of the hash table to which key 76 maps = 76 mod 7 = 6.
- So, key 76 will be inserted in bucket-6 of the hash table as-
Step-05:
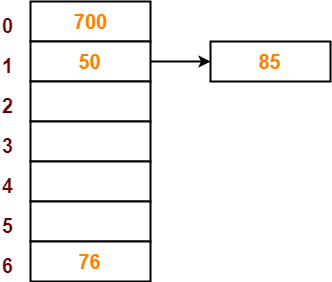
- The next key to be inserted in the hash table = 85.
- Bucket of the hash table to which key 85 maps = 85 mod 7 = 1.
- Since bucket-1 is already occupied, so collision occurs.
- Separate chaining handles the collision by creating a linked list to bucket-1.
- So, key 85 will be inserted in bucket-1 of the hash table as-
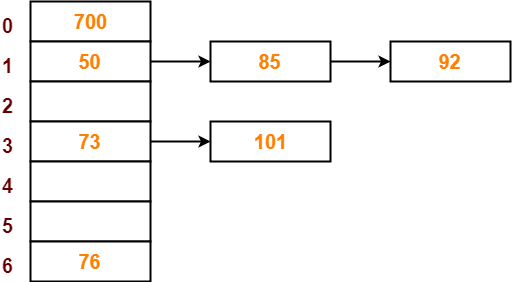
Step-06:
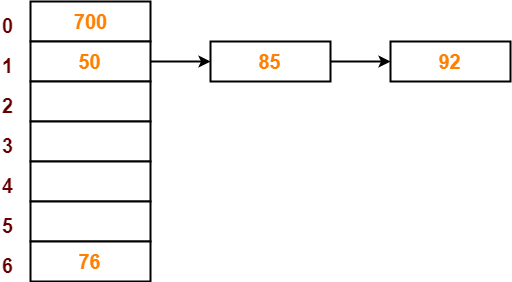
- The next key to be inserted in the hash table = 92.
- Bucket of the hash table to which key 92 maps = 92 mod 7 = 1.
- Since bucket-1 is already occupied, so collision occurs.
- Separate chaining handles the collision by creating a linked list to bucket-1.
- So, key 92 will be inserted in bucket-1 of the hash table as-
Step-07:
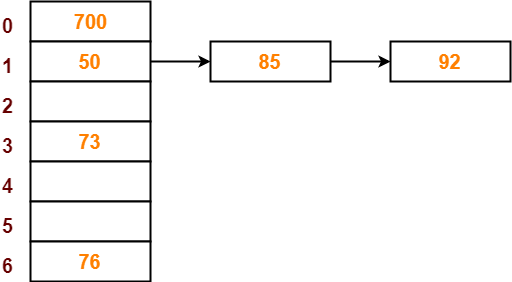
- The next key to be inserted in the hash table = 73.
- Bucket of the hash table to which key 73 maps = 73 mod 7 = 3.
- So, key 73 will be inserted in bucket-3 of the hash table as-
Step-08:
- The next key to be inserted in the hash table = 101.
- Bucket of the hash table to which key 101 maps = 101 mod 7 = 3.
- Since bucket-3 is already occupied, so collision occurs.
- Separate chaining handles the collision by creating a linked list to bucket-3.
- So, key 101 will be inserted in bucket-3 of the hash table as-